天津市和平区2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2023-11-24 类型:期中考试
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合题目要求的)
-
1. 我国古代数学的许多创新与发明都曾在世界上有重要影响.下列图形“杨辉三角”“中国七巧板”“刘微割圆术”“赵爽弦图”中,中心对称图形是( ).A、
 B、
B、 C、
C、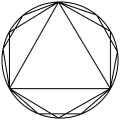 D、
D、 2. 若 , 是一元二次方程的两个根,则的值为( )A、 B、4 C、 D、33. 二次函数的开口方向、对称轴和顶点坐标分别为( )A、向下、直线、 B、向下、直线、 C、向下、直线、 D、向上、直线、4. 已知的半径为 , , 则点和的位置关系是( )A、点在圆上 B、点在圆外 C、点在圆内 D、不确定5. 把抛物线y=- x2向下平移1个单位长度,再向左平移1个单位长度,得到的抛物线解析式为( )A、y=- (x+1)2+1 B、y=- (x+1)2-1 C、y=- (x-1)2+ 1 D、y=- (x-1)2-16. 用配方法解一元二次方程时,首先把化成(a、b为常数)的形式,则的值为( )A、8 B、11 C、14 D、177. 如图,要设计一幅宽 , 长的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为 . 如果要使彩条所占面积是图案面积的三分之一,应如何设计彩条的宽度?
2. 若 , 是一元二次方程的两个根,则的值为( )A、 B、4 C、 D、33. 二次函数的开口方向、对称轴和顶点坐标分别为( )A、向下、直线、 B、向下、直线、 C、向下、直线、 D、向上、直线、4. 已知的半径为 , , 则点和的位置关系是( )A、点在圆上 B、点在圆外 C、点在圆内 D、不确定5. 把抛物线y=- x2向下平移1个单位长度,再向左平移1个单位长度,得到的抛物线解析式为( )A、y=- (x+1)2+1 B、y=- (x+1)2-1 C、y=- (x-1)2+ 1 D、y=- (x-1)2-16. 用配方法解一元二次方程时,首先把化成(a、b为常数)的形式,则的值为( )A、8 B、11 C、14 D、177. 如图,要设计一幅宽 , 长的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为 . 如果要使彩条所占面积是图案面积的三分之一,应如何设计彩条的宽度?若设每个横彩条的宽度为 , 则每个竖彩条的宽度为 , 则根据题意,列方程为( )
 A、 B、 C、 D、8. 如图,是的直径,分别以点O和点B为圆心,大于的长为半径作弧(弧所在圆的半径都相等),两弧相交于M , N两点,直线与相交于C , D两点,若 , 则的长为( )
A、 B、 C、 D、8. 如图,是的直径,分别以点O和点B为圆心,大于的长为半径作弧(弧所在圆的半径都相等),两弧相交于M , N两点,直线与相交于C , D两点,若 , 则的长为( ) A、 B、4 C、 D、9. 如图,是绕点顺时针旋转得到的,延长与相交于点、若 , , , 则的度数为( )
A、 B、4 C、 D、9. 如图,是绕点顺时针旋转得到的,延长与相交于点、若 , , , 则的度数为( )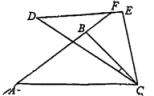 A、 B、 C、 D、10. 如图,等边的边长为 , 点从点出发在 , 边上运动,当点运动到点后停止运动.过作边的垂线,交于 , 用表示线段的长度,的面积是线段长度的函数,则与的函数图象正确的是( )
A、 B、 C、 D、10. 如图,等边的边长为 , 点从点出发在 , 边上运动,当点运动到点后停止运动.过作边的垂线,交于 , 用表示线段的长度,的面积是线段长度的函数,则与的函数图象正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、 11. 如图,都是的半径, , 则下列结论不正确的是( )
11. 如图,都是的半径, , 则下列结论不正确的是( )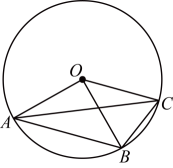 A、 B、 C、 D、12. 已知抛物线(a , b , c是常数,)经过点 , , 有下列结论:
A、 B、 C、 D、12. 已知抛物线(a , b , c是常数,)经过点 , , 有下列结论:①图象的对称轴为直线;
②若一元二次方程的两个根是 , , 则 , ;
③若 , 则;
④无论x取何值,代数式的值都大于0.
其中,正确结论的个数是( )
A、1 B、2 C、3 D、4二、填空题(本大题共6小题,每小题3分,共18分)
-
13. 点关于原点对称点的坐标为 .14. 如图,五角星围绕中心旋转,至少旋转(度)能与自身重合.
 15. 飞机着陆后滑行的距离s(单位:)关于滑行的时间t(单位:)的函数解析式 , 飞机着陆后滑行米才能停下来.16. 若方程x2-4084441=0的两根为±2021,则方程x2-2x-4084440=0的两根为 .17. 如图,在四边形中, , 点E在线段上运动,点F在线段上, , 则线段的最小值为 .
15. 飞机着陆后滑行的距离s(单位:)关于滑行的时间t(单位:)的函数解析式 , 飞机着陆后滑行米才能停下来.16. 若方程x2-4084441=0的两根为±2021,则方程x2-2x-4084440=0的两根为 .17. 如图,在四边形中, , 点E在线段上运动,点F在线段上, , 则线段的最小值为 . 18. 如图,在每个小正方形的边长为1的网格中,内接于圆,且顶点A , B均在格点上,点C在网格线上.
18. 如图,在每个小正方形的边长为1的网格中,内接于圆,且顶点A , B均在格点上,点C在网格线上. (1)、线段的长等于;(2)、请用无刻度的直尺,在如图所示的网格中,在圆上画出点D , 使平分(不要求证明,保留作图痕迹)
(1)、线段的长等于;(2)、请用无刻度的直尺,在如图所示的网格中,在圆上画出点D , 使平分(不要求证明,保留作图痕迹)三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤或推理过程).
-
19.(1)、解一元二次方程:;(2)、已知关于x的一元二次方程有两个不相等的实数根 , .
①求k的取值范围;
②若 (填序号),求k的值.
请同学们从①;②;③中选择一个作为条件,补充完整题目,并完成解答.
20. 一个滑雪者从山坡滑下,为了得出滑行距离s(单位:m)与滑行时间t(单位:s)之间的关系式,在滑道上设置了几个固定的计时点,测得一些数据(如表格).为观察s与t之间的关系,建立坐标系,以t为横坐标,s为纵坐标,描出表中数据对应的点(如图).可以看出,其中绝大部分的点都近似的位于某条抛物线上.于是,我们用二次函数来近似的表示s与t的关系.
 (1)、在位置①处,当时, , 所以;(2)、有一个计时点的计时装置出现了故障,请同学们用平滑曲线连接这些绝大部分的点 , 通过观察发现故障点的位置编号可能是;(3)、利用函数图象推测当此滑雪者滑行距离为30m时,用时约为s(结果保留一位小数);(4)、求s与t的函数关系式,并求出滑雪者在故障位置的滑行距离.21. 如图,四边形内接于 , 连接 , , .
(1)、在位置①处,当时, , 所以;(2)、有一个计时点的计时装置出现了故障,请同学们用平滑曲线连接这些绝大部分的点 , 通过观察发现故障点的位置编号可能是;(3)、利用函数图象推测当此滑雪者滑行距离为30m时,用时约为s(结果保留一位小数);(4)、求s与t的函数关系式,并求出滑雪者在故障位置的滑行距离.21. 如图,四边形内接于 , 连接 , , .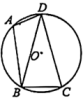 (1)、求的大小;(2)、若的半径为3,求的长.22. 已知,是直径,半径经过弦的中点 .
(1)、求的大小;(2)、若的半径为3,求的长.22. 已知,是直径,半径经过弦的中点 .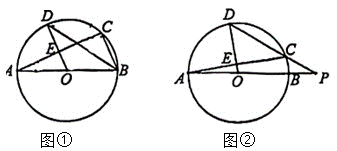 (1)、如图①,连接 , , 若 , 求和的大小;(2)、如图②,连接并延长交的延长线于点 , 若 , 求的大小.23. 2023年杭州亚运会胜利闭幕.本次亚运会中国代表团共获得383枚奖牌,位居奖牌榜第一,创造了新的历史.在亚运会期间,买一件印有亚运会元素的T恤去看比赛,成为了体育迷们的“仪式感”.某商店以每件40元的价格购进一批这样的T恤,以每件60元的价格出售.经统计,4月份的销售量为192件,6月份的销售量为300件.(1)、求该款T恤4月份到6月份销售量的月平均增长率;(2)、从7月份起,商场决定采用降价促销回馈顾客,销售利润不超过30%.经试验,发现该款T恤在6月份销售量的基础上,每降价1元,月销售量就会增加20件.如何定价才能使利润最大?并求出最大利润是多少元?24. 已知矩形 , , , 将矩形绕A顺时针旋转 , 得到矩形 , 点B的对应点是点E , 点C的对应点是点F , 点D的对应点是点G .
(1)、如图①,连接 , , 若 , 求和的大小;(2)、如图②,连接并延长交的延长线于点 , 若 , 求的大小.23. 2023年杭州亚运会胜利闭幕.本次亚运会中国代表团共获得383枚奖牌,位居奖牌榜第一,创造了新的历史.在亚运会期间,买一件印有亚运会元素的T恤去看比赛,成为了体育迷们的“仪式感”.某商店以每件40元的价格购进一批这样的T恤,以每件60元的价格出售.经统计,4月份的销售量为192件,6月份的销售量为300件.(1)、求该款T恤4月份到6月份销售量的月平均增长率;(2)、从7月份起,商场决定采用降价促销回馈顾客,销售利润不超过30%.经试验,发现该款T恤在6月份销售量的基础上,每降价1元,月销售量就会增加20件.如何定价才能使利润最大?并求出最大利润是多少元?24. 已知矩形 , , , 将矩形绕A顺时针旋转 , 得到矩形 , 点B的对应点是点E , 点C的对应点是点F , 点D的对应点是点G . (1)、如图①;当时,连接 , 求的长;(2)、如图②,当边经过点D时,延长交于点P , 求的长;(3)、连接 , 点M是的中点,连接 , 在旋转过程中,线段的最大值 .25. 已知抛物线( , , 是常数,)的顶点为 , 与轴相交于 , 两点(点在点的左侧),与轴相交于点 .(1)、若点 , 求点和点的坐标;(2)、将点绕点逆时针方向旋转 , 点的对应点为 , 若 , 两点关于点中心对称,求点的坐标和抛物线解析式:(3)、在(1)的条件下,点为直线下方抛物线上的一个动点,过点作轴,与相交于点 , 过点作轴,与轴相交于点 , 求的最大值及此时点的坐标.
(1)、如图①;当时,连接 , 求的长;(2)、如图②,当边经过点D时,延长交于点P , 求的长;(3)、连接 , 点M是的中点,连接 , 在旋转过程中,线段的最大值 .25. 已知抛物线( , , 是常数,)的顶点为 , 与轴相交于 , 两点(点在点的左侧),与轴相交于点 .(1)、若点 , 求点和点的坐标;(2)、将点绕点逆时针方向旋转 , 点的对应点为 , 若 , 两点关于点中心对称,求点的坐标和抛物线解析式:(3)、在(1)的条件下,点为直线下方抛物线上的一个动点,过点作轴,与相交于点 , 过点作轴,与轴相交于点 , 求的最大值及此时点的坐标.