专题03 函数的性质综合-2024年高考数学二轮重难点精练
试卷更新日期:2023-11-23 类型:二轮复习
一、选择题
-
1. 下列函数中,既是偶函数又在区间上单调递增的函数是( )A、 B、 C、 D、2. 已知定义在上的偶函数 , 其导函数为 , 若 , , 则不等式的解集是( )A、 B、 C、 D、3. 已知符号函数 , 偶函数满足 , 当时, , 则( )A、 B、 C、 D、4. 已知函数 , 则不等式的解集是( )A、 B、 C、 D、5. 已知函数是定义在上的奇函数, , 当时, , 则( )A、 B、 C、2 D、36. 函数的大致图象是( ).A、
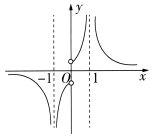 B、
B、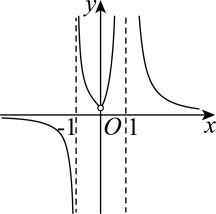 C、
C、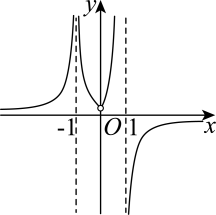 D、
D、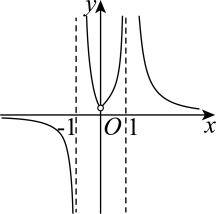 7. 已知函数 , 若 , 则实数的取值范围为( )A、 B、 C、 D、8. 已知的图象如图,则的解析式可能是( )
7. 已知函数 , 若 , 则实数的取值范围为( )A、 B、 C、 D、8. 已知的图象如图,则的解析式可能是( ) A、 B、 C、 D、9. 已知定义域为的函数满足 , 且在区间上还满足:①当时,都有;②;③.则等于( )A、 B、 C、1 D、10. 已知函数满足 , 且是偶函数,当时, , 则( )A、 B、3 C、 D、11. 函数的图像大致为( )A、
A、 B、 C、 D、9. 已知定义域为的函数满足 , 且在区间上还满足:①当时,都有;②;③.则等于( )A、 B、 C、1 D、10. 已知函数满足 , 且是偶函数,当时, , 则( )A、 B、3 C、 D、11. 函数的图像大致为( )A、 B、
B、 C、
C、 D、
D、 12. 已知函数 , 则( )A、为奇函数 B、为偶函数 C、为奇函数 D、为偶函数13. 函数的图象可能为( )A、
12. 已知函数 , 则( )A、为奇函数 B、为偶函数 C、为奇函数 D、为偶函数13. 函数的图象可能为( )A、 B、
B、 C、
C、 D、
D、 14. 定义在上的函数满足 , 且为奇函数,则( )A、-2023 B、-2022 C、2022 D、202315. 设函数在定义域上满足 , 若在上是减函数,且 , 则不等式的解集为( )A、 B、 C、 D、16. 已知偶函数与其导函数的定义域均为 , 且也是偶函数,若 , 则实数的取值范围是( )A、 B、 C、 D、17. 已知函数同时满足性质:①;②当时, , 则函数可能为( )A、 B、 C、 D、18. 已知函数的定义域为 , 且是奇函数,是偶函数,设函数 . 若对任意恒成立,则实数的最大值为( )A、 B、 C、 D、19. 定义域为的函数满足 , 且对于任意均有 , 则( )A、 B、 C、 D、20. 若函数的定义域为 , 如果对中的任意一个 , 都有 , 且 , 则称函数为“类奇函数”.若某函数是“类奇函数”,则下列命题中,错误的是( )A、若0在定义域中,则 B、若 , 则 C、若在上单调递增,则在上单调递减 D、若定义域为 , 且函数也是定义域为的“类奇函数”,则函数也是“类奇函数”21. “家在花园里,城在山水间.半城山色半城湖,美丽惠州和谐家园......”首婉转动听的《美丽惠州》唱出了惠州的山姿水色和秀美可人的城市环境.下图1是惠州市风景优美的金山湖片区地图,其形状如一颗爱心.图2是由此抽象出来的一个“心形”图形,这个图形可看作由两个函数的图象构成,则“心形”在轴上方的图象对应的函数解析式可能为( )
14. 定义在上的函数满足 , 且为奇函数,则( )A、-2023 B、-2022 C、2022 D、202315. 设函数在定义域上满足 , 若在上是减函数,且 , 则不等式的解集为( )A、 B、 C、 D、16. 已知偶函数与其导函数的定义域均为 , 且也是偶函数,若 , 则实数的取值范围是( )A、 B、 C、 D、17. 已知函数同时满足性质:①;②当时, , 则函数可能为( )A、 B、 C、 D、18. 已知函数的定义域为 , 且是奇函数,是偶函数,设函数 . 若对任意恒成立,则实数的最大值为( )A、 B、 C、 D、19. 定义域为的函数满足 , 且对于任意均有 , 则( )A、 B、 C、 D、20. 若函数的定义域为 , 如果对中的任意一个 , 都有 , 且 , 则称函数为“类奇函数”.若某函数是“类奇函数”,则下列命题中,错误的是( )A、若0在定义域中,则 B、若 , 则 C、若在上单调递增,则在上单调递减 D、若定义域为 , 且函数也是定义域为的“类奇函数”,则函数也是“类奇函数”21. “家在花园里,城在山水间.半城山色半城湖,美丽惠州和谐家园......”首婉转动听的《美丽惠州》唱出了惠州的山姿水色和秀美可人的城市环境.下图1是惠州市风景优美的金山湖片区地图,其形状如一颗爱心.图2是由此抽象出来的一个“心形”图形,这个图形可看作由两个函数的图象构成,则“心形”在轴上方的图象对应的函数解析式可能为( )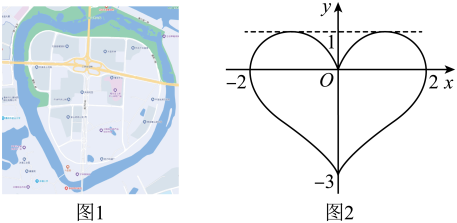 A、 B、 C、 D、
A、 B、 C、 D、二、多项选择题
-
22. 已知函数 , 且 , , 则下列结论正确的是( )A、 B、 C、在上单调递减 D、最小值为23. 已知函数 , 则下列说法中正确的是( )A、函数的图象关于原点对称 B、函数的图象关于轴对称 C、函数在上是减函数 D、函数的值域为24. 已知 , 则下列说法正确的是( )A、是周期函数 B、有对称轴 C、有对称中心 D、在上单调递增25. 已知函数的定义域是( , ),值域为 , 则满足条件的整数对可以是( )A、 B、 C、 D、26. 定义在上的函数满足 , 且当时, , 则( )A、 B、的一个周期为3 C、在上单调递增 D、27. 已知函数与及其导函数与的定义域均为 , 是偶函数,的图象关于点对称,则( )A、 B、 C、 D、28. 定义在上的函数满足如下条件:当时,则下列结论中正确的是( )A、 B、 C、在上单调递增 D、不等式的解集为29. 若定义在上的函数满足 , 且当时, , 则下列结论正确的是( ).A、若 , , , 则 B、若 , 则 C、若 , 则的图像关于点对称 D、若 , 则30. 已知函数 , 则( )A、 B、的最小值为 C、的最小值为 D、在区间上单调递增
三、填空题