广东省深圳市龙华区2023-2024学年七年级（上）数学期中试卷

试卷更新日期：2023-11-22 类型：期中考试

进入出卷网下载

一、选择题：本大题共10小题，.每小题3分，共30分。每小题只有一个选项符合题目要求。

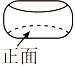
1. ﹣2023的相反数是（）

A、 $- \frac{1}{2023}$ B、﹣2023 C、 $\frac{1}{2023}$ D、2023

查看试题解析
2. “力箭一号”（ZK﹣1A）运载火箭在酒泉卫星发射中心采用“一箭六星”的方式，成功将六颗卫星送入预定轨道，首次飞行任务取得圆满成功．把卫星看成点，则卫星在预定轨道飞行留下的痕迹体现了（）

A、点动成线 B、线动成面 C、面动成体 D、面面相交成线

查看试题解析
3. 先贤孔子曾说过“鼓之舞之”，这是“鼓舞”一词最早的起源，如图是鼓的立体图形，该立体图形的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 手机信号的强弱通常采用负数来表示，绝对值越小表示信号越强（单位：dBm），则下列信号最强的是（）

A、﹣50 B、﹣60 C、﹣70 D、﹣80

查看试题解析
5. 一个物体的外形是长方体，其内部构造不详．用一组水平的平面截这个物体时，得到了一组（自下而上）截面，截面形状如图所示，这个长方体的内部构造可能是（）

A、圆柱 B、棱柱 C、棱锥 D、圆锥

查看试题解析
6. 规定a△b＝a+b﹣|﹣3|，则（﹣4）△2的值为（）

A、﹣5 B、1 C、9 D、﹣3

查看试题解析
7. 若代数式x﹣2y+8的值为18，则代数式3x﹣6y+4的值为（）

A、30 B、﹣26 C、﹣30 D、34

查看试题解析
8. 时差的计算方法：两个时区标准时间（即时区数）相减就是时差，时区的数值大的时间早．比如中国北京是东八区（+8），美国纽约是西五区（﹣5），两地的时差是13小时，北京比纽约要早13个小时，如北京时间2月1日18：00时，美国纽约为2月1日5：00．若美国纽约时间为3月1日20：00时，埃及开罗时间为3月2日3：00，则开罗所在的时区是（）

A、西二区 B、西三区 C、东二区 D、东三区

查看试题解析
9. 如图所示，直径为单位1的圆从原点沿着数轴无滑动的逆时针滚动一周到达A点，则A点表示的数是（）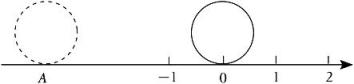

A、﹣2π B、﹣1+π C、﹣1+2π D、﹣π

查看试题解析
10. 如图是长为a ，宽为b的小长方形卡片，把六张这样的小长方形卡片不重叠地放在一个底面为长方形（长为8，宽为6）的盒子底部（如图），盒子底部未被卡片覆盖的部分用阴影表示，则两块阴影部分的周长之和为（）

A、16 B、24 C、20 D、28

查看试题解析

二、填空题（本大题共5小题，每小题3分，共15分）

11. 习近平总书记指出“善于学习，就是善于进步”．“国家中小学智慧云平台”上线的某天，全国大约有5450000人在平台上学习，将这个数据用科学记数法表示为．

查看试题解析
12. 某正方体的每个面上都有一个汉字，如图是它的一种展开图，那么在原正方体中，与“点”字所在面相对面上的汉字是．

查看试题解析
13. 两个互为相反数的数（0除外）的商是．

查看试题解析
14. 若x^my²与﹣x³yⁿ的和为0，则mn＝．

查看试题解析
15. 如图所示的运算程序中，若开始输入的x值为100，我们发现第1次输出的结果为50，第2次输出的结果为25，…，第2022次输出的结果为．

查看试题解析

三、解答题（本大题共7小题，共55分）》

16. 计算：

(1)、23﹣（﹣7）+（﹣16）；

(2)、（﹣4） $\div \frac{3}{4}$ ×（﹣3）；

(3)、﹣1⁴﹣6×（ $\frac{1}{2} - \frac{1}{3}$ ）．

查看试题解析
17. 先化简再求值：3（a²b+ab²）﹣2（a²b﹣1）﹣2ab²﹣2，其中a＝﹣1，b＝2．

查看试题解析
18. 如图是由一些棱长都为1cm的小正方体组合成的简单几何体．

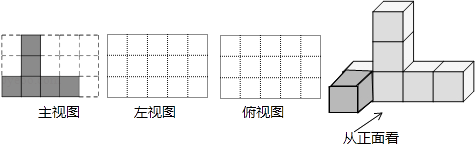(1)、该几何体的主视图如图所示，请在下面方格纸中分别画出它的左视图和俯视图；

(2)、如果在这个几何体上再添加一些小正方体，并保持俯视图和左视图不变，最多可以再添加块小正方体．

查看试题解析
19. 某中学一教室前有一块长为12米，宽为4x米的长方形空地，学校向全校师生征集这块地的绿化设计方案并要求绿地面积大于这块地总面积的 $\frac{5}{8}$ ，如图是学生小明的设计方案，阴影部分是绿地．

(1)、用含x的式子分别表示这块空地的总面积m² ，绿地的面积m²（结果保留π）．

(2)、若x＝2米时，试问小明的设计方案是否合乎要求？请说明理由（其中π取3）．

查看试题解析
20. 某市出租车的计价标准为：行驶路程不超过3千米收费10元，超过3千米的部分按每千米2.4元收费．

(1)、若某人乘坐了x（x＞3）千米，则他应支付车费元．（用含有x的代数式表示）；

(2)、一出租车公司坐落于东西向的大道边，驾驶员王师傅从公司出发，在此大道上连续接送4批客人，行驶路程记录如下（规定向东为正，向西为负，单位：千米）
第1批
第2批
第3批
第4批
+1.6
﹣9
+2.9
﹣7
①送完第4批客人后，王师傅在公司的边（填“东”或“西”），距离公司千米的位置；
②在整个过程中，王师傅共收到车费元；
③若王师傅的车平均每千米耗油0.1升，则送完第4批客人后，王师傅用了多少升油？

查看试题解析
21. 探究规律，完成相关题目．
定义“^$*$”运算：
（+2）^$*$（+4）＝+（2²+4²）；（﹣4）^$*$（﹣7）＝+[（﹣4）²+（﹣7）²]；
（﹣2）^$*$（+4）＝﹣[（﹣2）²+（+4）²]；（+5）^$*$（﹣7）＝﹣[（+5）²+（﹣7）²]；
0^$*$（﹣5）＝（﹣5）^$*$0＝（﹣5）²；（+3）^$*$0＝0^$*$（+3）＝（+3）² ．
0^$*$0＝0²+0²＝0

(1)、归纳^$*$运算的法则：
两数进行^$*$运算时，．（文字语言或符号语言均可）特别地，0和任何数进行^$*$运算，或任何数和0进行^$*$运算，．

(2)、计算：（+1）^$*$[0^$*$（﹣2）]＝．

(3)、是否存在有理数m ， n ，使得（m﹣1）^$*$（n+2）＝0，若存在，求出m ， n的值，若不存在，说明理由．

查看试题解析
22. 结合数轴与绝对值的知识回答下列问题：

(1)、数轴上表示4和1的两点之间的距离是；表示﹣3和2两点之间的距离是；一般地，数轴上表示数m和数n的两点之间的距离等于|m﹣n|．如果表示数a和﹣2的两点之间的距离是3，那么a＝；

(2)、若数轴上表示数a的点位于﹣4与2之间，求|a+4|+|a﹣2|的值；

(3)、代数式|a+5|+|a﹣1|+|a﹣4|+|a|的最小值是．

查看试题解析

第1批	第2批	第3批	第4批
+1.6	﹣9	+2.9	﹣7