广东省深圳市南山区2023-2024学年九年级上学期数学期中试卷

试卷更新日期：2023-11-22 类型：期中考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列几何体中，左视图是圆的是（）

A、 B、 C、 D、

查看试题解析
2. 人类的性别是由一对性染色体（X，Y）决定，当染色体为XX时，是女性；当染色体为XY时，是男性．如图为一对夫妻的性染色体遗传图谱，如果这位女士怀上了一个小孩，该小孩为女孩的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
3. 如果关于x的一元二次方程ax²+2x﹣1＝0有两个不相等的实数根，则a的取值范围是（）

A、a＞﹣1 B、a≥﹣1 C、a≥﹣1且a≠0 D、a＞﹣1且a≠0

查看试题解析
4. 如图，四边形 $A B C D$ 是菱形，顶点A， $C$ 的坐标分别是 $(0 ， 2)$ ， $(8 ， 2)$ ，点 $D$ 在 $x$ 轴的正半轴上，则顶点 $B$ 的坐标是（）

A、 $(4 ， 4)$ B、 $(5 ， 4)$ C、 $(2 ， 4)$ D、 $(4 ， 2)$

查看试题解析
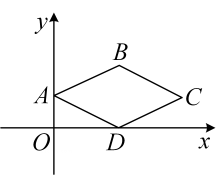5. 若 $\frac{a}{b}$ ＝ $\frac{c}{d}$ ＝ $\frac{e}{f}$ ＝ $\frac{1}{3}$ 且b﹣3d+2f≠0，则 $\frac{a - 3 c + 2 e}{b - 3 d + 2 f}$ 的值为（）

A、 $\frac{5}{6}$ B、 $\frac{1}{2}$ C、 $\frac{1}{6}$ D、 $\frac{1}{3}$

查看试题解析
6. 如图，李老师用自制的直角三角形纸板去测量灯塔的高度，他调整自己的位置，设法使斜边DF保持水平，边DE与点B在同一直线上．已知直角三角纸板中DE＝18cm ， EF＝12cm ，测得眼睛D离地面的高度为1.8m ，他与灯塔的水平距离CD为114m ，则灯塔的高度AB是（）

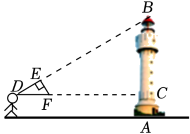A、74.2m B、77.8m C、79.6m D、79.8m

查看试题解析
7. 如图，在正方形ABCD中，AB＝3，点E ， F分别在边AB ， CD上，∠EFD＝60°，若将四边形EBCF沿EF折叠，点B'恰好落在AD边上，则BE的长度为（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析
8. 若a、b是关于x的一元二次方程x²﹣6x+n+1=0的两根，且等腰三角形三边长分别为a、b、4，则n的值为（）

A、8 B、7 C、8或7 D、9或8

查看试题解析
9. 下列命题是真命题的是（）

A、四边相等的四边形是正方形 B、物体在任何光线照射下影子的方向都是相同的 C、如果2a＝3b ，则 $\frac{a}{b} = \frac{2}{3}$ D、有一个角为120°的两个等腰三角形相似

查看试题解析
10. 如图，点P是边长为 $\sqrt{2}$ 的正方形ABCD的对角线BD上的动点，过点P分别作PE⊥BC于点E，PF⊥DC于点F，连接AP并延长，交射线BC于点H，交射线DC于点M，连接EF交AH于点G，当点P在BD上运动时（不包括B、D两点），以下结论中：①MF=MC；②AH⊥EF；③AP²=PM•PH；④EF的最小值是 $\frac{\sqrt{2}}{2}$ ．其中正确结论是（）

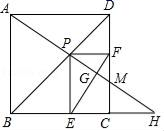A、①③ B、②③ C、②③④ D、②④

查看试题解析

二、填空题（每题3分，共15分）

11. 若 $\frac{3}{a} = \frac{2}{b}$ ，则 $\frac{a - b}{b} =$ ．

查看试题解析
12. 如图，已知AB∥CD∥EF ， AD：AF＝3：5，BC＝6，则CE的长为．

查看试题解析
13. 如图，在某校的2023年新年晚会中，舞台AB的长为20米，主持人站在点C处自然得体，已知点C是线段AB上靠近点B的黄金分割点，则此时主持人与点A的距离为米．

查看试题解析
14. 对于实数m ， n ，先定义一种运算“⊗”如下：m⊗n＝ ${\begin{cases} m^{2} + m + n ，当 m \geq n 时， \\ n^{2} + m + n ，当 m < n 时 \end{cases}$ ，若x⊗（﹣2）＝10，则实数x的值为．

查看试题解析
15. 如图，在矩形ABCD中，点E在AD上，若∠BEC＝45°且AE＝4，ED＝2，则AB的长为．

查看试题解析

三、解答题（共55分）

16. 解下列方程：

(1)、x²+2x﹣1＝0；

(2)、（x﹣2）（x﹣3）＝12．

查看试题解析
17. 为全面增强中学生的体质健康，七中育才学校开展“阳光体育活动”，开设了足球、篮球、乒乓球、羽毛球、排球等球类活动．为了解学生对这五项活动的喜爱情况，随机调查了一些学生（每名学生必选且只能选择这五项活动中的一种），根据以下统计图提供的信息，请解答下列问题：

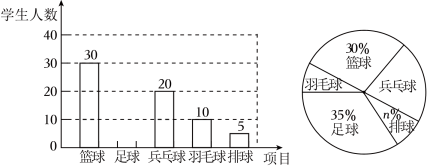(1)、本次被调查的学生有名；

(2)、扇形统计图中“排球”对应的扇形的圆心角度数是；

(3)、学校准备推荐甲、乙、丙、丁四名同学中的2名参加全市中学生排球比赛，请用列表法或树状图法分析甲和乙同学同时被选中的概率．

查看试题解析
18. 如图，在平面直角坐标系中，点A、点B的坐标分别为（1，3），（3，2）．

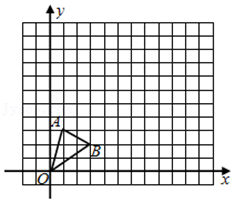(1)、画出△OAB绕点B顺时针旋转90°后的△O′A′B；

(2)、以点B为位似中心，相似比为2：1，在x轴的上方画出△O′A′B放大后的
△O″A″B；

(3)、点M是OA的中点，在（1）和（2）的条件下，M的对应点M′的坐标为．

查看试题解析
19. 如图，已知△ABC中，D是BC边上一点，过点D分别作DE∥AC交AB于点E ，作DF∥AB交AC于点F ，连接AD ．

(1)、下列条件：
①D是BC边的中点；②AD是△ABC的角平分线；③点E与点F关于直线AD对称．
请从中选择一个能证明四边形AEDF是菱形的条件，并写出证明过程；

(2)、若四边形AEDF是菱形，且AE＝4，CF＝2，求BE的长．

查看试题解析
20. “双十一”期间，某网店直接从工厂购进A ， B两款保温杯，进货价和销售价如表：（注：利润＝销售价﹣进货价）

A款保温杯
B款保温杯
进货价（元/个）
35
28
销售价（元/个）
50
40

(1)、若该网店用1540元购进A ， B两款保温杯共50个，求两款保温杯分别购进的个数．

(2)、“双十一”后，该网店打算把B款保温杯降价销售，如果按照原价销售，平均每天可售出4个，经调查发现，每降价1元，平均每天可多售出2个，则将B款保温杯的销售价定为每个多少元时，才能使B款保温杯平均每天的销售利润为96元？

查看试题解析
21. 定义：在平行四边形中，若有一条对角线长是一边长的两倍，则称这个平行四边形叫做和谐四边形，其中这条对角线叫做和谐对角线，这条边叫做和谐边．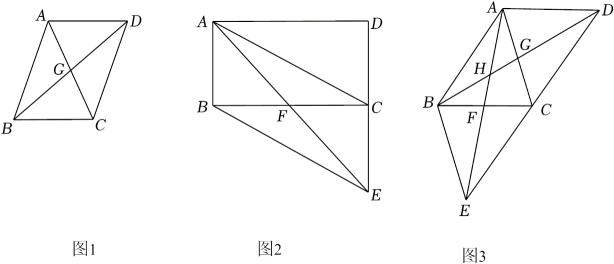

(1)、【概念理解】如图1，四边形ABCD是和谐四边形，对角线AC与BD交于点G，BD是和谐对角线，AD是和谐边．①△BCG是三角形．②若AD＝4，则BD＝；

(2)、【问题探究】如图2，四边形ABCD是矩形，过点B作BE∥AC交DC的延长线于点E，连接AE交BC于点F，AD＝4，AB＝k，是否存在实数k，使得四边形ABEC是和谐四边形，若存在，求出k的值，若不存在，请说明理由；

(3)、【应用拓展】如图3，四边形ABCD与四边形ABEC都是和谐四边形，其中BD与AE分别是和谐对角线，AD与AC分别是和谐边，AB＝4，AD＝k，请求出k的值．

查看试题解析
22.

(1)、【探究发现】
如图1，正方形ABCD的对角线交于点O ， E是AD边上一点，作OF⊥OE交AB于点F ．学习小队发现，不论点E在AD边上运动过程中，△AOE与△BOF恒全等．请你证明这个结论；

(2)、【类比迁移】
如图2，矩形ABCD的对角线交于点O ， ∠ABD＝30°，E是BA延长线上一点，将OE绕点O逆时针旋转60°得到OF ，点F恰好落在DA的延长线上，求 $\frac{A E}{A F}$ 的值；

(3)、【拓展提升】
如图3，等腰△ABC中，AB＝AC ， ∠BAC＝120°，BC＝12，点E是BC边上一点，以BE为边在BC的上方作等边△BEF ，连接CF ，取CF的中点M ，连接AM ，当AM＝ $\sqrt{7}$ 时，直接写出BE的长．

查看试题解析

	A款保温杯	B款保温杯
进货价（元/个）	35	28
销售价（元/个）	50	40