浙江省湖州市吴兴区六校联合2023-2024学年九年级第一学期数学期中试卷

试卷更新日期：2023-11-22 类型：期中考试

进入出卷网下载

一、选择题：(本大题共10小题，共30分。）

1. 下列选项中的事件，属于随机事件的是（）

A、在一个只装有黑球的袋子里，摸出白球 B、两个负数相加，和为负 C、打开电视机，正在播湖州新闻 D、在一个只装有黑球的袋子里，摸出黑球

查看试题解析
2. 抛物线 $y = x^{2} - 1$ 与y轴的交点坐标是（）

A、（0，1） B、（0，-1） C、（1，0） D、（-1，0）

查看试题解析
3. 对于函数 $y = - 2 {(x + 2)}_{}^{2} + 5$ ，下列结论错误的是（）

A、图象顶点是（－2，5） B、图象开口向下 C、图象关于直线x=－2对称 D、函数最小值为5

查看试题解析
4. 如图，一块直角三角板的30°角的顶点P落在⊙O上，两边分别交⊙O于A，B两点，连结AO，BO，则∠AOB的度数是（）

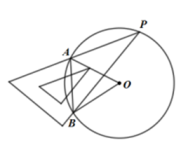A、30° B、60° C、80° D、90°

查看试题解析
5. 在一个不透明的布袋中装有若干个只有颜色不同的小球，如果袋中有红球5个，黄球4个，其余为白球，从袋子中随机摸出一个球，“摸出黄球”的概率为 $\frac{1}{3}$ ，则袋子中白球的个数为（）

A、12 B、5 C、4 D、3

查看试题解析
6. 将二次函数 $y = - 2 x^{2}$ 的图象向右平移3个单位，再向上平移 $\frac{1}{2}$ 个单位，那么所得的二次函数的解析式为（）

A、 $y = - 2 {(x - 3)}_{}^{2} - \frac{1}{2}$ B、 $y = - 2 {(x - 3)}_{}^{2} + \frac{1}{2}$ C、 $y = - 2 {(x + 3)}_{}^{2} - \frac{1}{2}$ D、 $y = - 2 {(x + 3)}_{}^{2} + \frac{1}{2}$

查看试题解析

7. 某射击运动员在同一条件下的射击成绩记录如下：

射击次数	20	80	100	200	400	1000
“射中九环以上”的次数	18	68	82	168	327	823
“射中九环以上”的频率（结果保留两位小数）	0.90	0.85	0.82	0.84	0.82	0.82

根据频率的稳定性，估计这名运动员射击一次时“射中九环以上”的概率约是（）

A、0.90 B、0.82 C、0.85 D、0.84

查看试题解析

8. 下列命题中：①任意三点确定一个圆；②同弧或等弧所对的圆心角相等；③平分弦的直径垂直于弦；④半圆所对的弦是直径.真命题的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
9. 已知已知二次函数y＝ax²+2ax+3（a>0），点P₁（﹣3，y₁），P₂（﹣1，y₂），P₃（3，y₃）是该函数图象上的3个点，则y₁ ， y₂ ， y₃的大小关系为（）．

A、Y₂＜y₃＜y₁ B、y₂＜y₁＜y₃ C、y₃＜y₁＜y₂ D、y₁＜y₃＜y₂

查看试题解析
10. 在平面直角坐标系中，对于点P（x，y）和Q（x，y′），给出如下定义：若y′＝ ${\begin{matrix} y + 1 (x \geq 0) \\ - y (x < 0) \end{matrix}$ ，则称点Q为点P的“亲密点”．例如：点（1，2）的“亲密点”为点（1，3），点（﹣1，3）的“亲密点”为点（﹣1，﹣3）．若点P在函数y＝x²﹣2x﹣3的图象上，则其“亲密点”Q的纵坐标y′关于x的函数图象大致正确的是（）

A、 B、 C、 D、

查看试题解析

二、填空题（本大题共6小题，共24分。）

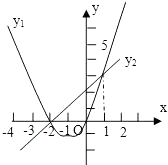
11. 已知⊙O的半径长为10cm，若点P在⊙O外，则线段OP的长度为cm．（写出一个正确的值即可）

查看试题解析
12. 对一批防PM2.5口罩进行抽检，经统计合格口罩的概率是0.9，若这批口罩共有2000只，则其中合格的大约有只．

查看试题解析
13. 如图是二次函数y₁=ax²+bx+c和一次函数y₂=mx+n的图象，观察图象写出y₂≥y₁时，x的取值范围．

查看试题解析
14. 如图是一个可以自由转动的两色转盘，其中白色扇形和红色扇形的圆心角分别为 $120 °$ 和 $240 °$ .若让转盘自由转动一次，则指针落在白色区域的概率是.若让转盘自由转动两次，则指针一次落在白色区域，另一次落在红色区域的概率是.

查看试题解析
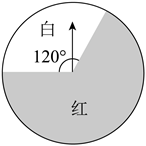15. 二次函数y=ax²+bx+c的图象如图所示，对称轴是直线x=1.下列结论：①abc﹤0；②3a+c﹥0；③(a+c)²-b²﹤0；④a+b≤m(am+b)(m为实数).其中正确的结论有.

查看试题解析
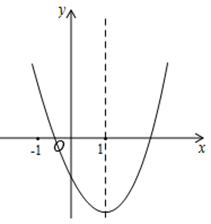16. 在平面直角坐标系内，已知点A（−1，0），点B（1，1），连结AB，若抛物线y＝ax²−x＋1（a≠0）与线段AB有两个不同的交点，则a的取值范围是.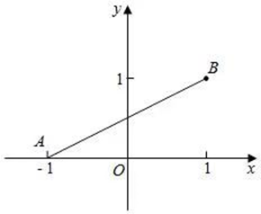

查看试题解析

三、解答题（本大题共8小题，其中17、18、19各6分，20、21各8分，22、23各10分，24题12分，共66分）

17. 已知二次函数的图象经过（0，0），且它的顶点坐标是（1，－2）.

(1)、求这个二次函数的关系式；

(2)、判断点P（3，5）是否在这条抛物线的图像上.

查看试题解析
18. 在一个不透明的口袋中装有4个依次写有数字1，2，3，4的小球，它们除数字外都相同，每次摸球前都将小球摇匀.

(1)、从中随机摸出一个小球，小球上写的数字不大于3的概率是；

(2)、若从中随机摸出一球不放回，再随机摸出一球，请用画树状图或列表的方法，求两次摸出小球上的数字和恰好是偶数的概率.

查看试题解析
19. 如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C.

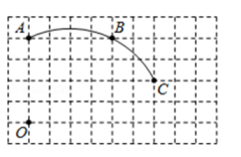(1)、请完成如下操作：
①以点 $O$ 为原点、竖直和水平方向为轴、网格边长为单位长，建立平面直角坐标系；
②根据图形提供的信息，标出该圆弧所在圆的圆心 $D$ ，并连结 $A D$ 、 $C D$

(2)、请在（1）的基础上，完成下列填空：
①写出点的坐标： $C$ 、 $D$ ．
②⊙D的半径 $=$ （结果保留根号）

查看试题解析
20. 已知抛物线y=ax²+x+1（ $a \neq 0$ ）

(1)、若抛物线的图象与x轴只有一个交点，求a的值；

(2)、若抛物线的顶点始终在x轴上方，求a的取值范围．

查看试题解析
21. 如图，AB是⊙O的直径，弦CD⊥AB于点E，连接AD，BD，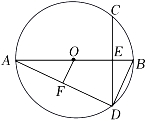

(1)、求证：∠ADC＝∠ABD．

(2)、作OF⊥AD于点F，若⊙O的半径为5，OE＝3，求OF的长．

查看试题解析
22. “互联网+”时代，网上购物备受消费者青睐.某网店专售一款休闲裤，其成本为每条40元，当售价为每条80元时，每月可销售100条.为了吸引更多顾客，该网店采取降价措施.据市场调查反映：销售单价每降1元，则每月可多销售5条.设每条裤子的售价为x元（x为正整数），每月的销售量为y条.

(1)、直接写出y与x的函数关系式；

(2)、设该网店每月获得的利润为w元，当销售单价降低多少元时，每月获得的利润最大，最大利润是多少？

(3)、该网店店主热心公益事业，决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元，且让消费者得到最大的实惠，该如何确定休闲裤的销售单价？

查看试题解析
23. 在平面直角坐标系中，抛物线y＝−x²−4x＋c与x轴交于点A、B（点A在点B的左侧），与y轴交于点C，且点A的坐标为（−5，0）．

(1)、求点C的坐标和直线AC的解析式；

(2)、如图，若点M是抛物线上一点，点N是抛物线对称轴上一点，是否存在点M使以A，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．

查看试题解析
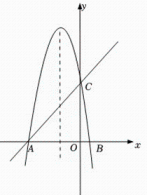24. 如图所示，抛物线 $y = a x^{2} + b x + c (a < 0)$ 与双曲线 $y = \frac{k}{x}$ 相交于点A、B，且抛物线经过坐标原点，点A的坐标为（-2，2），点B在第四象限内，过点B作直线BC∥x轴，C为直线BC与抛物线的另一交点，已知直线BC与x轴之间的距离是点B到y轴距离的4倍，记抛物线的顶点为E。

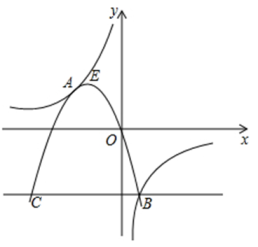(1)、求双曲线和抛物线的函数关系式；

(2)、计算△ABC与△ABE的面积；

(3)、在抛物线上是否存在点D，使∆ABD的面积等于∆ABE的面积的8倍？若存在，请求出点D的坐标；若不存在，请说明理由。

查看试题解析

浙江省湖州市吴兴区六校联合2023-2024学年九年级第一学期数学期中试卷

一、选择题：(本大题共10小题，共30分。）

二、 填空题（本大题共6小题，共24分。）

三、解答题（本大题共8小题，其中17、18、19各6分，20、21各8分，22、23各10分，24题12分，共66分）

二、填空题（本大题共6小题，共24分。）