浙江省湖州市吴兴区六校联合2023-2024学年七年级第一学期数学期中试卷

试卷更新日期：2023-11-22 类型：期中考试

进入出卷网下载

一、选择题：（本大题共10小题，共30分）

1. 2的绝对值是（）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、2 D、﹣2

查看试题解析
2. 下列实数中，无理数是（）

A、 $\frac{1}{3}$ B、0.2 C、0 D、 $\sqrt{2}$

查看试题解析
3. 4的算术平方根是（）

A、 4 B、±4 C、2 D、±2

查看试题解析
4. 在0，2， $- \frac{1}{3}$ ， −2四个数中，最小的数是（）

A、0 B、2 C、 $- \frac{1}{3}$ D、−2

查看试题解析
5. 表示“ $m$ 的5倍与 $n$ 的平方的差”的代数式是（）

A、 ${(5 m)}^{2} - n^{2}$ B、 $5 m - n^{2}$ C、 ${(5 m - n)}^{2}$ D、 $5 m^{2} - n^{2}$

查看试题解析
6. 下列叙述正确的是（）

A、m的系数是0，次数为1 B、单项式xy²z³的系数为1，次数是6 C、当m=2时，代数式5﹣2m²等于1 D、多项式2a²﹣3a﹣5次数为2，常数项为5

查看试题解析
7. 下列各式可以写成 $a - b + c$ 的是（）

A、 $a - (+ b) - (+ c)$ B、 $a - (+ b) - (- c)$ C、 $a + (- b) + (- c)$ D、 $a + (- b) - (+ c)$

查看试题解析
8. 如图所示，数轴上点A、B对应的有理数分别为a、b ，下列说法正确的是（）

A、ab＞0 B、|a|＜|b| C、a+b＞0 D、a﹣b＜0

查看试题解析
9. 近似数65.07万精确到（）

A、百位 B、百分位 C、万位 D、个位

查看试题解析
10. 历史上，数学家欧拉最先把关于 $x$ 的多项式用记号 $f (x)$ 来表示，把 $x$ 等于某数 $a$ 的多项式的值用 $f (a)$ 来表示．例如x=-3时，多项式 $f (x) = - 3 x^{2} + x$ 的值记为 $f (- 3)$ ，那么 $f (- 3)$ 的值等于（）

A、-30 B、-27 C、24 D、30

查看试题解析

二、填空题（本大题共6小题,共24分）

11. 如果向东行驶3米，记作+3米，那么向西行驶5米，记作米．

查看试题解析
12. 2023年2月10日，神舟十五号航天员乘组圆满完成了他们的首次出舱任务．飞船的时速为每小时28亿千米，2800000000000米用科学记数法表示应为米．

查看试题解析
13. 一个立方体的体积是125cm³ ，则它的棱长是cm.

查看试题解析
14. 若 ${(a + 2)}_{}^{2} + \sqrt{b - 1} = 0$ ，则 $a + b$ 的值为．

查看试题解析
15. 若 $| x | = 3 ， y_{}^{2} = 16 ，且 x y < 0 ，则 2 x + y 的值为$ .

查看试题解析
16. 根据图中的程序，当输入x为64时，输出的值是．

查看试题解析

三、解答题（本大题共8小题，其中17、18、19各6分，20、21各8分，22、23各10分，24题12分，共66分）

17. 在数轴上表示下列各数： $+ 3 ， 0 ， - 3.5 ， - \frac{1}{3}$ 并用“ $<$ ”把各数连接起来

查看试题解析
18. 计算：

(1)、 $- 25 - (- 17) + (- 10)$

(2)、 $- 1_{}^{2} - (1 - 0.25) \div 2 \frac{1}{3} \times [- 20 + {(- 2)}_{}^{3}]$

查看试题解析
19. 将下列各数填在相应的大括号里：
$\frac{π}{2}$ ， $- | - 3 |$ ， $0$ ， $\frac{22}{7}$ ， $－ 3 . \dot{1}$ ， $1.1010010001$ …（两个1之间依次多 $1$ 个 $0$ ）
整数{}；
分数{}；
无理数{}．

查看试题解析
20. 已知x ， y为有理数，如果规定一种运算“*”，即x*y＝xy+1，试根据这种运算完成下列各题．

(1)、求2*4；

(2)、求（2*5）*（﹣3）；

(3)、任意选择两个有理数x ， y ，分别计算x*y和y*x ，并比较两个运算结果，你有何发现？

查看试题解析
21. 某果农把自家果园的柑橘包装后放到了网上销售．原计划每天卖10箱，但由于种种原因，实际每天的销售量与计划量相比有出入，下表是某个星期的销售情况（超额记为正，不足记为负，单位：箱）．
星期
一
二
三
四
五
六
日
与计划量的差值
+4
﹣3
﹣5
+7
﹣8
+21
﹣6

(1)、根据记录的数据可知前五天共卖出多少箱？

(2)、本周实际销售总量达到了计划数量没有？

(3)、若每箱柑橘售价为80元，同时需要支出运费7元/箱，那么该果农本周总共收入多少元？

查看试题解析
22. 下面是小李同学探索 $\sqrt{107}$ 的近似数的过程：
$∵$ 面积为107的正方形边长是 $\sqrt{107}$ ，且 $10 < \sqrt{107} < 11$ ，
$∴$ 设 $\sqrt{107} = 10 + x$ ，其中 $0 < x < 1$ ，画出如图示意图，
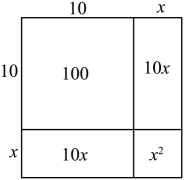
因为图中 $S_{正方形}^{} ＝ 100 + 2 \times 10 x + x_{}^{2}$ ， $S_{正方形} = 107$ ，
所以 $100 + 2 \times 10 x + x_{}^{2} = 107$
当 $x^{2}$ 较小时，省略 $x^{2}$ ，得 $20 x + 100 \approx 107$ ，得到 $x \approx 0.35$ ，即 $\sqrt{107} \approx 10.35$ ．

(1)、 $\sqrt{76}$ 的整数部分是；

(2)、仿照上述方法，探究 $\sqrt{76}$ 的近似值．（画出示意图，标明数据，并写出求解过程）

查看试题解析
23. 观察下列等式：
第1个等式： $a_{1} = \frac{1}{1 \times 3} = \frac{1}{2} \times (1 - \frac{1}{3})$ ；第2个等式： $a_{2} = \frac{1}{3 \times 5} = \frac{1}{2} \times (\frac{1}{3} - \frac{1}{5})$ ；
第3个等式： $a_{3} = \frac{1}{5 \times 7} = \frac{1}{2} \times (\frac{1}{5} - \frac{1}{7})$ ；第4个等式： $a_{4} = \frac{1}{7 \times 9} = \frac{1}{2} \times (\frac{1}{7} - \frac{1}{9})$ ．
请解答下列问题：

(1)、按着以上的规律，可以写出第5个等式为： $a_{5} =$ ；

(2)、用含有n（n为正整数）代数式表示第n个等式： $a_{n} =$ ；

(3)、直接写出当 $a_{n} = \frac{1}{143}$ 时，n的值为；

(4)、求 $a_{1} + a_{2} + a_{3} + a_{4} + \dots + a_{50}$ 的值．

查看试题解析
24. 结合数轴与绝对值的知识回答下列问题：

(1)、数轴上表示4和1的两点之间的距离是；表示-3和2的两点之间的距离是；一般地，数轴上表示数 $m$ 和数 $n$ 的两点之间的距离等于 $|m - n| .$ 如果表示 $数 a$ 和-2的两点之间的距离是3，那么 $a =$ .

(2)、若数轴上表示数 $a$ 的点位于 $- 4$ 和 $2$ 之间，求 $|a + 4| + |a - 2|$ 的值.

(3)、满足 $|a + 1| + |a + 4| > 3$ 的 $a$ 的取值范围是.

(4)、已知数轴上两点A、B，其中点A表示的数为-2，点B表示的数为2，若在数轴上存在一点C，使得AC+BC=n（把点A到点C的距离记为AC，点B到点C的距离记为BC），则称点C为点A、B的“n节点”.例如：若点C表示的数为0，有AC+BC＝2+2＝4，则称点C为点A、B的“4节点”.
若点 $E$ 在数轴上（不与点A、B重合），满足 $B E = 3 A E$ ，且此时点E为点A、B的“n节点”，求n的值.

查看试题解析

星期	一	二	三	四	五	六	日
与计划量的差值	+4	﹣3	﹣5	+7	﹣8	+21	﹣6