浙江省杭州市主城区八校2023-2024学年九年级上学期数学期中联考试卷
试卷更新日期:2023-11-22 类型:期中考试
一、选择题:(共10小题,3×10=30分)
-
1. 下列事件中是不可能事件的是( )A、守株待兔 B、瓮中捉鳖 C、水中捞月 D、百步穿杨2. 已知点A在直径为8cm的⊙O内,则OA的长可能是( )A、8cm B、6cm C、4cm D、2cm3. 二次函数的图象平移后经过点 , 则下列平移方法正确的是( )A、向右平移2个单位,向上平移1个单位 B、向右平移1个单位,向下平移1个单位 C、向左平移1个单位,向上平移2个单位 D、向左平移2个单位,向下平移2个单位4. 从-1,2,3,6这四个数中任取不同的两数,分别记为m,n,那么点(m,n)在函数图象上的概率是( )A、 B、 C、 D、5. 已知圆中两条平行的弦之间距离为1,其中一弦长为8,若半径为5,则另一弦长为( )A、6或 B、6或7 C、6或 D、7或96. 下列命题正确的是( )A、相等的弦所对的弧相等 B、平分弦的直径平分弦所对的两条弧 C、过三点能作一个圆 D、在同心圆中,同一圆心角所对的两条弧的度数相等7. 已知二次函数 , 对于其图象和性质,下列说法错误的是( )A、图象开口向下 B、图象经过原点 C、当时,y随x的增大而减小,则 D、函数一定存在最大值8. 如图,将半径为6的⊙O沿AB折叠,使得折痕AB垂直半径OC,当恰好经过CO的三等分点D(靠近端点O)时,折痕AB长为( )
 A、 B、 C、 D、9. 如图,已知 , AB=4,AC=6,点P在内,将绕着点A逆时针方向旋转60°得到.则AE+PB+PC的最小值为( )
A、 B、 C、 D、9. 如图,已知 , AB=4,AC=6,点P在内,将绕着点A逆时针方向旋转60°得到.则AE+PB+PC的最小值为( ) A、 B、 C、 D、10. 已知二次函数满足以下三个条件:① , ② , ③ , 则它的图象可能是( )A、
A、 B、 C、 D、10. 已知二次函数满足以下三个条件:① , ② , ③ , 则它的图象可能是( )A、 B、
B、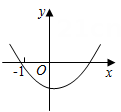 C、
C、 D、
D、
二、填空题:(共6小题,4×6=24分)
-
11. 掷一枚质地均匀的硬币,前9次都是反面朝上,则掷第10次时反面朝上的概率是 .12. 已知二次函数 , 其顶点坐标为.13. 如图,在⊙O中,BA=BC,的度数为80°,则∠BCO=.
 14. 如图,已知一次函数 , 二次函数 , 两函数图象交于点(3,m),(n,-6),当时,x的取值范围为.
14. 如图,已知一次函数 , 二次函数 , 两函数图象交于点(3,m),(n,-6),当时,x的取值范围为.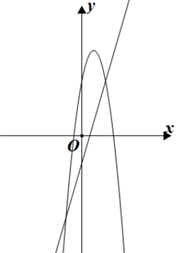 15. 如图,一条形状一定的抛物线与x轴相交于A、B两点(点A在点B的左侧),其顶点P在线段MN上移动.若点M、N的坐标分别为(-1,-2)、(1,-2),点A的横坐标的最小值为-3,则点B横坐标的最大值为.
15. 如图,一条形状一定的抛物线与x轴相交于A、B两点(点A在点B的左侧),其顶点P在线段MN上移动.若点M、N的坐标分别为(-1,-2)、(1,-2),点A的横坐标的最小值为-3,则点B横坐标的最大值为. 16. 如图,抛物线与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连结OQ.则线段OQ的最大值是.
16. 如图,抛物线与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连结OQ.则线段OQ的最大值是.
三、解答题:(共8小题,6+6+6+8+8+10+10+12=66分)
-
17. 已知二次函数的图象经过点(1,0),(0,).(1)、求该二次函数的表达式;(2)、求出二次函数的图象与x轴的另一个交点坐标.18. 如图,每个小方格都是边长为1个单位长度,ABC在坐标系中的位置如图所示.

⑴作出ABC绕原点O逆时针方向旋转90°后的;
⑵作出ABC的点B绕原点O逆时针方向旋转90°后经过的路线.
⑶请直接写出ABC的外接圆圆心坐标为 ▲ .
19. 在一个不透明的口袋中装有若干个相同的红球,为估计袋中红球的数量,九(1)班学生分组进行摸球试验:每组先将10个与红球形状大小完全相同的白球装入袋中,搅匀后随机摸出一个球并记下颜色,再把它放回袋中,不断重复.以下是这次活动统计汇总各小组数据后获得的全班数据统计表:摸球的次数s
150
300
600
900
1200
1500
摸到白球的频数n
63
a
247
365
484
606
摸到白球的频率
0.420
0.410
0.412
0.406
0.403
b
(1)、按表格数据格式,表中的a=;b=;(2)、请估计:当次数s很大时,摸到白球的频率将会接近(精确到0.1);(3)、请推算:摸到红球的概率是(精确到0.1);(4)、试估算:这一个不透明的口袋中红球有个.20. 已知:如图,在⊙O中,= , AB与CD相交于点M.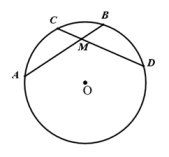
求证:
(1)、AB=CD;(2)、AM=DM.21. 已知一座圆弧形拱桥,圆心为点O,桥下水面宽度AB为18m,过O作OC⊥AB于点D,CD=3m.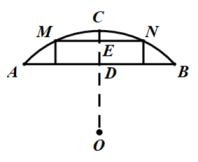 (1)、 求该圆弧形拱桥的半径;(2)、现有一艘宽6m,船舱顶部高出水面2m的货船要经过这座拱桥(船舱截面为长方形),请问,该货船能顺利通过吗?22. 已知二次函数的图象与x轴有交点.(1)、求k的取值范围;(2)、若函数图象与x轴有两个交点,且满足.
(1)、 求该圆弧形拱桥的半径;(2)、现有一艘宽6m,船舱顶部高出水面2m的货船要经过这座拱桥(船舱截面为长方形),请问,该货船能顺利通过吗?22. 已知二次函数的图象与x轴有交点.(1)、求k的取值范围;(2)、若函数图象与x轴有两个交点,且满足.①求k的值;
②当时,求y的取值范围.
23. 如图,已知⊙O的半径长为1,AB、AC是⊙O的两条弦,且AB=AC,BO的延长线交AC于点D,连结OA,OC.
 (1)、求证:△OAB≌△OAC.(2)、当BA=BD时,求的度数.(3)、当△OCD是直角三角形时,求B、C两点之间的距离.24. 如图,已知排球场的长度OD为18米,位于球场中线处的球网AB的高度2.43米,一队员站在点O处发球,排球从点O的正上方1.8米的C点向正前方飞去,排球的飞行路线是抛物线的一部分,当排球运行至离点O的水平距离OE为7米时,到达最高点G,以O为原点建立如图所示的平面直角坐标系.
(1)、求证:△OAB≌△OAC.(2)、当BA=BD时,求的度数.(3)、当△OCD是直角三角形时,求B、C两点之间的距离.24. 如图,已知排球场的长度OD为18米,位于球场中线处的球网AB的高度2.43米,一队员站在点O处发球,排球从点O的正上方1.8米的C点向正前方飞去,排球的飞行路线是抛物线的一部分,当排球运行至离点O的水平距离OE为7米时,到达最高点G,以O为原点建立如图所示的平面直角坐标系. (1)、若排球运行的最大高度为3.2米,求排球飞行的高度y(单位:米)与水平距离x(单位:米)之间的函数关系式(不要求写自变量x的取值范围);(2)、在(1)的条件下,这次所发的球能够过网吗?如果能够过网,是否会出界?请说明理由;(3)、若队员发球既要过球网,排球又不会出界(排球压线属于没出界),求二次函数中二次项系数的范围.
(1)、若排球运行的最大高度为3.2米,求排球飞行的高度y(单位:米)与水平距离x(单位:米)之间的函数关系式(不要求写自变量x的取值范围);(2)、在(1)的条件下,这次所发的球能够过网吗?如果能够过网,是否会出界?请说明理由;(3)、若队员发球既要过球网,排球又不会出界(排球压线属于没出界),求二次函数中二次项系数的范围.