浙江省杭州市主城区八校2023-2024学年八年级上学期数学期中联考试卷
试卷更新日期:2023-11-22 类型:期中考试
一、选择题(共10小题,每小题3分,共30分)
-
1. 下列图形中,为轴对称的图形的是( )A、
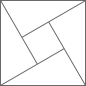 B、
B、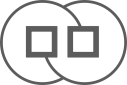 C、
C、 D、
D、 2. 已知三角形的三边长分别为4,5,x,则x不可能是( )A、3 B、5 C、7 D、93. 在△ABC中,画出边AC上的高,画法正确的是( )
2. 已知三角形的三边长分别为4,5,x,则x不可能是( )A、3 B、5 C、7 D、93. 在△ABC中,画出边AC上的高,画法正确的是( )
A、 B、
B、 C、
C、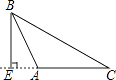 D、
D、 4. 对于命题“如果∠1=∠2=90°,那么∠1与∠2互补”,能说明这个命题的逆命题是假命题的反例是( )A、∠1=80°,∠2=110° B、∠1=10°,∠2=169° C、∠1=60°,∠2=120° D、∠1=60°,∠2=140°5. 在△ABC中,线段AP , AQ , AR分别是BC边上的高线,中线和角平分线,则( )A、AP≤AQ B、AQ≤AR C、AP>AR D、AP>AQ6. 根据下列已知条件,能画出唯一的△ABC的是( )A、AB=3,BC=4,AC=7 B、AB=4,BC=3,∠A=30° C、∠A=60°,∠B=45°,AC=4 D、∠A=∠B,AB=67. 如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC . 若DE=5,AE=8,EC= , 则BC的长度是( )
4. 对于命题“如果∠1=∠2=90°,那么∠1与∠2互补”,能说明这个命题的逆命题是假命题的反例是( )A、∠1=80°,∠2=110° B、∠1=10°,∠2=169° C、∠1=60°,∠2=120° D、∠1=60°,∠2=140°5. 在△ABC中,线段AP , AQ , AR分别是BC边上的高线,中线和角平分线,则( )A、AP≤AQ B、AQ≤AR C、AP>AR D、AP>AQ6. 根据下列已知条件,能画出唯一的△ABC的是( )A、AB=3,BC=4,AC=7 B、AB=4,BC=3,∠A=30° C、∠A=60°,∠B=45°,AC=4 D、∠A=∠B,AB=67. 如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC . 若DE=5,AE=8,EC= , 则BC的长度是( ) A、 B、8 C、 D、8. 如图,Rt△ABC中,∠A=90°,AB=3,AC=4,现将△ABC沿BD进行翻折,使点A刚好落在BC上,则CD的长为( )
A、 B、8 C、 D、8. 如图,Rt△ABC中,∠A=90°,AB=3,AC=4,现将△ABC沿BD进行翻折,使点A刚好落在BC上,则CD的长为( ) A、 B、 C、2 D、9. 如图,AB=AD , 点B关于AC的对称点E恰好落在CD上,若∠BAD=α(0°<α<180°),则∠ACB的度数为( )
A、 B、 C、2 D、9. 如图,AB=AD , 点B关于AC的对称点E恰好落在CD上,若∠BAD=α(0°<α<180°),则∠ACB的度数为( ) A、90°-α B、α C、45° D、α-45°10. 如图,BD是△ABC的角平分线,BA=BC=10,AC=12,DE∥BC , P , Q分别是BD和BC上的任意一点;连接PA , PC , PQ , AQ , 给出下列结论:①PC+PQ≥AQ;②AE+DE=BC;③PC+PQ的最小值是;④若PA平分∠BAC , 则△APD的面积为9.其中正确的是( )
A、90°-α B、α C、45° D、α-45°10. 如图,BD是△ABC的角平分线,BA=BC=10,AC=12,DE∥BC , P , Q分别是BD和BC上的任意一点;连接PA , PC , PQ , AQ , 给出下列结论:①PC+PQ≥AQ;②AE+DE=BC;③PC+PQ的最小值是;④若PA平分∠BAC , 则△APD的面积为9.其中正确的是( ) A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题(本大题共6小题,每小题4分,共24分)
-
11. 命题“如果a=b , 那么a2=b2”的逆命题是 , 逆命题是命题.(填“真”或“假”).12. 如图,∠ACD是△ABC的一个外角,若∠ACD=110°,∠B=45°,则∠A= .
 13. 若等腰三角形一个内角的度数为50°,则它的顶角的度数是 .14. 如图,∠C=90°,AD平分∠BAC交BC于D,若BC=7cm,BD=4cm,则点D到AB的距离为cm.
13. 若等腰三角形一个内角的度数为50°,则它的顶角的度数是 .14. 如图,∠C=90°,AD平分∠BAC交BC于D,若BC=7cm,BD=4cm,则点D到AB的距离为cm. 15. 如图,CD是△ABC的角平分线,AE⊥CD于E,BC=6,AC=4,△ABC的面积是9,则△AEC的面积是.
15. 如图,CD是△ABC的角平分线,AE⊥CD于E,BC=6,AC=4,△ABC的面积是9,则△AEC的面积是.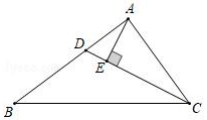 16. 如图,已知等边△ABC的边长为4,点P是边BC上一点,BP=1,则AP= , 若点Q是边AC上一点,BQ=AP , 则AQ= .
16. 如图,已知等边△ABC的边长为4,点P是边BC上一点,BP=1,则AP= , 若点Q是边AC上一点,BQ=AP , 则AQ= .
三、解答题(共8小题,66分,解答应写出文字说明或推理步骤)
-
17. 如图,正方形网格中的每个小正方形的边长都是1,每个小方格的顶点叫做格点,以格点为顶点分别按下列要求画三角形:
 (1)、在图1中画一个直角三角形,使它的三边长都是有理数;(2)、在图2中画一个直角三角形,使它的三边长都是无理数;(3)、在图3中画一个等腰三角形,使它的三边长都是无理数(和图2画的三角形不全等).18. 如图,△ABC中,∠B=30°,∠C=40°.
(1)、在图1中画一个直角三角形,使它的三边长都是有理数;(2)、在图2中画一个直角三角形,使它的三边长都是无理数;(3)、在图3中画一个等腰三角形,使它的三边长都是无理数(和图2画的三角形不全等).18. 如图,△ABC中,∠B=30°,∠C=40°. (1)、尺规作图:作AB的垂直平分线交BC于点D , 交AB于点E . (保留作图痕迹,不写作法)(2)、连结AD , 求∠DAC的度数.19. 如图,△ABC与△DCB中,AC与BD交于点E , 且∠A=∠D , AB=DC .
(1)、尺规作图:作AB的垂直平分线交BC于点D , 交AB于点E . (保留作图痕迹,不写作法)(2)、连结AD , 求∠DAC的度数.19. 如图,△ABC与△DCB中,AC与BD交于点E , 且∠A=∠D , AB=DC . (1)、求证:△ABE≌△DCE;(2)、当∠AEB=80°,求∠EBC的度数.20. 如图,CD=BE,DG⊥BC,EF⊥BC,垂足分别为G,F,且DG=EF.
(1)、求证:△ABE≌△DCE;(2)、当∠AEB=80°,求∠EBC的度数.20. 如图,CD=BE,DG⊥BC,EF⊥BC,垂足分别为G,F,且DG=EF. (1)、求证:OB=OC;(2)、若∠B=30°,判断△ADO的形状,并说明理由.21. 如图所示,在△ABC中,AB=BC , 点D是BC上一点,DE⊥AB于点E , DF⊥BC , 交AC于点F , 连接BF .
(1)、求证:OB=OC;(2)、若∠B=30°,判断△ADO的形状,并说明理由.21. 如图所示,在△ABC中,AB=BC , 点D是BC上一点,DE⊥AB于点E , DF⊥BC , 交AC于点F , 连接BF . (1)、若∠AFD=155°,求∠EDF的度数;(2)、若点F是AC的中点,判断∠ABC与∠CFD的数量关系,并说明理由.22. 已知,DA , DB , DC是从点D出发的三条线段,且DA=DB=DC .
(1)、若∠AFD=155°,求∠EDF的度数;(2)、若点F是AC的中点,判断∠ABC与∠CFD的数量关系,并说明理由.22. 已知,DA , DB , DC是从点D出发的三条线段,且DA=DB=DC . (1)、如图①,若点D在线段AB上,连接AC , BC , 试判断△ABC的形状,并说明理由.(2)、如图②,连接AC , BC , AB , 且AB与CD相交于点E , 若AC=BC , AB=16,DC=10,求CE的长.
(1)、如图①,若点D在线段AB上,连接AC , BC , 试判断△ABC的形状,并说明理由.(2)、如图②,连接AC , BC , AB , 且AB与CD相交于点E , 若AC=BC , AB=16,DC=10,求CE的长.

