浙江省杭州市主城区八校2023-2024学年七年级上学期数学期中联考试卷

试卷更新日期：2023-11-22 类型：期中考试

进入出卷网下载

一、选择题（本大题有10小题，每小题3分，共30分.请选出每小题中一个最符合题意的选项，不选、多选、错选，均不给分）

1. 在－1，2，0，－3这四个数中，最小的数是（）

A、－1 B、2 C、0 D、－3

查看试题解析
2. －2023的相反数等于（）

A、2023 B、－2023 C、－ $\frac{1}{2023}$ D、 $\frac{1}{2023}$

查看试题解析
3. 在实数 $- \sqrt{3}$ ， $- \sqrt{\frac{16}{9}}$ ， $0 . \dot{6}$ ， $\frac{22}{7}$ ， 0， $\sqrt[3]{- 6}$ ， 0.101001000100001中，无理数有（）个.

A、2 B、3 C、4 D、5

查看试题解析
4. 杭州奥体中心体育场俗称“大莲花”，为杭州亚运会主体育场馆及田径项目比赛场地，总建筑面积约216000平方米，将数216000用科学记数法表示为（）

A、0.216× $10^{6}$ B、2.16× $10^{5}$ C、21.6× $10^{4}$ D、216× $10^{3}$

查看试题解析
5. 下列运算正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 ${(- 2)}^{3} = 8$ C、 $- |- 3| = - 3$ D、 $- 2^{2}$ =4

查看试题解析
6. 用代数式表示a ， b两数的平方和是（）

A、 $a^{2} + b$ B、 $a + b^{2}$ C、 $a^{2} + b^{2}$ D、 ${(a + b)}^{2}$

查看试题解析
7. 下列无理数中，大小在3与4之间的是（）

A、 $\sqrt{5}$ B、 $\sqrt{7}$ C、 $\sqrt{13}$ D、 $\sqrt{17}$

查看试题解析
8. 如图， $a$ ， $b$ 是有理数，它们在数轴上的对应点的位置如图所示，把 $a$ ， $- a$ ， $b$ ， $- b$ 按照从大到小的顺序排列，正确的是（）

A、 $b > - a > a > - b$ B、 $b > a > - a > - b$ C、 $- a > b > a > - b$ D、 $- a > - b > a > b$

查看试题解析
9. 下列说法：①有理数与数轴上的点一一对应；②1的平方根是它本身；③立方根是它本身的数是0，1；④对于任意一个实数 $a$ ，都可以用 $\frac{1}{a}$ 表示它的倒数．⑤任何无理数都是无限不循环小数.正确的有（）个.

A、0 B、1 C、2 D、3

查看试题解析
10. 观察下列等式：7¹＝7，7²＝49，7³＝343，7⁴＝2401，7⁵＝16087，…，那么7¹+7²+7³+7⁴+7⁵…+7²⁰²³的末位数字是（）

A、1 B、3 C、7 D、9

查看试题解析

二、填空题（本大题有6小题，每小题4分，共24分）

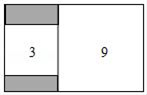
11. “a的相反数与b的倒数的差”，用代数式表示为.

查看试题解析
12. $\frac{1}{16}$ 的算术平方根是； $\sqrt{81}$ 的平方根是．

查看试题解析
13. 由四舍五入得到的近似数1.20万精确到位.由四舍五入得到的近似数37.5精确到位，它表示大于或等于，而小于的数.

查看试题解析
14. 数轴上点A表示的数是1，点B ， C分别位于点A的两侧，且到点A的距离相等.若点B表示的数是 $\sqrt{3}$ ，则点C表示的数是.

查看试题解析
15. 如图，长方形内有两个相邻的正方形，面积分别为3和9，那么阴影部分的面积为.

查看试题解析
16. 某次会议前，小明同学帮助老师摆放桌椅：
甲方式：……
乙方式：……

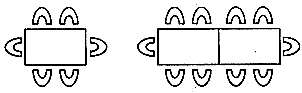(1)、按甲方式将4张桌子拼在一起共有个座位， $n$ 张桌子拼在一起共有个座位；

(2)、按乙方式将6张桌子拼在一起共有个座位， $m$ 张桌子拼在一起共有个座位.

查看试题解析

三、解答题（本大题共8个小题，共66分，解答应写出演算步骤）

17. 计算：

(1)、(-7)-(-13)

(2)、 $(- \frac{2}{5}) + (- 3 \frac{4}{7}) - 1 \frac{3}{5} - (- \frac{11}{7})$

查看试题解析
18. 计算：

(1)、 $(- 24) \times (\frac{1}{8} - \frac{1}{3} + \frac{1}{4})$

(2)、 $- 3^{2} \div (\frac{1}{3} - \frac{1}{2})$

查看试题解析
19. 计算：

(1)、 $- \sqrt{1.44} + \sqrt[3]{- 0.001}$

(2)、 $6 + 2 \times (\sqrt{5} - 3) - 2 (\sqrt{5} - 1)$

查看试题解析
20. 一只蚂蚁从某点P出发，在一条直线上来回爬行.记向右爬行的路程为正数，向左爬行的路程为负数，爬行的路程依次为（单位：厘米）：＋7，－9，－5，－4，＋13，－2.

(1)、通过计算说明蚂蚁是否回到起点.

(2)、若蚂蚁爬行的速度为0.5厘米/秒，则蚂蚁共爬行了多少时间？

查看试题解析
21. 为了加强公民的节水意识，合理利用水资源，某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.
价目表
每月用水量
单价
不超出6m³的部分
2元/m³
超出6m³ ，不超出10m³的部分
4元/m³
超出10m³的部分
8元/m³
注：水费按月结算.
若某户居民1月份用水8.3m³ ，则应收水费：2×6+4×(8.3-6)=21.2（元）

(1)、若该户居民2月份收水费16元，计算该户2月份用水量；

(2)、若该户居民3月份用水12.5m³ ，则应收水费多少元？

查看试题解析
22.

(1)、已知某正数的平方根为a+3和2a-9，求这个数是多少？

(2)、已知 $m$ ， $n$ 是实数，且 $\sqrt{2 m + 1} + | 3 n - 2 | = 0$ ，求 $m^{2} + n^{2}$ 的平方根．

查看试题解析
23. 如图1，这是一个3阶魔方，由三层完全相同的27个小立方体组成，体积为27.

(1)、求出这个魔方的棱长．

(2)、图中阴影部分是一个正方形ABCD ，求出阴影部分的面积及其边长．

(3)、在图2的4×4方格中画一个面积为10的正方形；并将数轴补充完整，然后用圆规在数轴上表示实数 $- \sqrt{10}$ .

查看试题解析
24. 已知数轴上点 $A$ 表示的数为 $- 5$ ，点 $B$ 是数轴上在点 $A$ 右侧的一点，且 $A$ 、 $B$ 两点间的距离为 $8$ 个单位长度，点 $P$ 为数轴上的一个动点，其对应的数为 $x$ ．

(1)、写出点 $B$ 所表示的数为．

(2)、①若点 $P$ 到点 $A$ ，点 $B$ 的距离相等，则点 $P$ 所表示的数为 ▲ ．
②数轴上是否存在点 $P$ ，使点 $P$ 到点 $A$ ，点 $B$ 的距离之和为 $10$ ，若存在，求出 $x$ 的值，若不存在，说明理由．

(3)、若点 $P$ 从 $A$ 点出发，以每秒 $3$ 个单位长度的速度向左作匀速运动，点 $Q$ 从 $B$ 出发，以每秒 $5$ 个单位长度的速度向左作匀速运动， $P$ ， $Q$ 同时运动：
$①$ 当点 $P$ 运动多少秒时，点 $P$ 和点 $Q$ 重合？
$②$ 当点 $P$ 运动多少秒时， $P$ ， $Q$ 之间的距离为 $3$ 个单位长度？

查看试题解析

价目表
每月用水量	单价
不超出6m³的部分	2元/m³
超出6m³ ，不超出10m³的部分	4元/m³
超出10m³的部分	8元/m³