浙江省金华市义乌三校联考2023-2024学年八年级第一学期数学期中试卷
试卷更新日期：2023-11-22 类型：期中考试
一、选择题（本大题共10小题，每小题3分）
-
1. 下列图形中，属于轴对称图形的是（ ）A、
B、
C、
D、
2. 以下列各组线段为边，能组成三角形的是（ ）A、2，3，4 B、2，3，5 C、2，5，10 D、8，4，43. 在数轴上表示不等式 ， 正确的是（ ）A、
B、
C、
D、
4. 能作为反例说明命题“若a＞﹣2，则a2＞4”是假命题的a的值可以为（ ）A、a＝3 B、a＝﹣3 C、a＝0 D、a＝﹣25. 如图，为测量池塘两端A、B的距离，小康在池塘外一块平地上选取了一点O ， 连接AO ， BO ， 并分别延长AO ， BO到点C ， D ， 使得AO＝DO ， BO＝CO ， 连接CD ， 测得CD的长为165米，则池塘两端A ， B之间的距离为（ ）
A、160米 B、165米 C、170米 D、175米6. 如图，已知△ABC ， 小慧同学利用尺规工具作出△A1B1C1与其全等，根据作图痕迹请判断小慧同学的全等判定依据（ ）
A、AAS B、SSS C、SAS D、ASA7. 在△ABC中，∠A＝∠B＝2∠C ， 则△ABC的形状是（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、形状无法确定8. 已知AD是△ABC中BC边上的中线，AB＝10，AC＝6，则AD的取值范围是（ ）A、4＜AD＜16 B、2＜AD＜8 C、4＜AD＜10 D、8≤AD≤169. 如图，把△ABC纸片沿DE折叠，当点C落在四边形ABDE的外部时，此时测得∠1＝120°，∠2＝40°，则∠C的度数为（ ）
A、40° B、50° C、60° D、80°10. 如图，Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F ， 则的面积为（ ）
A、 B、 C、 D、二、填空题（本大题共6小题，每小题4分）
-
11. 在△ABC中，∠A＝40°，∠B＝75°，则∠C的度数是度．12. 已知等腰三角形的一个内角为110°，则等腰三角形的底角的度数为.13. 若x＞y时，则x+2y+2（用不等式填空）．14. 如图，在△ABC中，∠B＝65°，∠C＝30°，分别以点A和点C为圆心，大于AC画弧，两弧相交于点M ， N ， 作直线MN ， 连接AD ， 则∠BAD的度数为 ．
15. 如图，在△ABC中，ED∥BC ， ∠ABC和∠ACB的平分线分别交ED于点G、F ， 若FG＝3，ED＝7，则EB+DC的值为 ．
16. 如图，折叠等腰三角形纸片ABC ， 使点C落在边AB上的点F处，折痕为DE ． 已知AB＝AC ， FD⊥BC ．
(1)、∠AFE＝度；(2)、如果AF＝3，BF＝5，则CE＝ ．三、解答题（本大题共7小题，其中17题6分，18-19题8分，20-21题10分，22-23题12分）
-
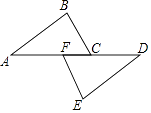
17. 如图，点A、F、C、D在同一条直线上，已知AF=DC，∠A=∠D，BC∥EF，求证：AB=DE．
18. 如图是由边长为1的小正方形组成的网格，△ABC的顶点都在格点上．请分别按下列要求完成解答：
(1)、画出△ABC的高AD ， 中线CE；(2)、画出将△ABC向右平移3格，再向上平移4格所得到的△A1B1C1；19. 如图所示，在△ABC中，CD⊥AB于点D ， AC＝4，BC＝3， ， 求CD ， BD的长.
20. 如图，在△ABC中，CF⊥AB于F ， BE⊥AC于E ， M为BC的中点，BC＝10．
(1)、求证：MF=ME；(2)、若∠ABC＝50°，∠ACB＝60°，求∠EMF的度数．21. 如图，△ABC和△DCE都是等腰直角三角形，CA＝CB，CD＝CE，且点D在△ABC的斜边AB上．
(1)、连结AE，求证：△ACE≌△BCD．(2)、若BD＝2，CD＝6，求AD的长．22. 如图，在Rt△ABC中，∠ACB＝90°，∠A＝60°，AC＝6，CD平分∠ACB ， 交边AB于点D ， 点E是边AB的中点．点P为边CB上的一个动点．
(1)、AE＝ ， ∠ACD＝度；(2)、当四边形ACPD为轴对称图形时，求BP的长；(3)、若△CPD是等腰三角形，求∠CPD的度数；(4)、若点M在线段CD上，连接MP、ME ， 直接写出MP+ME的值最小时CP的长度．23. 如图1，直线AM⊥AN ， AB平分∠MAN ， 过点B作BC⊥BA交AN于点C；动点E、D同时从A点出发，其中动点E以2cm/s的速度沿射线AN方向运动，动点D的运动速度为1cm/s；已知AC＝6cm ， 设动点D ， E的运动时间为t ．
(1)、试求AB的长；(2)、当点D在射线AM上运动时，满足S△ADB：S△BEC＝3：4，试求点D ， E的运动时间t的值；(3)、当动点D在直线AM上运动，点E在射线AN上运动时，是否存在某个时间t ， 使得△ADB与△BEC全等？若存在，请求出时间t的值；若不存在，请说出理由．