浙江省宁波市余姚市六校2023-2024学年八年级第一学期数学期中试卷
试卷更新日期:2023-11-22 类型:期中考试
一、选择题(每小题3分,共30分)
-
1. 在下列交通标志中,是轴对称图形的为( )A、
 B、
B、 C、
C、 D、
D、 2. 下列长度的三条线段,能组成三角形的是( )A、1,2,3 B、3,5,6 C、4,5,10 D、5,5,123. 若 , 则下列不等式正确的是( )A、 B、 C、 D、4. 能说明命题“对于任意实数 , 都有”是假命题的反例为( )A、 B、 C、 D、5. 下列各图中,正确画出AC边上的高的是( )A、
2. 下列长度的三条线段,能组成三角形的是( )A、1,2,3 B、3,5,6 C、4,5,10 D、5,5,123. 若 , 则下列不等式正确的是( )A、 B、 C、 D、4. 能说明命题“对于任意实数 , 都有”是假命题的反例为( )A、 B、 C、 D、5. 下列各图中,正确画出AC边上的高的是( )A、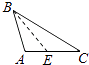 B、
B、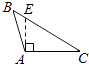 C、
C、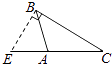 D、
D、 6. 如图,CD是Rt△ABC的中线,∠ACB=90°,∠ABC=25°,则∠ADC的度数为( )
6. 如图,CD是Rt△ABC的中线,∠ACB=90°,∠ABC=25°,则∠ADC的度数为( ) A、60° B、50° C、65° D、55°7. 如图,在△ABC和△DBE中,BE=BC,添加一个条件,不能证明△ABC≌△DBE的是( )
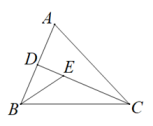
A、60° B、50° C、65° D、55°7. 如图,在△ABC和△DBE中,BE=BC,添加一个条件,不能证明△ABC≌△DBE的是( )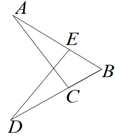 A、AB=DB B、∠A=∠D C、AC=DE D、∠ACB=∠DEB8. 如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A、AB=DB B、∠A=∠D C、AC=DE D、∠ACB=∠DEB8. 如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )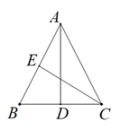 A、20° B、35° C、40° D、50°9. 如图,AB,BC,CD,DE是四根长度均为5cm的火柴棒,点A,C,E共线.若AC=6,CD⊥BC,则线段CE的长度是( )
A、20° B、35° C、40° D、50°9. 如图,AB,BC,CD,DE是四根长度均为5cm的火柴棒,点A,C,E共线.若AC=6,CD⊥BC,则线段CE的长度是( ) A、6cm B、7cm C、cm D、8cm10. 如图,在Rt△ABC中,∠ACB=90°,分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC,记四块阴影部分的面积分别为、、、.若已知 , 则下列结论:①;②;③;④ ,
A、6cm B、7cm C、cm D、8cm10. 如图,在Rt△ABC中,∠ACB=90°,分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC,记四块阴影部分的面积分别为、、、.若已知 , 则下列结论:①;②;③;④ ,其中正确的结论是( )
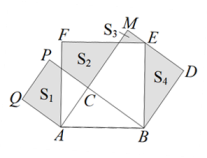 A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题(每小题4分,共24分)
-
11. 在△ABC中,∠A=45°,∠B=75°,则∠C的度数为.12. “与5的差大于的4倍”用不等式表示为.13. 若等腰三角形的一个内角为50°,则其顶角为.14. 如图,在△ABC中,CD是AB边上的高,BE平分∠ABC交CD于点E,BC=5.若△BCE的面积为5,则ED的长为.
 15. 如图,在长方形ABCD中,AB=8,BC=10,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为.
15. 如图,在长方形ABCD中,AB=8,BC=10,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为.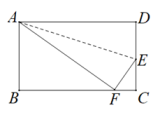 16. 如图,在边长为2的等边三角形中,点D,E分别是BC,AB的中点,点P是AD上一动点,则△PBE的周长最小值为.
16. 如图,在边长为2的等边三角形中,点D,E分别是BC,AB的中点,点P是AD上一动点,则△PBE的周长最小值为.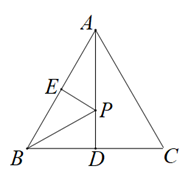
三、解答题(共66分)
-
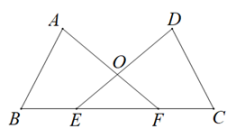
17. 已知:如图,点E,F在BC边上,BE=CF,∠AFE=∠DEC,∠B=∠C,AF与DE交于点O.求证:AB=DC.
 18. 如图,在方格纸中,每一个小正方形的边长为1,按要求画一个三角形,使它的顶点都在小正方形的顶点上.
18. 如图,在方格纸中,每一个小正方形的边长为1,按要求画一个三角形,使它的顶点都在小正方形的顶点上.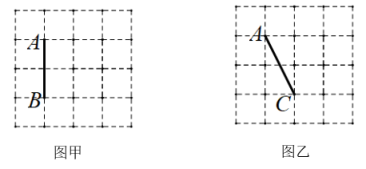 (1)、在图甲中画一个以AB为边且面积为3的直角三角形;(2)、在图乙中画一个使AC为腰的等腰三角形.19. 如图,在Rt△ABC中,∠ACB=90°
(1)、在图甲中画一个以AB为边且面积为3的直角三角形;(2)、在图乙中画一个使AC为腰的等腰三角形.19. 如图,在Rt△ABC中,∠ACB=90°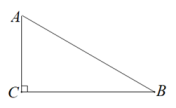 (1)、用直尺和圆规作∠BAC的平分线交BC于点D(保留作图痕迹);(2)、若AD=DB,求∠B的度数.20. 如图所示的一块草坪,∠ADC=90°,AD=4m,CD=3m,AB=13m,BC=12m.求这块草坪的面积.
(1)、用直尺和圆规作∠BAC的平分线交BC于点D(保留作图痕迹);(2)、若AD=DB,求∠B的度数.20. 如图所示的一块草坪,∠ADC=90°,AD=4m,CD=3m,AB=13m,BC=12m.求这块草坪的面积.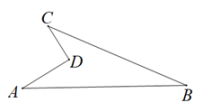 21. 如图,在△ABC中,∠ACB=90°,D,E分别是AB,BC的中点,CF//AB交DE的延长线于点F.
21. 如图,在△ABC中,∠ACB=90°,D,E分别是AB,BC的中点,CF//AB交DE的延长线于点F.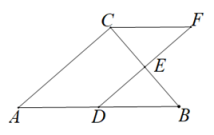 (1)、求证:FC=DB;(2)、若AC=8,CF=5.求BC的长.22. 如图,∠A=∠B,AE=BE,点D在AC边上,∠DEC=∠ADB,AE和BD相交于点O.
(1)、求证:FC=DB;(2)、若AC=8,CF=5.求BC的长.22. 如图,∠A=∠B,AE=BE,点D在AC边上,∠DEC=∠ADB,AE和BD相交于点O.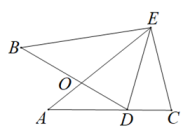 (1)、求证:△AEC≌△BED;(2)、若∠DEC=38°,求∠BDE度数.23. 如图,在Rt△ABC中,∠ACB=90°,AC=CB,D在BC边上,P,Q是射线AD上两点,且CP=CQ,∠PCQ=90°.
(1)、求证:△AEC≌△BED;(2)、若∠DEC=38°,求∠BDE度数.23. 如图,在Rt△ABC中,∠ACB=90°,AC=CB,D在BC边上,P,Q是射线AD上两点,且CP=CQ,∠PCQ=90°.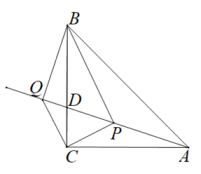 (1)、求证:AP=BQ;(2)、若CP=1,BP=.
(1)、求证:AP=BQ;(2)、若CP=1,BP=.①求AP的长;
②求△ABC的面积.
24. 定义:若以三条线段 , , 为边能构成一个直角三角形,则称线段 , , 是勾股线段组.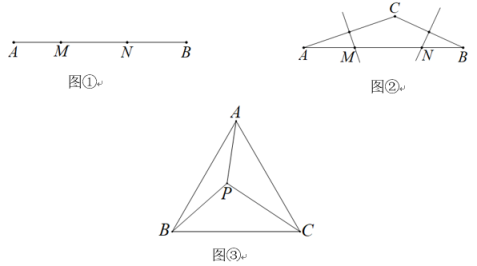 (1)、如图①,已知点M,N是线段AB上的点,线段AM,MN,NB是勾股线段组.若AB=12,AM=3,求MN的长;(2)、如图②,△ABC中,∠A=17°,∠B=28°,边AC,BC的垂直平分线分别交AB于点M,N,求证:线段AM,MN,NB是勾股线段组;(3)、如图③,在等边△ABC,P为△ABC内一点,线段AP,BP,CP构成勾股线段组,CP为此线段组的最长线段,求∠APB的度数.
(1)、如图①,已知点M,N是线段AB上的点,线段AM,MN,NB是勾股线段组.若AB=12,AM=3,求MN的长;(2)、如图②,△ABC中,∠A=17°,∠B=28°,边AC,BC的垂直平分线分别交AB于点M,N,求证:线段AM,MN,NB是勾股线段组;(3)、如图③,在等边△ABC,P为△ABC内一点,线段AP,BP,CP构成勾股线段组,CP为此线段组的最长线段,求∠APB的度数.