浙江省宁波市余姚市六校2023-2024学年九年级第一学期数学期中联考试卷
试卷更新日期:2023-11-22 类型:期中考试
一、选择题(本题共10小题,每小题3分,共30分.每小题只有一个选项是正确的,不选、多选、错选,均不给分)
-
1. 下列事件为必然事件的是( )A、三角形内角和是 B、打开电视机,正在播放新闻 C、明天下雨 D、掷一枚质地均匀的硬币,正面朝上2. 已知的半径是4,P点到圆心的距离为3,则P点与的位置关系是( )A、在圆外 B、在圆内 C、在圆上 D、无法确定3. 二次函数y=(x﹣2)2+3的最小值是( )A、2 B、3 C、﹣2 D、﹣34. 如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么B(﹣3,2)的对应点B′的坐标是( )
 A、(2,3) B、(3,2) C、(2,﹣3) D、(3,﹣2)5. 如图,在中, , , 则的度数是( )
A、(2,3) B、(3,2) C、(2,﹣3) D、(3,﹣2)5. 如图,在中, , , 则的度数是( ) A、40° B、30° C、20° D、10°6. 抛物线是由抛物线经过怎样的平移得到的( )A、向左平移个单位长度,向上平移个单位长度 B、向左平移个单位长度,向下平移个单位长度 C、向右平移个单位长度,向上平移个单位长度 D、向右平移个单位长度,向下平移个单位长度7. 如图,正六边形与正方形有重合的中心O , 若∠BOC是某个正n边形的一个外角,则n的值为( )
A、40° B、30° C、20° D、10°6. 抛物线是由抛物线经过怎样的平移得到的( )A、向左平移个单位长度,向上平移个单位长度 B、向左平移个单位长度,向下平移个单位长度 C、向右平移个单位长度,向上平移个单位长度 D、向右平移个单位长度,向下平移个单位长度7. 如图,正六边形与正方形有重合的中心O , 若∠BOC是某个正n边形的一个外角,则n的值为( ) A、8 B、10 C、12 D、168. 抛物线y=ax2+bx+c(a≠0)的图象如图所示,则下列说法正确的是( )
A、8 B、10 C、12 D、168. 抛物线y=ax2+bx+c(a≠0)的图象如图所示,则下列说法正确的是( )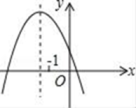 A、b2﹣4ac<0 B、abc<0 C、2a-b>0 D、a﹣b+c<09. 已知二次函数y=x2-2ax+a2-2a-4(a为常数)的图象与轴有交点,且当时,随的增大而增大,则a的取值范围是( )A、a≥-2 B、-2≤a≤3 C、-2≤a<3 D、a<310. 如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A、b2﹣4ac<0 B、abc<0 C、2a-b>0 D、a﹣b+c<09. 已知二次函数y=x2-2ax+a2-2a-4(a为常数)的图象与轴有交点,且当时,随的增大而增大,则a的取值范围是( )A、a≥-2 B、-2≤a≤3 C、-2≤a<3 D、a<310. 如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题共6小题,每小题4分,共24分)
-
11. 一个不透明布袋里只装有5个红球和3个白球(除颜色外其余都相同),则从中任意摸出一个球是红球的概率为 .12. 若函数是二次函数,则 .13. 如图,点A,B,C,D在上, , 则 .
 14. 如图,在平面直角坐标系中,弧ACB所在圆的圆心P的坐标为(3,4),弧ACB与x轴交于点(1,0),则⊙P与x轴的另一交点坐标是 .
14. 如图,在平面直角坐标系中,弧ACB所在圆的圆心P的坐标为(3,4),弧ACB与x轴交于点(1,0),则⊙P与x轴的另一交点坐标是 .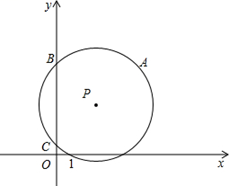 15. 如图,在中,为直径,点为圆上一点,将劣弧沿弦翻折交于点 , 连接 , 若点与圆心不重合, , 则的度数是 .
15. 如图,在中,为直径,点为圆上一点,将劣弧沿弦翻折交于点 , 连接 , 若点与圆心不重合, , 则的度数是 . 16. 二次函数的图像与
16. 二次函数的图像与 轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有个(提示:必要时可利用上面的备用图画出图象来分析).
轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有个(提示:必要时可利用上面的备用图画出图象来分析).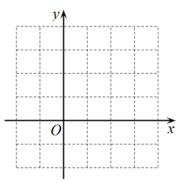
三、解答题(本题共8小题,共66分.解答应写出文字说明、证明过程或演算步骤)
-
17. 现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾,在分类后小王扔了一袋垃圾,小张扔了两袋垃圾.(1)、写出小王所扔的垃圾恰好是“厨余垃圾”的概率;(2)、求小张所扔的两袋垃圾不同类的概率用树状图或列表解决 .18. 如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.求残片所在圆的面积.
 19. 一名运动员在10米高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面的高度y(米)与离起跳点A的水平距离x(米)之间的函数关系如图所示,运动员离起跳点A的水平距离为1米时达到最高点,当运动员离起跳点A的水平距离为3米时离水面的距离为7米.
19. 一名运动员在10米高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面的高度y(米)与离起跳点A的水平距离x(米)之间的函数关系如图所示,运动员离起跳点A的水平距离为1米时达到最高点,当运动员离起跳点A的水平距离为3米时离水面的距离为7米. (1)、求y关于x的函数表达式;(2)、求运动员从起跳点到入水点的水平距离的长.20. 如图,是的直径,点C,D在上, .
(1)、求y关于x的函数表达式;(2)、求运动员从起跳点到入水点的水平距离的长.20. 如图,是的直径,点C,D在上, . (1)、求证:;(2)、若求的半径.21. 如图,直线y=x+m和抛物线y=x2+bx+c都经过点A、点B,且A(1,0),点C(0,3)是抛物线与y轴的交点.
(1)、求证:;(2)、若求的半径.21. 如图,直线y=x+m和抛物线y=x2+bx+c都经过点A、点B,且A(1,0),点C(0,3)是抛物线与y轴的交点. (1)、求两个函数的表达式;(2)、求点B的坐标;(3)、直接写出不等式x2+bx+3≥x+m的解集.22. 小军与小玲共同发明了一种“字母棋”,进行比胜负的游戏.她们用四种字母做成10只棋子,其中A棋1只,B棋2只,C棋3只,D棋4只.
(1)、求两个函数的表达式;(2)、求点B的坐标;(3)、直接写出不等式x2+bx+3≥x+m的解集.22. 小军与小玲共同发明了一种“字母棋”,进行比胜负的游戏.她们用四种字母做成10只棋子,其中A棋1只,B棋2只,C棋3只,D棋4只.
“字母棋”的游戏规则为:
①游戏时两人各摸一只棋进行比赛称一轮比赛,先摸者摸出的棋不放回;
②A棋胜B棋、C棋;B棋胜C棋、D棋;C棋胜D棋;D棋胜A棋;
③相同棋子不分胜负.
(1)、若小玲先摸,问小玲摸到C棋的概率是多少?(2)、已知小玲先摸到了C棋,小军在剩余的9只棋中随机摸一只,问这一轮中小玲胜小军的概率是多少?(3)、已知小玲先摸一只棋,小军在剩余的9只棋中随机摸一只,问这一轮中小玲希望摸到哪种棋胜小军的概率最大?23. 金秋十月,某景区以生态环境保护与绿色经济共赢的特色吸引各地游客纷纷前来观光.当地超市销售一批成本为20元/千克的绿色健康食品,深受游客青睐.经市场调查发现,该食品每天的销售量y(千克)与销售单价x(元/千克)之间满足一次函数关系,其图象如图所示. (1)、求该食品每天的销售量y(千克)与销售单价x(元/千克)之间的函数关系式;(2)、求出超市销售该食品每天的销售利润W(元)与销售单价x(元/千克)之间的函数表达式;(利润=销售额-销售成本)(3)、若超市按售价不低于成本价,且不高于40元销售,则销售单价定为多少,才能使销售该食品每天获得的利润W(元)最大?最大利润是多少?24. 在平面直角坐标系xOy中,已知点P(4,3),⊙O经过点P,过点P作x轴的平行线交⊙O于点E.
(1)、求该食品每天的销售量y(千克)与销售单价x(元/千克)之间的函数关系式;(2)、求出超市销售该食品每天的销售利润W(元)与销售单价x(元/千克)之间的函数表达式;(利润=销售额-销售成本)(3)、若超市按售价不低于成本价,且不高于40元销售,则销售单价定为多少,才能使销售该食品每天获得的利润W(元)最大?最大利润是多少?24. 在平面直角坐标系xOy中,已知点P(4,3),⊙O经过点P,过点P作x轴的平行线交⊙O于点E. (1)、如图1,求线段OP的长;(2)、点A为y轴正半轴上的一动点,点B和点A关于直线PE对称,连接PA,PB.直线PA,PB分别交⊙O于点C,D.直线CD交x轴于点F,交直线PE于点G.
(1)、如图1,求线段OP的长;(2)、点A为y轴正半轴上的一动点,点B和点A关于直线PE对称,连接PA,PB.直线PA,PB分别交⊙O于点C,D.直线CD交x轴于点F,交直线PE于点G.①点A运动到如图2位置,连接CE,DE.求证:∠DGP=ECP.
②在点A运动过程中,当DF=OP时,求点D的坐标.