山东省威海市文登区2023-2024学年九年级上学期期中联考数学(五四学制)

试卷更新日期：2023-11-21 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一个是正确的．每小题选对得3分，选错、不选或多选，均不得分）

1. 在函数 $y = \frac{1 - \sqrt{x}}{x - 3}$ 中，自变量x的取值范围是（）

A、 $x \geq 0$ B、 $x \neq 3$ C、 $x \geq 0 且 x \neq 3$ D、 $0 \leq x \leq 3$

查看试题解析
2. 如图，在平地上种植树木时，要求株距（相邻两棵树之间的水平距离）为 $5 m$ ．若在坡比为 $i = 1 ： 2.5$ 的山坡树，也要求株距为 $5 m$ ，那么相邻两棵树间的坡面距离（）

A、 $2.5 m$ B、 $5 m$ C、 $\sqrt{29} m$ D、 $10 m$

查看试题解析
3. 在△ABC中，∠A ， ∠B均为锐角，且 $| \tan B - \sqrt{3} |$ +(2sinA- $\sqrt{3}$ )²=0，则△ABC是（　　）

A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形

查看试题解析
4. 关于抛物线 $y = {(2 x - 1)}^{2} - 3$ ，下列说法错误的是（　　）

A、开口向上 B、顶点坐标为（1，－3） C、当x＞ $\frac{1}{2}$ 时，y随x的增大而增大 D、该抛物线与x轴有两个交点

查看试题解析
5. 已知抛物线 $y = x^{2} - 4 x + 3$ 与x轴相交于点A ， B（点A在点B左侧），顶点为M ．平移该抛物线，使点M平移后的对应点M'落在x轴上，点B平移后的对应点B'落在y轴上，则平移后的抛物线解析式为（　　）

A、 $y = x^{2} + 2 x + 1$ B、 $y = x^{2} + 2 x - 1$ C、 $y = x^{2} - 2 x + 1$ D、 $y = x^{2} - 2 x - 1$

查看试题解析
6.
如图，△ABC的顶点是正方形网格的格点，则sinA的值为（　　）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{\sqrt{10}}{10}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
7. 二次函数 $y = a x^{2} + b x$ 和反比例函数 $y = \frac{b}{x}$ 在同一直角坐标系中的大致图象是（）

A、 B、 C、 D、

查看试题解析
8. 二次函数 $y = a x^{2} + | b | x + c$ ，其对称轴为 $x = - 1$ ，若 $(- \frac{14}{3} ， y_{1})$ ， $(\frac{5}{2} ， y_{2})$ ， $(3 ， y_{3})$ 是拋物线上三点，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{3} < y_{1} < y_{2}$ C、 $y_{3} < y_{2} < y_{1}$ D、 $y_{2} < y_{1} < y_{3}$

查看试题解析
9. 为预防新冠病毒，某学校每周末用药熏消毒法对教室进行消毒，已知药物释放过程中，教室内每立方米空气中含药量 $y (mg)$ 与时间 $t (h)$ 成正比例；药物释放完毕后， $y$ 与 $t$ 成反比例，如图所示．根据图象信息，下列选项错误的是（）

A、药物释放过程需要 $\frac{3}{2}$ 小时 B、药物释放过程中， $y$ 与 $t$ 的函数表达式是 $y = \frac{2}{3} t$ C、空气中含药量大于等于 $0.5 {mg/m}^{3}$ 的时间为 $\frac{9}{4} h$ D、若当空气中含药量降低到 $0.25 {mg/m}^{3}$ 以下时对身体无害，那么从消毒开始，至少需要经过4.5小时学生才能进入教室

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c$ （ $a$ ， $b$ ， $c$ 是常数， $a \neq 0$ ）的 $y$ 与 $x$ 的部分对应值如下表：
$x$
…
$- 5$
$- 4$
$- 2$
$0$
$2$
…
$y$
…
$6$
$0$
$- 6$
$- 4$
$6$
…
有下列结论：① $a > 0$ ；② 当 $x = - 2$ 时，函数的最小值为 $- 6$ ；③ 若点 $(- 8 ， y_{1})$ ，点 $(8 ， y_{2})$ 在该二次函数图象上，则 $y_{1} < y_{2}$ ；④ 方程 $a x^{2} + b x + c = - 5$ 有两个不相等的实数根．其中，正确结论的个数是（）

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分，只要求填出最后结果）

11. 抛物线 $y = (k - 1) x^{2} - x + 1$ 与x轴有交点，则k的取值范围是.

查看试题解析
12. 如图，点A是反比例函数y $= \frac{6}{x}$ （x＞0）上的一点，过点A作AC⊥y轴，垂足为点C ， AC交反比例函数y＝ $\frac{2}{x}$ 的图象于点B ，点P是x轴上的动点，则△PAB的面积为

查看试题解析
13. 竖直向上抛出小球的高度h（米）与抛出的时间t（秒）满足关系式 $h = - 4.9 t^{2} + 24.5 t$ ，从地面相隔1秒竖直向上分别抛出的两个小球，当两个小球在空中处于同一个高度时，这个高度离地面米．

查看试题解析
14. 如图，在矩形ABCD中，点E在DC上，将矩形沿AE折叠，使点D落在BC边上的点F处．若AB＝3，BC＝5，则tan∠DAE的值为.

查看试题解析
15. 如图，点A ， B的坐标分别为（1，4）和（4，4），抛物线y＝a（x-m）²+n的顶点在线段AB上运动，与x轴交于C、D两点（C在D的左侧），点C的横坐标最小值为-3，则点D的横坐标最大值为．

查看试题解析
16. 如图，已知在平面直角坐标系中，点A在x轴负半轴上，点B在第二象限内，反比例函数 $y = \frac{k}{x}$ 的图象经过△OAB的顶点B和边AB的中点C ，如果△OAB的面积为6，那么k的值是．

查看试题解析

三、解答题（本大题共8小题，共72分）

17. 计算： ${(2022 - π)}^{0} - 4 c o s 30 ° + 4 t a n 45 ° - | 3 - \sqrt{12} |$

查看试题解析
18. 如图，在平面直角坐标系xOy中，一次函数y＝kx+b的图象与反比例函数y $= \frac{m}{x}$ 的图象交于A（2，3）、B（-3，n）两点．

(1)、求一次函数和反比例函数的解析式；

(2)、观察图象，直接写出不等式 $\frac{m}{x} >$ kx+b的解集；

(3)、若P是y轴上一点，且满足△PAB的面积是5，求点P坐标．

查看试题解析
19. 某农场计划建造一个矩形养殖场，为充分利用现有资源，该矩形养殖场一面靠墙（墙的长度为10m），另外三面用栅栏围成，中间再用栅栏把它分成两个面积为1：2的矩形，已知栅栏的总长度为24m，设较小矩形的宽为xm（如图）.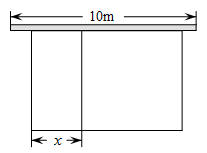

(1)、若矩形养殖场的总面积为36 $m^{2}$ ，求此时x的值；

(2)、当x为多少时，矩形养殖场的总面积最大？最大值为多少？

查看试题解析
20. 一次数学活动课上，老师带领学生去测一条东西流向的河宽，如图所示，小明在河北岸点A处观测到河对岸有一点C在A的南偏西60°的方向上，沿河岸向西前行20m到达B处，又测得C在B的南偏西45°的方向上，请你根据以上数据，帮助小明计算出这条河的宽度．（结果保留根号）

查看试题解析
21. 如图，在△ABC中，AD是BC边上的高，AE是BC边上的中线，∠C=45°，sinB= $\frac{1}{3}$ ，AD=1．

(1)、求BC的长；

(2)、求tan∠DAE的值．

查看试题解析
22. 如图，点A在双曲线 $y = \frac{3}{x}$ （ $x > 0$ ）上，过点A作 AC⊥x轴，垂足为C ．线段OA的垂直平分线BD交OC ， OA于点B ， D ， △ABC的周长为4，求点A的坐标．

查看试题解析
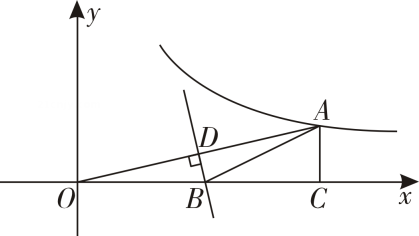23. 某商场经营某种品牌的玩具，购进时的单价是 $30$ 元，根据市场调查：在一段时间内，销售单价是 $40$ 元时，销售量是 $600$ 件，而销售单价每涨 $1$ 元，就会少售出 $10$ 件玩具.

(1)、不妨设该种品牌玩具的销售单价为 $x$ 元 $(x > 40)$ ，请你分别用 $x$ 的代数式来表示销售量 $y$ 件和销售该品牌玩具获得利润 $w$ 元，

(2)、在（1）问条件下，若商场获得了 $10000$ 元销售利润，求该玩具销售单价 $x$ 应定为多少

(3)、在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于 $44$ 元，且商场要完成不少于 $540$ 件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？

查看试题解析
24. 如图，在平面直角坐标系中，二次函数的图象交坐标轴于A（-1，0），B（4，0），C（0，-4）三点，点P是直线BC下方抛物线上一动点．

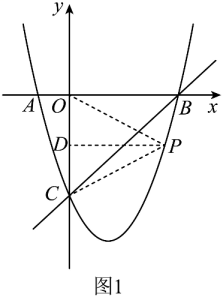(1)、求这个二次函数的解析式；

(2)、是否存在点P ，使△POC是以OC为底边的等腰三角形？若存在，求出P点坐标；若不存在，请说明理由；

(3)、动点P运动到什么位置时，△PBC面积最大，求出此时P点坐标和△PBC的最大面积．

查看试题解析

$x$	…	$- 5$	$- 4$	$- 2$	$0$	$2$	…
$y$	…	$6$	$0$	$- 6$	$- 4$	$6$	…