山东省威海市文登区2023-2024学年七年级上学期期中联考数学(五四学制)
试卷更新日期:2023-11-21 类型:期中考试
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分)
-
1. 下面四个图形中,属于轴对称图形的是( )A、
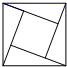 B、
B、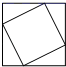 C、
C、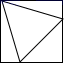 D、
D、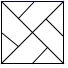 2. 如图,人字梯中间一般会设计一“拉杆”,这样做的道理是( )
2. 如图,人字梯中间一般会设计一“拉杆”,这样做的道理是( ) A、两点之间,线段最短 B、垂线段最短 C、两直线平行,内错角相等 D、三角形具有稳定性3. 现有两根木棒,它们的长分别是20cm和30cm,若不改变现有木棒的长短,要钉成一个三角形木架,第三根木棒的长度可以是( )A、10cm B、40cm C、50cm D、60cm4. 如图,在△ABC中,AD平分∠BAC , AE是高,若∠B=40°,∠C=60°,则∠EAD的度数为( )
A、两点之间,线段最短 B、垂线段最短 C、两直线平行,内错角相等 D、三角形具有稳定性3. 现有两根木棒,它们的长分别是20cm和30cm,若不改变现有木棒的长短,要钉成一个三角形木架,第三根木棒的长度可以是( )A、10cm B、40cm C、50cm D、60cm4. 如图,在△ABC中,AD平分∠BAC , AE是高,若∠B=40°,∠C=60°,则∠EAD的度数为( ) A、30° B、10° C、40° D、20°5. 如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D , 交BC于点E . 若∠C=15°,EC=8,则△AEC的面积为( )
A、30° B、10° C、40° D、20°5. 如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D , 交BC于点E . 若∠C=15°,EC=8,则△AEC的面积为( ) A、32 B、16 C、64 D、1286. 对于下列说法:
A、32 B、16 C、64 D、1286. 对于下列说法:①角平分线上任意一点到角两边的距离相等;
②等腰三角形的高、中线、角平分线互相重合;
③三角形三边中垂线的交点到三个顶点的距离相等;
④直角三角形只有一条高线.
正确的有( )
A、①②③④ B、①③ C、①②③ D、①②④7. 如图,在△ABC 中,AB=AC,∠C=70°,△AB'C'与△ABC 关于直线 EF对称,点A在EF上,∠CAF=10°,连接BB' , 则∠ABB'的度数是( ) A、30° B、35° C、45° D、40°8. 如图,圆柱的高为8cm,底面半径为cm,一只蚂蚁从点A沿圆柱外壁爬到点B处吃食,要爬行的最短路程是( )
A、30° B、35° C、45° D、40°8. 如图,圆柱的高为8cm,底面半径为cm,一只蚂蚁从点A沿圆柱外壁爬到点B处吃食,要爬行的最短路程是( ) A、6cm B、8cm C、10cm D、12cm9. 如图,在中,分别是的中点,若的面积为1,则的面积是( )
A、6cm B、8cm C、10cm D、12cm9. 如图,在中,分别是的中点,若的面积为1,则的面积是( ) A、3 B、4 C、8 D、1210. 我国古代用勾、股、弦表示直角三角形的两条直角边和斜边.如图,由四个全等的直角三角形和一个小正方形拼成一个大正方形,数学家邹元治利用该图证明了勾股定理.已知大正方形面积为9,小正方形面积为5,则每个直角三角形中勾与股的差的平方为( )
A、3 B、4 C、8 D、1210. 我国古代用勾、股、弦表示直角三角形的两条直角边和斜边.如图,由四个全等的直角三角形和一个小正方形拼成一个大正方形,数学家邹元治利用该图证明了勾股定理.已知大正方形面积为9,小正方形面积为5,则每个直角三角形中勾与股的差的平方为( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题(本大题共6小题,每小题3分,共18分,只要求填出最后结果)
-
11. 如图,点A , B , C , D在同一条直线上,△ACE≌△DBF , AD=6,BC=2,则AC=.
 12. 如图,在△ABC中,∠B与∠C的平分线交于点P . 若∠BPC=108°,则∠A的度数为 .
12. 如图,在△ABC中,∠B与∠C的平分线交于点P . 若∠BPC=108°,则∠A的度数为 . 13. 如图,在△ABC中,∠C= , AD 平分∠BAC , AB=10cm,△ABD的面积为20cm2 , 则CD的长为cm.
13. 如图,在△ABC中,∠C= , AD 平分∠BAC , AB=10cm,△ABD的面积为20cm2 , 则CD的长为cm. 14. 如图,有一块农家菜地的平面图,其中AD=4,CD=3,AB=13,BC=12,∠ADC=90°,则这块菜地的面积为 .
14. 如图,有一块农家菜地的平面图,其中AD=4,CD=3,AB=13,BC=12,∠ADC=90°,则这块菜地的面积为 . 15. 如图,△ABC中,AB=AC,AD⊥BC于D点,DE⊥AB于点E,BF⊥AC于点F,DE=3cm,则BF=cm.
15. 如图,△ABC中,AB=AC,AD⊥BC于D点,DE⊥AB于点E,BF⊥AC于点F,DE=3cm,则BF=cm. 16. 如图,在△ABC中,AD⊥BC , CE⊥AB , 垂足分别为D , E , AD , CE交于点H , EH=EB=5,AH=13,则CH的长度为 .
16. 如图,在△ABC中,AD⊥BC , CE⊥AB , 垂足分别为D , E , AD , CE交于点H , EH=EB=5,AH=13,则CH的长度为 .
三、解答题
-
17. 一个缺角的三角形残片如图所示,请用尺规在残片图左侧的空白处,画出残片图复原后的完整三角形.(要求:保留作图痕迹,不写作法.)
 18. 如图,△ABC是等边三角形,D是AC上一点,BD=CE , ∠1=∠2,试判断BC与AE的位置关系,并写明理由.
18. 如图,△ABC是等边三角形,D是AC上一点,BD=CE , ∠1=∠2,试判断BC与AE的位置关系,并写明理由. 19. 明朝数学家程大位在《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地.送行二步与人起,五尺人高曾记.仕女佳人蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”
19. 明朝数学家程大位在《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地.送行二步与人起,五尺人高曾记.仕女佳人蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”翻译成现代文为:如图,秋千细索OA悬挂于O点,静止时竖直下垂,A点为踏板位置,踏板离地高度为一尺(AC=1尺).将它往前推进两步(EB⊥OC于点E , 且EB=10尺),踏板升高到点B位置,此踏板离地五尺(BD=5尺),求秋千绳索(OA或OB)的长度.
 20.
20.如图,由边长均为1个单位的小正方形组成的网格图中,点A , B , C都在格点上.
 (1)、△ABC的面积为;(2)、以AC为边画出一个与△ABC全等的三角形,并进一步探究:满足条件的三角形可以作出个;(3)、在直线l上确定点P , 使PB+PC的长度最短.(画出示意图,并标明点P的位置即可)21. 有一辆载有集装箱的卡车,高2.5米,宽1.6米,要开进如图所示的上边是半圆,下边是长方形的桥洞,已知半圆的直径为2米,长方形的另一条边长是2.3米,这辆卡车能否通过此桥洞?通过计算说明理由.
(1)、△ABC的面积为;(2)、以AC为边画出一个与△ABC全等的三角形,并进一步探究:满足条件的三角形可以作出个;(3)、在直线l上确定点P , 使PB+PC的长度最短.(画出示意图,并标明点P的位置即可)21. 有一辆载有集装箱的卡车,高2.5米,宽1.6米,要开进如图所示的上边是半圆,下边是长方形的桥洞,已知半圆的直径为2米,长方形的另一条边长是2.3米,这辆卡车能否通过此桥洞?通过计算说明理由.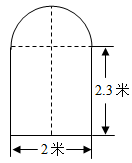 22. 在△ABC中,AB=AC , 点D是BC的中点,点E是AD上任意一点.
22. 在△ABC中,AB=AC , 点D是BC的中点,点E是AD上任意一点. (1)、如图1,连接BE , CE , BE与CE是否相等?并写明理由;(2)、如图2,若∠BAC=45°,BE的延长线与AC垂直相交于点F时,EF与CF是否相等?并写明理由.
(1)、如图1,连接BE , CE , BE与CE是否相等?并写明理由;(2)、如图2,若∠BAC=45°,BE的延长线与AC垂直相交于点F时,EF与CF是否相等?并写明理由.

