【备考2024】2023年高考数学新高考Ⅱ卷真题变式分层精准练:第20题
试卷更新日期:2023-11-21 类型:二轮复习
一、原题
-
1. 如图,三棱锥中,60°,E为BC中点.
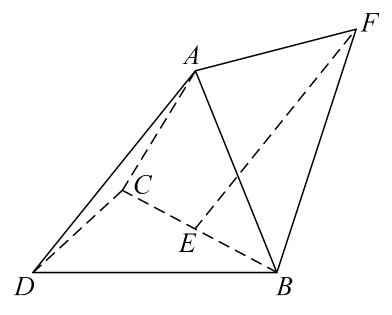 (1)、证明:(2)、点F满足 ,求二面角D-AB-F的正弦值.
(1)、证明:(2)、点F满足 ,求二面角D-AB-F的正弦值.二、基础
-
2. 如图,在三棱锥中, , 设点为上的动点.
 (1)、求面积的最小值;(2)、求平面与平面的夹角的余弦值.3. 如图,在四棱锥中,底面ABCD为平行四边形, , 侧面底面ABCD, , 且二面角的大小是 .
(1)、求面积的最小值;(2)、求平面与平面的夹角的余弦值.3. 如图,在四棱锥中,底面ABCD为平行四边形, , 侧面底面ABCD, , 且二面角的大小是 .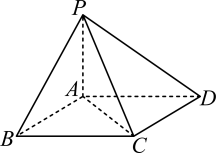 (1)、证明:;(2)、求二面角的正弦值.4. 如图,已知四棱锥中, , 是面积为的等边三角形且 , .
(1)、证明:;(2)、求二面角的正弦值.4. 如图,已知四棱锥中, , 是面积为的等边三角形且 , . (1)、证明:;(2)、求平面与平面所成角的余弦值.5. 已知四棱锥中,底面为直角梯形,平面 , , , , , M为中点,过C,D,M的平面截四棱锥所得的截面为 .
(1)、证明:;(2)、求平面与平面所成角的余弦值.5. 已知四棱锥中,底面为直角梯形,平面 , , , , , M为中点,过C,D,M的平面截四棱锥所得的截面为 .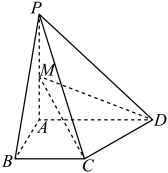 (1)、若与棱交于点F,画出截面 , 保留作图痕迹(不用说明理由),求点F的位置;(2)、求平面与平面所成锐二面角的余弦值.6. 如图,在四棱台中,底面是菱形, , 平面 .
(1)、若与棱交于点F,画出截面 , 保留作图痕迹(不用说明理由),求点F的位置;(2)、求平面与平面所成锐二面角的余弦值.6. 如图,在四棱台中,底面是菱形, , 平面 . (1)、若点是的中点,求证:平面;(2)、棱上是否存在一点 , 使得二面角的余弦值为若存在,求线段的长;若不存在,请说明理由.7. 如图,在三棱台ABC—中, , 平面平面
(1)、若点是的中点,求证:平面;(2)、棱上是否存在一点 , 使得二面角的余弦值为若存在,求线段的长;若不存在,请说明理由.7. 如图,在三棱台ABC—中, , 平面平面 (1)、证明:平面;(2)、若二面角的大小是 , 求线段的长.8. 如图,在三棱锥中,和均是以边长为的等边三角形,且 .
(1)、证明:平面;(2)、若二面角的大小是 , 求线段的长.8. 如图,在三棱锥中,和均是以边长为的等边三角形,且 . (1)、证明:平面PAC平面ABC;(2)、若点M在线段BC上,且 , 求二面角的余弦值.9. 如图1,在五边形中,四边形为正方形, , , 如图2,将沿折起,使得至处,且 .
(1)、证明:平面PAC平面ABC;(2)、若点M在线段BC上,且 , 求二面角的余弦值.9. 如图1,在五边形中,四边形为正方形, , , 如图2,将沿折起,使得至处,且 . (1)、证明:平面 .(2)、求二面角的余弦值.10. 如图,在四棱锥中,平面平面ABCD,平面平面ABCD.
(1)、证明:平面 .(2)、求二面角的余弦值.10. 如图,在四棱锥中,平面平面ABCD,平面平面ABCD. (1)、求证:平面ABCD;(2)、设 , , , 平面PBC与平面PCD的夹角的余弦值为 , 求BC的长.11. 如图,在四棱锥中,底面为梯形, , , , , 平面平面 , 为棱上的点,且 .
(1)、求证:平面ABCD;(2)、设 , , , 平面PBC与平面PCD的夹角的余弦值为 , 求BC的长.11. 如图,在四棱锥中,底面为梯形, , , , , 平面平面 , 为棱上的点,且 . (1)、求证:平面;(2)、若 , 二面角为 , 求平面与平面的夹角的余弦值.12. 如图,在直三棱柱中,底面是等腰直角三角, , 为侧棱的中点.
(1)、求证:平面;(2)、若 , 二面角为 , 求平面与平面的夹角的余弦值.12. 如图,在直三棱柱中,底面是等腰直角三角, , 为侧棱的中点. (1)、求证:平面;(2)、求二面角的正弦值.13. 如图,多面体是由棱长为3的正方体沿平面截去一角所得到,在棱上取一点E,过点 , C,E的平面交棱于点F.
(1)、求证:平面;(2)、求二面角的正弦值.13. 如图,多面体是由棱长为3的正方体沿平面截去一角所得到,在棱上取一点E,过点 , C,E的平面交棱于点F. (1)、求证:;(2)、若 , 求点E到平面的距离以及与平面所成角的大小.14. 如图,在直三棱柱中,是的中点.
(1)、求证:;(2)、若 , 求点E到平面的距离以及与平面所成角的大小.14. 如图,在直三棱柱中,是的中点.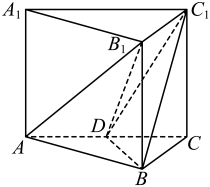 (1)、证明:平面.(2)、若 , 求二面角的余弦值.
(1)、证明:平面.(2)、若 , 求二面角的余弦值.三、提升
-
15. 如图所示,在直角三角形中, , , 将沿折起到的位置,使平面平面 , 点满足.
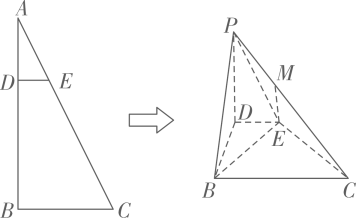 (1)、证明:;(2)、求二面角的余弦值.16. 如图,在多面体ABCDEF中,四边形ABCD与ABEF均为直角梯形,平面平面ABEF, .
(1)、证明:;(2)、求二面角的余弦值.16. 如图,在多面体ABCDEF中,四边形ABCD与ABEF均为直角梯形,平面平面ABEF, . (1)、已知点G为AF上一点,且AG=1,求证:平面DCE;(2)、已知直线BF与平面DCE所成角的正弦值为 , 求平面DCE与平面BDF所成锐二面角的余弦值.17. 在四棱锥中,底面为梯形,为上的点,且.
(1)、已知点G为AF上一点,且AG=1,求证:平面DCE;(2)、已知直线BF与平面DCE所成角的正弦值为 , 求平面DCE与平面BDF所成锐二面角的余弦值.17. 在四棱锥中,底面为梯形,为上的点,且.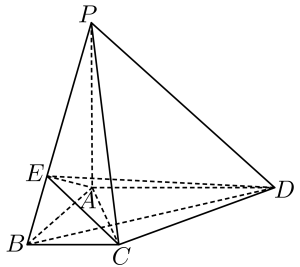 (1)、证明:面:(2)、若面 , 面面 , 求二面角的正弦值.18. 如图,在三棱柱中,所有棱长均为2,且 , , .
(1)、证明:面:(2)、若面 , 面面 , 求二面角的正弦值.18. 如图,在三棱柱中,所有棱长均为2,且 , , . (1)、证明:平面平面 .(2)、求平面ACD与平面夹角的余弦值.19. 在三棱锥中,底面ABC是边长为4的正三角形,侧面底面ABC, , , 点E在线段SB上,且 .
(1)、证明:平面平面 .(2)、求平面ACD与平面夹角的余弦值.19. 在三棱锥中,底面ABC是边长为4的正三角形,侧面底面ABC, , , 点E在线段SB上,且 .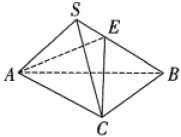 (1)、证明:平面ACE;(2)、求二面角的正弦值.20. 在三棱柱中, , , .
(1)、证明:平面ACE;(2)、求二面角的正弦值.20. 在三棱柱中, , , . (1)、证明:;(2)、若 , , 求平面与平面夹角的余弦值.21. 如图,在三棱柱中, , D是中点, .
(1)、证明:;(2)、若 , , 求平面与平面夹角的余弦值.21. 如图,在三棱柱中, , D是中点, .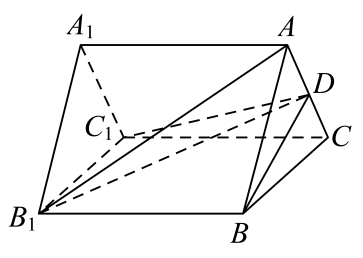 (1)、证明:;(2)、若 , , 且三棱柱的体积为 , 求二面角的余弦值.22. 如图,在三棱台中,.
(1)、证明:;(2)、若 , , 且三棱柱的体积为 , 求二面角的余弦值.22. 如图,在三棱台中,. (1)、求证:平面平面;(2)、若四面体的体积为2,求二面角的余弦值.23. 如图,在多面体中, , 平面 , 为等边三角形, , , , 点是的中点.
(1)、求证:平面平面;(2)、若四面体的体积为2,求二面角的余弦值.23. 如图,在多面体中, , 平面 , 为等边三角形, , , , 点是的中点. (1)、若点是的重心,证明;点在平面内;(2)、求二面角的正弦值.24. 如图,在圆锥中,是底面的直径,是底面圆周上的一点,且 , , , 是的中点.
(1)、若点是的重心,证明;点在平面内;(2)、求二面角的正弦值.24. 如图,在圆锥中,是底面的直径,是底面圆周上的一点,且 , , , 是的中点. (1)、求证:平面平面;(2)、求二面角的余弦值.25. 如图,在四棱锥中, , , , △是边长为2的等边三角形,平面平面 , 为线段上一点.
(1)、求证:平面平面;(2)、求二面角的余弦值.25. 如图,在四棱锥中, , , , △是边长为2的等边三角形,平面平面 , 为线段上一点. (1)、设平面平面 , 证明:平面;(2)、是否存在这样点 , 使平面与平面所成角为 , 如果存在,求的值;如果不存在,请说明理由.
(1)、设平面平面 , 证明:平面;(2)、是否存在这样点 , 使平面与平面所成角为 , 如果存在,求的值;如果不存在,请说明理由.四、培优
-
26. 如图,在几何体中,矩形所在平面与平面互相垂直,且 , , .
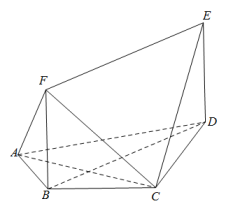 (1)、求证:平面;(2)、求二面角的平面角的余弦值.27. 如图,直三棱柱中, , , .
(1)、求证:平面;(2)、求二面角的平面角的余弦值.27. 如图,直三棱柱中, , , . (1)、证明:平面;(2)、若 , 求二面角的余弦值.28. 如图1,圆的内接四边形ABCD中, , , 直径 . 将圆沿AC折起,并连接OB、OD、BD,使得△BOD为正三角形,如图2.
(1)、证明:平面;(2)、若 , 求二面角的余弦值.28. 如图1,圆的内接四边形ABCD中, , , 直径 . 将圆沿AC折起,并连接OB、OD、BD,使得△BOD为正三角形,如图2. (1)、证明:图2中的平面BCD;(2)、在图2中,求二面角的余弦值.29. 如图,在四棱锥中,底面ABCD是边长为4的正方形,E为PA的中点,过E与底面ABCD平行的平面与棱PC,PD分别交于点G,F,M在线段AE上,且 .
(1)、证明:图2中的平面BCD;(2)、在图2中,求二面角的余弦值.29. 如图,在四棱锥中,底面ABCD是边长为4的正方形,E为PA的中点,过E与底面ABCD平行的平面与棱PC,PD分别交于点G,F,M在线段AE上,且 . (1)、求证:BG//平面;(2)、若PA⊥平面ABCD,且 , 求平面CFM与平面PCD所成锐二面角的余弦值.
(1)、求证:BG//平面;(2)、若PA⊥平面ABCD,且 , 求平面CFM与平面PCD所成锐二面角的余弦值.
-

