【备考2024】2023年高考数学新高考Ⅱ卷真题变式分层精准练:第17题
试卷更新日期:2023-11-21 类型:二轮复习
一、原题
-
1. 记△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为D为BC的中点,且AD=1.(1)、若求tanB;(2)、若 , 求b,c.
二、基础
-
2. 已知中角所对的边分别为 , 且满足.(1)、求角;(2)、若的面积是边上的点,且 , 求.3. 在中, .(1)、求;(2)、再从下列三个条件中,选择两个作为已知,使得存在且唯一,求的面积.
条件①:;条件②:;条件③:AB边上的高为 .
注:如果选择多个符合要求的条件分别解答,接第一个解答计分.
4. 在中,内角 , , 的对边分别是 , , , 且满足B.(1)、求角的值.(2)、 , , 求的面积.5. 在中,内角 , , 所对的边分别为 , , , 且 .(1)、证明:;(2)、若 , 且的面积为 , 求 .6. 在中,内角 , , 所对的边分别为 , , , 已知 .(1)、若 , , 求的值;(2)、若 , 求角 , 的大小.7. 在中,内角所对的边分别为 , 已知 , 且.(1)、求的值;(2)、求的面积;8. 在中,角A , B , C所对的边分别为a , b , c.已知.(1)、求角A的大小;(2)、若 , , AD是△ABC的角平分线,求AD的长.9. 已知在 中, , 分别是角 所对的边.(1)、求 ;(2)、若 , ,求 的面积.10. 在中,设角A,B,C的对边长分别为a,b,c.(1)、若 , , , 求的周长;(2)、若点D是边上一点,且 , , , 求的长.11. 如图,在中,内角A,B,C的对边分别为a,b,c, , .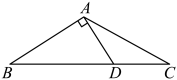 (1)、求;(2)、过点A作 , 交线段于点 , 且 , 求 .12. 记的内角A、B、C的对边分别为a、b、c,且 .(1)、求角的大小;(2)、设边上的高 , 求面积的最小值.
(1)、求;(2)、过点A作 , 交线段于点 , 且 , 求 .12. 记的内角A、B、C的对边分别为a、b、c,且 .(1)、求角的大小;(2)、设边上的高 , 求面积的最小值.三、提升
-
13. 在中,角所对的边分别是 , 且 .(1)、求角的大小;(2)、若是锐角三角形,求的面积的取值范围.14. 的内角A , B , C所对边分别为a , b , c , 点O为的内心,记 , , 的面积分别为 , , , 已知 , .(1)、在①;②;③中选一个作为条件,判断是否存在,若存在,求出的周长,若不存在,说明理由.(注:如果选择多个条件分别解答,按第一个解答计分.)(2)、若为锐角三角形,求面积的取值范围.15. 已知的内角的对边分别为 , , 平分交于点 , 且 .(1)、求;(2)、求的面积.16. 已知函数的周期为 , 且图像经过点 .(1)、求函数的单调递增区间(2)、在中,角 , , 所对的边分别是 , , , 若 , , , 求的值.17. 在①;②③这三个条件中选一个,补充在下面问题中,并加以解答.
问题:在中,角A,B,C所对的边分别为a,b,c,已知 , 解三角形.
18. 在中,为的角平分线,且.(1)、若 , , 求的面积;(2)、若 , 求边的取值范围.19. 在中,角所对的边分别为.(1)、求;(2)、若 , 过作垂直于交于点为上一点,且 , 求的最大值.20. 在中,内角A , B , C所对的边分别为a , b , c , 已知.(1)、求角A的大小;(2)、若 , 求周长的取值范围.21. 中,角 , , 所对的边分别是 , , , 满足: ,(1)、求角;(2)、若 , 求的取值范围.22. 已知的内角A,B,C的对边分别为a,b,c, .(1)、求A的值;(2)、若 , BE为边AC的高,AD为边BC的中线,求的值.23. 在①;②;③;这三个条件中任选一个(注:如果选择多个条件分别解答,按第一个解答计分)补充在下面问题中,并作答.在中,内角A,B,C的对边分别是a,b,c,且____.
(1)、求角的大小;(2)、若点满足 , , , 求的面积.24. 已知的内角 , , 的对边分别为 , , , .(1)、求;(2)、若 , 求边上的中线的最大值.四、培优
-
25. 在中,角的对边分别为 , 且.(1)、求的值;(2)、若 , 从下列三个条件中选出一个条件作为已知,使得存在且唯一确定,求的面积.
条件①:;条件②:;条件③:的周长为9.
26. 已知的内角 , , 的对边分别为 , , , 且.(1)、求角的大小;(2)、若的中点为且 , 求的最大值.27. 在中, , 点D在边上, , 且. (1)、若的面积为 , 求;(2)、设 , 若 , 求.28. 上海花博会的成功举办离不开对展览区域的精心规划.如图所示,将展区中扇形空地分隔成三部分建成花卉观赏区,分别种植玫瑰花、白玉兰和菊花.知扇形的半径为米, , 动点在扇形的弧上,点在半径上,且.
(1)、若的面积为 , 求;(2)、设 , 若 , 求.28. 上海花博会的成功举办离不开对展览区域的精心规划.如图所示,将展区中扇形空地分隔成三部分建成花卉观赏区,分别种植玫瑰花、白玉兰和菊花.知扇形的半径为米, , 动点在扇形的弧上,点在半径上,且.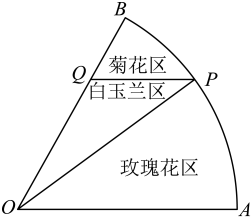 (1)、当米时,求分隔栏的长;(2)、综合考虑到成本和美观等原因,希望使白玉兰种植区的面积尽可能的大,求该种植区三角的面积的最大值.
(1)、当米时,求分隔栏的长;(2)、综合考虑到成本和美观等原因,希望使白玉兰种植区的面积尽可能的大,求该种植区三角的面积的最大值.
-