【备考2024】2023年高考数学新高考Ⅱ卷真题变式分层精准练：第14题

试卷更新日期：2023-11-21 类型：二轮复习

进入出卷网下载

一、原题

1. 底面边长为4的正四棱锥被平行于其底面的平面所截，截去一个底面边长为2，高为3的正四棱锥，所得棱台的体积为 .

查看试题解析

二、基础

2. 中国某些地方举行婚礼时要在吉利方位放一张桌子，桌子上放一个装满粮食的升斗，斗面用红纸糊住，斗内再插一杆秤、一把尺子，寓意粮食满园、称心如意、十全十美，右图为一种婚庆升斗的规格，该升斗外形是一个正四棱台，上、下底边边长分别为 $20 c m$ ， $10 c m$ ，侧棱长为 $10 c m$ ，忽略其壁厚，则该升斗的容积为 $c m^{3}$ ．

查看试题解析
3. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 棱长为3，在正方体的顶点中，到平面 $A_{1} D B$ 的距离为 $\sqrt{3}$ 的顶点可能是.（写出一个顶点即可）

查看试题解析
4. 在正四棱台 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = 2 ， A_{1} B_{1} = 1 ， A A_{1} = \sqrt{2}$ ，则该棱台的体积为.

查看试题解析
5. 多面体 $E - A B C D$ 的各顶点在半径为2的球面上， $A B C D$ 是矩形， $A B = 3 ， A D = 2$ ，则多面体体积的最大值为.

查看试题解析
6. 半径为2的半圆卷成一个圆锥，则该圆锥的体积为

查看试题解析
7. 已知圆锥的底面半径为2，侧面展开图是一个圆心角为120°的扇形.把该圆锥截成圆台，已知圆台的下底面与该圆锥的底面重合，圆台的上底面半径为1，则圆台的体积为.

查看试题解析
8. 已知圆锥的轴截面是边长为 $2$ 的等边三角形，则圆锥的体积为．

查看试题解析
9. 已知圆台的下底面半径为6，上底面半径为3，其侧面积等于上、下底面积之和，则圆台的高为．

查看试题解析
10. 我国古代数学名著《九章算术》中将底面为矩形且有一侧棱垂直于底面的四棱锥称为“阳马”．现有一“阳马”（如图所示），其中 $P A ⊥$ 底面 $A B C D$ ， $P A = 3$ ， $A B = 2$ ， $A D = 1$ ，则该“阳马”的外接球的表面积为．

查看试题解析
11. 棱长都是3的三棱锥的高等于.

查看试题解析

三、提升

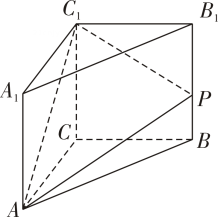
12. 如图，是由正四棱锥和长方体拼接而成的组合体，其顶点都在半径为 $R$ 的球面上，记 $r$ 为 $A B C D$ 的外接圆半径.若该正四棱锥和长方体体积相等，则 $\frac{r}{R} =$ .

查看试题解析
13. 在三棱锥 $P - Q R S$ 中， $P Q = R S = P R = Q S = \sqrt{15}$ ， $P S = Q R = 3 \sqrt{2}$ ，则三棱锥 $P - Q R S$ 外接球的体积与三棱锥 $P - Q R S$ 的体积之比为.

查看试题解析
14. 要做一个无盖的长方体箱子，其体积为 $36 m^{3}$ ，底面长方形长与宽的比为 $2 ： 1$ ，则当它的宽为 $m$ 时，可使其表面积最小，最小表面积为 $m^{2}$ .

查看试题解析
15. 在棱长为a的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，E，F分别为棱BC， $C C_{1}$ 的中点，过点A，E，F作一个截面，该截面将正方体分成两个多面体，则体积较小的多面体的体积为.

查看试题解析
16. 在三棱锥 $A - B C D$ 中， $△ B C D$ 是边长为6的等边三角形， $∠ B A D = \frac{π}{3}$ ，三棱锥 $A - B C D$ 体积的最大值是；当二面角 $A - B D - C$ 为 $12 0^{∘}$ 时，三棱锥 $A - B C D$ 外接球的表面积是.

查看试题解析
17. 正四面体ABCD的棱长为3，P在棱AB上，且满足 $\vec{B A} = 3 \vec{B P}$ ，记四面体ABCD的内切球为球 $O_{1}$ ，四面体PBCD的外接球为球 $O_{2}$ ，则 $| O_{1} O_{2} | =$ ．

查看试题解析
18. 在正四棱台 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = 3 \sqrt{2}$ ， $A_{1} B_{1} = 2 \sqrt{2}$ ， $A A_{1} = 2$ ， $A C ∩ B D = O$ ， $\vec{C E} = λ \vec{C C_{1}}$ ，若 $O E / /$ 平面 $A B_{1} D_{1}$ ，则 $λ =$ ．

查看试题解析
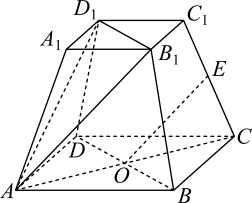19. 已知一个球与一个正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 的三个侧面和两个底面都相切，且这个球的体积为 $\frac{32}{3} π$ ，那么这个三棱柱的侧面积为，二面角 $A - B_{1} C_{1} - A_{1}$ 的正弦值为．

查看试题解析
20. 如图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为2，E，F分别为 $B_{1} C_{1}$ ， $C_{1} D_{1}$ 的中点，P是底面 $A_{1}^{} B_{1}^{} C_{1}^{} D_{1}^{}$ 上一点．若 $A P / /$ 平面BEF，则AP与平面 $A_{1}^{} B_{1}^{} C_{1}^{} D_{1}^{}$ 成角的正弦值的取值范围是．

查看试题解析
21. 如图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为2， $E$ 是棱 $A B$ 的中点， $F$ 是侧面 $A A_{1} D_{1} D$ 内一点，若 $E F / /$ 平面 $B B_{1} D_{1} D$ ，则 $E F$ 的长度的范围为.

查看试题解析
22. 在边长为2的菱形 $A B C D$ 中， $∠ A B C = \frac{π}{3}$ ，将菱形 $A B C D$ 沿对角线 $A C$ 翻折，取 $A C$ 的中点 $N$ ，连接 $B N ， D N$ ，若 $c o s ∠ B N D = \frac{1}{2}$ ，则三棱锥 $A - B C D$ 的外接球的半径为.

查看试题解析

四、培优

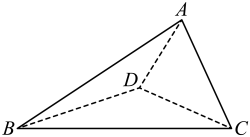
23. 如图1，在矩形ABCD中， $A B = 2 A D = 2$ ， E为AB的中点，将 $△ A D E$ 沿DE折起，点A折起后的位置记为点 $A_{1}$ ，得到四棱锥 $A_{1} - B C D E$ ， M为AC的中点，如图2.某同学在探究翻折过程中线面位置关系时，得到下列四个结论：

①恒有 $A_{1} D ⊥ A_{1} E$ ； ②恒有 $B M / /$ 平面 $A_{1} D E$ ；

③三棱锥 $A_{1} - D E M$ 的体积的最大值为 $\frac{\sqrt{2}}{12}$ ； ④存在某个位置，使得平面 $A_{1} D E ⊥$ 平面 $A_{1} C D$ .

其中所有正确结论的序号是.

查看试题解析
24. 已知直四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长均为2， $∠ B A D = 60 °$ ，除面ABCD外，该四棱柱其余各个面的中心分别为点E，F，G，H，Ⅰ，则由点E，F，G，H，Ⅰ构成的四棱锥的体积为．

查看试题解析
25. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为矩形， $A P ⊥$ 底面 $A B C D$ ， $E$ 为棱 $A B$ 上任意一点（不包括端点）， $F$ 为棱 $P D$ 上任意一点（不包括端点），且 $\frac{A E}{A B} = \frac{D F}{D P}$ ．已知 $A B = A P = 1$ ， $B C = 2$ ，当三棱锥 $C - B E F$ 的体积取得最大值时， $E F$ 与底面 $A B C D$ 所成角的正切值为．

查看试题解析
26. 正四棱柱ABCD﹣A₁B₁C₁D₁中，AB＝2，AA₁＝4，E为AB的中点，点F满足 $\vec{C_{1} F} = 3 \vec{F C}$ ，动点M在侧面AA₁D₁D内运动，且MB∥平面D₁EF ，则|MD|的取值范围是．

查看试题解析
27. 如图，已知两矩形 $A B C D$ 与 $A D E F$ 所在平面互相垂直， $A B = 1$ 是，若将 $Δ D E F$ 沿着直线 $F D$ 翻折，使得点 $E$ 落在边 $B C$ 上（即点 $P$ ），则当 $A D$ 取最小值时，边 $A F$ 的长是.

查看试题解析
28. 18世纪英国数学家辛卜森运用定积分，推导出了现在中学数学教材中柱、锥、球、台等几何体 $Ω$ 的统一体积公式 $V = \frac{1}{6} h (L + 4 M + N)$ （其中 $L$ ， $N$ ， $M$ ， $h$ 分别为 $Ω$ 的上底面面积、下底面面积、中截面面积和高），我们也称为“万能求积公式”.例如，已知球的半径为 $R$ ，可得该球的体积为 $V = \frac{1}{6} \times 2 R (0 + 4 \times π R^{2} + 0) = \frac{4}{3} π R^{3}$ ；已知正四棱锥的底面边长为 $a$ ，高为 $h$ ，可得该正四棱锥的体积为 $V = \frac{1}{6} \times h [0 + 4 \times {(\frac{a}{2})}^{2} + a^{2}] = \frac{1}{3} a^{2} h$ .类似地，运用该公式求解下列问题：如图，已知球 $O$ 的表面积为 $16 π c m^{2}$ ，若用距离球心 $O$ 都为1cm的两个平行平面去截球 $O$ ，则夹在这两个平行平面之间的几何体 $Π$ 的体积为 $c m^{3}$ .

查看试题解析
29. 如图，直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A C ⊥ B C ， A C = \sqrt{7}$ ， $B C = 3$ ，点 $P$ 在棱 $B B_{1}$ 上，且 $P A ⊥ P C_{1}$ ，当 $△ A P C_{1}$ 的面积取最小值时，三棱锥 $P - A B C$ 的外接球的表面积为.

查看试题解析
30. 如图，三棱锥 $A - B C D$ 中，平面 $A C D ⊥$ 平面BCD ， $△ A C D$ 是边长为2的等边三角形， $B D = C D$ ， $∠ B D C = 120 °$ .若A ， B ， C ， D四点在某个球面上，则该球体的表面积为.

查看试题解析