广东省广州市明珠教育集团2023-2024学年八年级上学期数学期中试题

试卷更新日期：2023-11-21 类型：期中考试

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选择项中，只有一项是符合题目要求的．

1. 下列交通标志中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 平面直角坐标系中，点P(2，1)关于x轴对称的点的坐标是（）

A、 $(2 ， 1)$ B、 $(2 ， - 1)$ C、 $(- 2 ， 1)$ D、 $(- 2 ， - 1)$

查看试题解析
3. 一个三角形的两边长分别为3cm和8cm，则此三角形第三边长可能是（）

A、3cm B、5cm C、7cm D、11cm

查看试题解析
4. 只用下列图形不能进行平面镶嵌的是（）

A、正六角形 B、正五边形 C、正四边形 D、正三边形

查看试题解析
5. 下列结论正确的是（）

A、有两个锐角相等的两个直角三角形全等； B、顶角和底边对应相等的两个等腰三角形全等 C、一条斜边对应相等的两个直角三角形全等； D、两个等边三角形全等.

查看试题解析
6. 已知一个多边形的每个内角都是144°，则这个多边形是（）

A、七边形 B、八边形 C、九边形 D、十边形

查看试题解析
7. 如图，在△ABC中，∠C＝90°，∠A＝30°，AB的垂直平分线分别交AB，AC于点D，E，则下列结论正确的是（）

A、AE＝3CE B、AE＝2CE C、AE＝BD D、BC＝2CE

查看试题解析
8. 如图，在 $△ A B C$ 中， $∠ B = 34 °$ ， $∠ C = 58 °$ ， AE是BC边上的高，AD是 $∠ B A C$ 的平分线，则 $∠ D A E$ 的度数为（）

A、8° B、10° C、12° D、14°

查看试题解析
9. 如图， $△ A B C$ 三边的中线 $A D$ ， $B E$ ， $C F$ 的公共点为G，且 $A G ： G D = 2 ： 1$ ．若 $△ A B C$ 的面积为12，则图中阴影部分的面积是（）

A、2 B、4 C、6 D、8

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ A B C = 50 °$ ， $A C$ 边上有一个定点P，M、N分别是 $A B$ 和 $B C$ 边上的动点，当 $△ P M N$ 的周长最小时， $∠ M P N$ 的度数是（）

A、 $50 °$ B、 $60 °$ C、 $80 °$ D、 $100 °$

查看试题解析

二、填空题：本大题共5小题，每小题3分，共15分．

11. 如图，在△ABC中，∠A＝30°，∠B＝50°，延长BC到点D，则∠ACD＝°.

查看试题解析
12. 如图， $△ A B C ≌ △ B D E$ ，若 $A B = 12$ ， $E D = 5$ ，则 $C D$ 的长为．

查看试题解析
13. 如图，△ABC≌△ADE，且E在BC上．若∠DEA＝80°，则∠BED的度数为．

查看试题解析
14. 如图，∠A+∠B+∠C+∠D+∠E= ．

查看试题解析
15. 如图，等边△ABC的边长为1cm，D、E分别是AB、AC上的点，将△ADE沿直线DE折叠，点A落在点A′处，且点A′在△ABC外部，则阴影部分图形的周长为cm．

查看试题解析

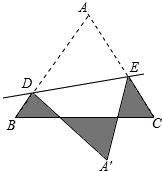
三、解答题（一）：本大题共3小题，每小题8分，共24分．

16. 如图，在四边形 $A B C D$ 中， $∠ A = ∠ C$ ， $∠ B = ∠ D$ ，求证： $A B ∥ C D$ ．

查看试题解析
17. 如图，点B、E、C、F在一条直线上，AB=DE，AC=DF，BE=CF．求证：∠A=∠D．

查看试题解析
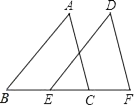18. 如图，在平面直角坐标系中，点A，B，C的坐标分别为 $(- 1 ， 2)$ ， $(- 3 ， 0)$ ， $(- 3 ， - 2)$ ．

(1)、画出 $△ A B C$ 关于y轴对称的 $△ A_{1} B_{1} C_{1}$ ，并分别写出点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标；

(2)、在y轴上找出点P，使 $P A + P C$ 的值最小．

查看试题解析

四、解答题（二）：本大题共3小题，每小题9分，共27分．

19. 如图，在 $△ A B C$ 中， $∠ A = 50 °$ ， $∠ C = 65 °$ ， $A B = 13$ ， $B C = 11$ ．

(1)、尺规作图：作 $A B$ 的垂直平分线 $D E$ ，交 $A B$ 于点D，交 $A C$ 于点E（不要求写作法，但要保留作图痕迹）；

(2)、在（1）的条件下，连接 $B E$ ，求 $∠ E B C$ 的度数和 $△ B C E$ 的周长．

查看试题解析
20. 如图， $△ A B C$ 中， $∠ A B C = 45 °$ ， P为 $B C$ 边上一点，且 $P C = 2 P B$ ， $∠ A P C = 60 °$ ，过点C作 $C D ⊥ A P$ ，垂足为D，连接 $B D$ ．

(1)、求证： $△ P B D$ 是等腰三角形；

(2)、求 $∠ A C B$ 的度数．

查看试题解析
21. 如图，在 $△ A B C$ 中， $A D$ 平分 $∠ B A C$ ．

(1)、求证： $S_{△ A B D} ： S_{△ A C D} = A B ： A C$ ；

(2)、若 $A B = 8$ ， $A C = 6$ ， $B C = 7$ ，求 $B D$ 的长．

查看试题解析

五、解答题（三）：本大题共2小题，每小题12分，共24分．

22. 如图，在 $△ A B C$ 中， $B C$ 边的垂直平分线 $D E$ 与 $∠ B A C$ 的平分线交于点E， $E F ⊥ A B$ 交 $A B$ 的延长线于点F， $E G ⊥ A C$ 交 $A C$ 于点G．

(1)、求证： $B F = C G$ ；

(2)、若 $A B = a$ ， $A C = b (a < b)$ ，且 $a + b = 14$ ，试问线段AF的长度是否为定值？如果是，请求出这个定值；如果不是，请说明理由．

查看试题解析
23.
如图1，在 $△ A B C$ 中， $∠ B A C \neq 120 °$ ，分别以 $A B 、 A C$ 为边向外作两个等边三角形 $△ A B D$ 和 $△ A C E$ ，连接 $B E 、 D C$ ， $B E$ 与 $D C$ 交于点M，连接 $A M$ ．

(1)、求证： $B E = D C$ ；

(2)、求证： $M A$ 平分 $∠ D M E$ ；

(3)、如图2，G、F分别是 $D C$ 与 $B E$ 的中点，连接 $A F 、 F G ，$ 试问 $∠ A F G$ 是否为定值，如果是，请求出它的度数，如果不是，请说明理由．

查看试题解析