广东省广州市增城区2023-2024学年七年级上学期数学期中试题

试卷更新日期：2023-11-21 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，满分30分．在每小题给出的四个选项中，只有一项是符合题目要求的．）

1. 我国古代数学著作《九章算术》中首次正式引入负数，如果支出200元记作 $- 200$ 元，那么收入60元记作（）．

A、 $+ 60$ 元 B、 $- 60$ 元 C、140元 D、 $- 140$ 元

查看试题解析
2. $- 5$ 的倒数是（）．

A、5 B、 $- 5$ C、 $\frac{1}{5}$ D、 $- \frac{1}{5}$

查看试题解析
3. 2023年“五一”假期，文化和旅游行业复苏势头强劲，全国假日市场平稳有序，经文化和旅游部数据中心测算，全国国内旅游出游合计2.74亿人次，同比增长 $70.83 %$ ．其中“2.74亿”用科学记数法表示为（）．

A、 $27.4 \times 1 0^{8}$ B、 $2.74 \times 1 0^{8}$ C、 $0.274 \times 1 0^{9}$ D、 $2.74 \times 1 0^{9}$

查看试题解析
4. 单项式 $- 2^{3} a b^{4}$ 的次数与系数分别是（）．

A、 $5 ， - 2$ B、 $4 ， - 8$ C、 $5 ， - 8$ D、5，8

查看试题解析
5. 一个两位数的十位数字为 $a$ ，个位数字为 $b$ ，那么这个两位数可以表示为（）．

A、 $10 a b$ B、 $10 a + b$ C、 $10 b + a$ D、 $a b$

查看试题解析
6. 下列计算正确的是（）．

A、 $4 a^{2} b - 3 b a^{2} = a^{2} b$ B、 $5 a^{3} - 3 a^{2} = 2 a$ C、 $5 a + 2 b = 7 a b$ D、 $- \frac{1}{2} y^{2} - \frac{1}{4} y^{2} = - \frac{3}{4} y^{4}$

查看试题解析
7. 下列去括号正确的是（）．

A、 $- 3 (x - 1) = - 3 x + 1$ B、 $- (a - b + c) = - a + b + c$ C、 $- (x - 6) = 6 - x$ D、 $- [x - (y - z)] = - x - y + z$

查看试题解析
8. 若多项式 $a^{2} + 2 a + 3$ 的值为8．则多项式 $2 a^{2} + 4 a + 10$ 的值为（）．

A、20 B、32 C、0 D、12

查看试题解析
9. 在 $45 % ， - (- 5) ， | - \frac{1}{3} | ， 30 ， 0 ， - 2^{2} ， - | - 2 |$ 这七个数中，正数的个数是（）．

A、3个 B、4个 C、5个 D、6个

查看试题解析
10. 现定义运算：对于任意有理数 $a 、 b$ ，都有 $a \otimes b = a^{2} - 3 b$ ，如： $1 \otimes 3 = 1^{2} - 3 \times 3 = - 8$ ，则 $- 5 \otimes (- 2 \otimes 3)$ 的值为（）．

A、20 B、25 C、38 D、40

查看试题解析

二、填空题（本大题共6小题，每小题3分，满分18分．）

11. 计算： $5 + (- 3) =$ .

查看试题解析
12. 比较大小： $- \frac{2}{3}$ $- \frac{3}{4}$ ．

查看试题解析
13. 用四舍五入法对1.804取近似数，并精确到0.01，得到的值是．

查看试题解析
14. 若 $| x | = 6$ ，则 $x =$ ．

查看试题解析
15. 已知 $a 、 b$ 互为相反数，且 $a \neq 0 ， c 、 d$ 互为倒数， $m$ 是最小的正整数，则 $m + 3 (a + b) - 2 c d$ 的值．

查看试题解析
16. 数轴上有一动点 $A$ ，从原点出发沿着数轴移动，第一次点 $A$ 向左移动1个单位长度到达点 $A_{1}$ ，第二次将点 $A_{1}$ 向右移动2个单位长度到达点 $A_{2}$ ，第三次将点 $A_{2}$ 向左移动3个单位长度到达点 $A_{3}$ ，按照这种移动规律移动下去，第 $n$ 次移动到点 $A_{n}$ ，当 $n = 2023$ 时，点 $A$ 与原点的距离是个单位．

查看试题解析

三、解答题（本大题共9小题，满分72分．解答应写出文字说明、证明过程或演算步骤．）

17. 计算： $(- 20) + (+ 3) - (- 5) - (+ 7)$ ．

查看试题解析
18. 计算： $(4 x^{2} y - 5 x y^{2}) - 3 (x^{2} y - 4 x y^{2})$ ．

查看试题解析
19. 计算： $2 \times {(- 3)}^{2} + 4 \times (- 3) + (- 15) \div 5 - {(- 1)}^{7}$ ．

查看试题解析
20. 先化简下式，再求值：
$(3 a^{3} - 2 a b + b^{2}) - 2 (- a^{3} - a b + 5 b^{2})$ ，其中 $a = - 2 ， b = \frac{1}{3}$ ．

查看试题解析
21. 有20筐白菜，以每筐 $25 k g$ 为标准，超过的千克数记作正数，不足的千克数记作负数，称后的记录如下：
与标准质量的差值（单位： $k g$ ）
$- 3$
$- 2$
$- 1.5$
0
1
2.5
筐数
1
4
2
3
2
8
若白菜每千克售价2.5元，则出售这20筐白菜可卖多少元？

查看试题解析
22. 某同学绘制了如图所示的火箭模型截面图，图的下面是梯形，中间是长方形，上面是三角形．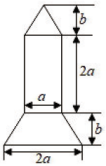

(1)、用含有 $a 、 b$ 的代数式表示该截面的面积 $S$ ；

(2)、当 $a = 2.8 c m ， b = 2.2 c m$ 时，求这个截面的面积．

查看试题解析
23. 两船从同一港口同时出发反向而行，甲船顺水，乙船逆水，两船在静水中的速度都是60 $k m / h$ ，水流速度是 $a k m / h$ ，则 $3 h$ 后甲船比乙船多航行多少千米？

查看试题解析
24. 某市出租车的计价标准为：行驶路程不超过3千米收费10元，超过3千米的部分按每千米2.4元收费．

(1)、若某人乘坐2千米，则应支付车费元，若乘坐8千米，则应支付车费元，若乘坐了 $x (x > 3)$ 千米，则应支付车费元（用含有 $x$ 的代数式表示）；

(2)、一出租车公司坐落于东西向的大道边，驾驶员李师傅从公司出发，在此大道上连续接送4批客人，行驶路程记录如下（规定向东为正，向西为负，单位：千米）
第1批
第2批
第3批
第4批
$+ 1.6$
$- 9$
$+ 2.9$
$- 7$
①送完第4批客人后，李师傅在公司的什么方向？距离公司多少千米？
②若李师傅的车平均每千米耗油0.1升，则送完第4批客人后，李师傅用了多少升油？

查看试题解析
25. 如图，若点 $A$ 在数轴上对应的数为 $a$ ，点 $B$ 在数轴上对应的数为 $b$ ，且 $a ， b$ 满足 $| a - 1 | + {(b + 2)}^{2} = 0$ ．

(1)、求线段 $A B$ 的长．

(2)、点 $C$ 在数轴上对应的数是 $c$ ，且 $c$ 是方程 $4 x - 6 = x$ 的解，在数轴上是否存在点 $P$ ，使得 $P A + P B = P C$ ？若存在，求出点 $P$ 对应的数；若不存在，请说明理由．

(3)、在（1）、（2）的条件下，点 $A 、 B 、 C$ 开始在数轴上运动，若点 $B$ 以每秒1个单位长度的速度向左运动，同时点 $A$ 和点 $C$ 分别以每秒4个单位长度和9个单位长度的速度向右运动， $t$ 秒钟后，若点 $A$ 和点 $C$ 之间的距离表示为 $A C$ ，点 $A$ 和点 $B$ 之间的距离表示为 $A B$ ，那么 $A B - A C$ 的值是否随着时间 $t$ 的变化而变化？若变化，请说明理由；若不变，请求出 $A B - A C$ 的值．

查看试题解析

与标准质量的差值（单位： $k g$ ）	$- 3$	$- 2$	$- 1.5$	0	1	2.5
筐数	1	4	2	3	2	8

第1批	第2批	第3批	第4批
$+ 1.6$	$- 9$	$+ 2.9$	$- 7$