陕西省西安市2023-2024学年八年级上学期数学期中试题

试卷更新日期：2023-11-21 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 下列关系式中，y不是x的函数的是（）

A、 $y = \frac{x}{2}$ B、 $y = 2 x^{2}$ C、 $y = \sqrt{x} (x \geq 0)$ D、 $| y | = x$

查看试题解析
2. 下列方程组中，二元一次方程组有（）
① ${\begin{array}{l} 4 x + y = 2 \\ x - 2 y = - 3 \end{array}$ ；② ${\begin{array}{l} 2 x - y = 1 \\ y + z = 1 \end{array}$ ；③ ${\begin{array}{l} x = 3 \\ y - 5 = 0 \end{array}$ ；④ ${\begin{array}{l} x - 2 y^{2} = 3 \\ x + 3 y = 1 \end{array}$ ．

A、4个 B、3个 C、2个 D、1个

查看试题解析
3. 关于函数 $y = 2 x - 4$ 的图像，下列结论正确的是（）

A、必经过点(1，2) B、与x轴交点的坐标为(0，-4) C、过第一、三、四象限 D、可由函数 $y = - 2 x$ 的图像平移得到

查看试题解析
4. 根据如图所示的程序计算函数y的值，若输入x的值是7，则输出y的值是﹣2，若输入x的值是﹣8，则输出y的值是（）

A、5 B、10 C、19 D、21

查看试题解析
5. 已知函数y=3x+1，当自变量x增加m时，相应函数值增加（）

A、3m+1 B、3m C、m D、3m-1

查看试题解析
6. 已知直线 $y = - \frac{1}{2} x + 1$ 与直线l关于x轴对称，则直线l与y轴的交点坐标是（）

A、 $(0 ， - 1)$ B、 $(0 ， 1)$ C、 $(2 ， 0)$ D、 $(- 2 ， 0)$

查看试题解析
7. 如图，一次函数y＝kx+b与y＝x+2的图象相交于点P（m，4），则关于x的方程kx+b＝4的解是（）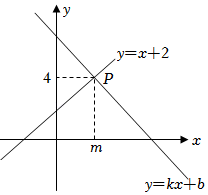

A、x＝1 B、x＝2 C、x＝3 D、x＝4

查看试题解析
8. 已知等腰三角形的两边长分别为a、b，且a、b满足 $\sqrt{2 a - 3 b + 5} + (3 a - 2 b - 10)^{2} = 0$ ，则此等腰三角形的周长为（）

A、22或21 B、22或23 C、23或24 D、22或24

查看试题解析
9. 两条直线 $y = a x - b$ 与 $y = b x - a$ ，在同一平面直角坐标系中的图象可能是图中的（）

A、 B、 C、 D、

查看试题解析
10. 如图，在平面直角坐标系中，函数 $y = x$ 和 $y = - \frac{1}{2} x$ 的图象分别为直线 $l_{1} 、 l_{2}$ ，过点 $A_{1} (1 ， - \frac{1}{2})$ 作x轴的垂线交 $l_{1}$ 于点 $A_{2}$ ，过点 $A_{2}$ 作y轴的垂线交 $l_{2}$ 于点 $A_{3}$ ，过点 $A_{3}$ 作x轴的垂线交 $l_{1}$ 于点 $A_{4}$ ，过点 $A_{4}$ 作y轴的垂线交 $l_{2}$ 于点 $A_{5}$ ……依次进行下去，则点 $A_{2023}$ 的横坐标为（）

A、 $2^{1012}$ B、 $- 2^{1012}$ C、 $- 2^{1011}$ D、 $2^{1011}$

查看试题解析

二、填空题（每小题3分，共21分）

11. 函数 $y = \sqrt{x + 1}$ 的自变量x的取值范围为．

查看试题解析
12. 一次函数的图象过点 $(0 ， - 1)$ ，且函数值随着自变量的增大而减小，写出一个符合这个条件的一次函数解析式：．

查看试题解析
13. 已知 $y = (m + 2) x^{| m + 3 |} + n - 2$ ， y是x的正比例函数，则 $m =$ ， $n =$ ．

查看试题解析
14. 甲、乙两人都解方程组 ${\begin{array}{l} a x + y = 2 \\ 2 x - b y = 1 \end{array}$ ，甲看错a解得 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ ，乙看错b解得 ${\begin{array}{l} x = 1 \\ y = 1 \end{array}$ ，则方程组正确的解是．

查看试题解析
15. 直线 $y = k x + b$ 的图象经过点 $A (0 ， 1) ， B (3 ， 0)$ ，若将该图象沿着x轴向左平移2个单位长度，得到的直线表达式为．

查看试题解析
16. 已知两直线 $y = 4 x - 2 ， y = 3 m - x$ 的交点在第三象限，则m的取值范围为．

查看试题解析
17. 对于平面直角坐标系中的点P（x，y），若x，y满足|x-y|＝5，则点P（x，y）就称为“平衡点”．例如：（1，6），因为|1-6|＝5，所以（1，6）是“平衡点”．已知一次函数y＝3x+k（k为常数）图象上有一个“平衡点”的坐标是（3，8），则一次函数y＝3x+k（k为常数）图象上另一“平衡点”的坐标是．

查看试题解析

三、解答题（共49分）

18. 解方程组：

(1)、 ${\begin{array}{l} y = 4 x \\ 3 x + y = 14 \end{array}$ ；

(2)、 ${\begin{array}{l} 3 x + 2 y = 3 \\ x + 3 y = 8 \end{array}$ ；

(3)、 ${\begin{array}{l} x - 2 y = 0 \\ 3 x + 2 y = 16 \end{array}$ ；

(4)、 ${\begin{array}{l} 3 x + 5 y = 19 \\ 8 x - 3 y = 67 \end{array}$ ．

查看试题解析
19. 若关于 $x 、 y$ 的二元一次方程组 ${\begin{array}{l} a x + b y = 5 \\ y = 2 x - 1 \end{array}$ 和 ${\begin{array}{l} a x - b y = 1 \\ x + y = 2 \end{array}$ 的解相同，求 $a 、 b$ 的值.

查看试题解析
20. 《孙子算经》中记载：“今有三人共车，二车空二人共车，九人步，问人与车各何？”译文大意为：令有若干人乘车，每三人乘一辆车，最终剩余2辆车；若每2人共乘一辆车，最终剩余9个人无车可乘，问有多少人，多少辆车？
请解答上述问题．

查看试题解析
21. 如图，直线 $l_{1} ： y = 2 x + 1$ 与直线 $l_{2} ： y = m x + 4$ 相交于点 $P (1 ， b)$ ．

(1)、求b，m的值；

(2)、垂直于x轴的直线交直线 $l_{1} ， l_{2}$ 于C，D两点，若线段CD长为6，求点D的坐标．

查看试题解析
22. 一个有进水管与出水管的容器，从某时刻开始4分钟内只进水不出水，在随后的8分钟内既进水又出水，12分钟后关闭进水管，放空容器中的水，每分钟的进水量和出水量是两个常数。容器内水量y (单位：升)与时间x (单位：分钟)之间的关系如图所示。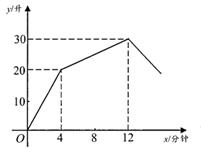

(1)、每分钟进水多少升？

(2)、当4<x≤12时，求y关于x的函数解析式；

(3)、容器中储水量不低于15 升的时长是多少分钟？

查看试题解析
23. 在平面直角坐标系xOy中，点A、B分别在y轴和x轴上，已知点A（0，4）．以AB为直角边在AB左侧作等腰直角△ABC，∠CAB＝90°．

(1)、当点B在x轴正半轴上，且AB＝8时
①求AB解析式；
②求C点坐标；

(2)、当点B在x轴上运动时，连接OC，求AC+OC的最小值及此时B点坐标．

查看试题解析