【北师大版·数学】2024年中考一轮复习之解直角三角形的应用-仰角俯角问题
试卷更新日期:2023-11-20 类型:一轮复习
一、选择题
-
1. 如图,从热气球A看一栋楼底部C的俯角是( )
 A、 B、 C、 D、2. 如图,在教室前面墙壁 A 处安装了一个摄像头,当恰好观测到后面墙壁与底面交接处点 C 时,摄像头俯角约为 17°,受安装支架限制,摄像头观测的俯角最大约为 54° ,已知教室的长 (教室前后墙壁之间的距离 BC 的值) 是 9米,若摄像头与安装的墙壁之间距离忽略不计,则摄像头安装点高度 AB 约为( )米.(sin17° ≈ 0.29,tan17° ≈ 0.30,sin54° ≈ 0.8 ,tan54° ≈ 1.33,精确到 0.1 米) .
A、 B、 C、 D、2. 如图,在教室前面墙壁 A 处安装了一个摄像头,当恰好观测到后面墙壁与底面交接处点 C 时,摄像头俯角约为 17°,受安装支架限制,摄像头观测的俯角最大约为 54° ,已知教室的长 (教室前后墙壁之间的距离 BC 的值) 是 9米,若摄像头与安装的墙壁之间距离忽略不计,则摄像头安装点高度 AB 约为( )米.(sin17° ≈ 0.29,tan17° ≈ 0.30,sin54° ≈ 0.8 ,tan54° ≈ 1.33,精确到 0.1 米) . A、2 B、2.7 C、3 D、3.23. 某中学九年级数学兴趣小组的同学准备测量校内旗杆的高度,他们在点测得旗杆顶端的仰角 , 向前走了30米到达点,在点测得旗杆顶端A的仰角 , 则旗杆的高为多少米?( )
A、2 B、2.7 C、3 D、3.23. 某中学九年级数学兴趣小组的同学准备测量校内旗杆的高度,他们在点测得旗杆顶端的仰角 , 向前走了30米到达点,在点测得旗杆顶端A的仰角 , 则旗杆的高为多少米?( ) A、15米 B、米 C、米 D、米4. 如图,某地修建高速公路,要从A地向B地修一条隧道(点A,B在同一水平面上).为了测量A,B两地之间的距离,一架直升飞机从A地出发,垂直上升600米到达C处,在C处观察B地的俯角为α,则A,B两地之间的距离为( )
A、15米 B、米 C、米 D、米4. 如图,某地修建高速公路,要从A地向B地修一条隧道(点A,B在同一水平面上).为了测量A,B两地之间的距离,一架直升飞机从A地出发,垂直上升600米到达C处,在C处观察B地的俯角为α,则A,B两地之间的距离为( ) A、600sinα米 B、600tanα米 C、米 D、米5. 小致利用测角仪和皮尺测量学校旗杆的高度,如图,小致在 处测得顶端 的仰角∠ = , 到旗杆的距离 =5米,测角仪 的高度为1米,则旗杆 的高度表示为( ).
A、600sinα米 B、600tanα米 C、米 D、米5. 小致利用测角仪和皮尺测量学校旗杆的高度,如图,小致在 处测得顶端 的仰角∠ = , 到旗杆的距离 =5米,测角仪 的高度为1米,则旗杆 的高度表示为( ).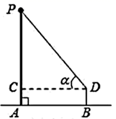 A、5 +1 B、5 +1 C、5 +1 D、 +16. 如图,从航拍无人机看一栋楼顶部的仰角为 , 看这栋楼底部的俯角为 , 无人机与楼的水平距离为 , 则这栋楼的高度为( )
A、5 +1 B、5 +1 C、5 +1 D、 +16. 如图,从航拍无人机看一栋楼顶部的仰角为 , 看这栋楼底部的俯角为 , 无人机与楼的水平距离为 , 则这栋楼的高度为( ) A、 B、 C、 D、7. 日照灯塔是日照海滨港口城市的标志性建筑之一,主要为日照近海及进出日照港的船舶提供导航服务.数学小组的同学要测量灯塔的高度,如图所示,在点B处测得灯塔最高点A的仰角 , 再沿方向前进至C处测得最高点A的仰角 , , 则灯塔的高度大约是( )(结果精确到 , 参考数据: , )
A、 B、 C、 D、7. 日照灯塔是日照海滨港口城市的标志性建筑之一,主要为日照近海及进出日照港的船舶提供导航服务.数学小组的同学要测量灯塔的高度,如图所示,在点B处测得灯塔最高点A的仰角 , 再沿方向前进至C处测得最高点A的仰角 , , 则灯塔的高度大约是( )(结果精确到 , 参考数据: , ) A、 B、 C、 D、8. “儿童放学归来早,忙趁东风放纸鸢”,小明周末在龙潭公园草坪上放风筝,已知风筝拉线长100米且拉线与地面夹角为(如图所示,假设拉线是直的,小明身高忽略不计),则风筝离地面的高度可以表示为( )
A、 B、 C、 D、8. “儿童放学归来早,忙趁东风放纸鸢”,小明周末在龙潭公园草坪上放风筝,已知风筝拉线长100米且拉线与地面夹角为(如图所示,假设拉线是直的,小明身高忽略不计),则风筝离地面的高度可以表示为( ) A、 B、 C、 D、9. 如图2,在两建筑物之间有一旗杆,高15米,从点A经过旗杆顶点恰好可观测到矮建筑物的最底端点C处,从点A测得点C的俯角α为60°,测得点D的俯角β为30°,若旗杆底部G为BC的中点,则,矮建筑物的高CD为( )
A、 B、 C、 D、9. 如图2,在两建筑物之间有一旗杆,高15米,从点A经过旗杆顶点恰好可观测到矮建筑物的最底端点C处,从点A测得点C的俯角α为60°,测得点D的俯角β为30°,若旗杆底部G为BC的中点,则,矮建筑物的高CD为( ) A、18米 B、20米 C、10米 D、(45-15)米10. 如图,某数学活动小组要测量校园内旗杆的高度,点B、C在同一条水平线上,测角仪在D处测得旗杆最高点A的仰角为 . 若测角仪 , , 则旗杆的高度为( )
A、18米 B、20米 C、10米 D、(45-15)米10. 如图,某数学活动小组要测量校园内旗杆的高度,点B、C在同一条水平线上,测角仪在D处测得旗杆最高点A的仰角为 . 若测角仪 , , 则旗杆的高度为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,某飞机在离地面垂直距离米的上空处,测得地面控制点的俯角为 , 那么飞机与该地面控制点之间的距离等于 米结果保留根号 .
 12. 如图,某飞机于空中处探测到某地面目标在点处,此时飞行高度米,从飞机上看到点的俯角为 , 飞机保持飞行高度不变,且与地面目标分别在两条平行直线上同向运动当飞机飞行米到达点时,地面目标此时运动到点处,从点看到点的仰角为 , 则地面目标运动的距离约为米参考数据: ,
12. 如图,某飞机于空中处探测到某地面目标在点处,此时飞行高度米,从飞机上看到点的俯角为 , 飞机保持飞行高度不变,且与地面目标分别在两条平行直线上同向运动当飞机飞行米到达点时,地面目标此时运动到点处,从点看到点的仰角为 , 则地面目标运动的距离约为米参考数据: , 13. 在一次综合实践活动中,某学校数学兴趣小组对一电视发射塔的高度进行了测量.如图,在塔前C处,测得该塔顶端B的仰角为 , 后退()到D处有一平台,在高()的平台上的E处,测得B的仰角为 . 则该电视发射塔的高度为 . (精确到 . 参考数据:)
13. 在一次综合实践活动中,某学校数学兴趣小组对一电视发射塔的高度进行了测量.如图,在塔前C处,测得该塔顶端B的仰角为 , 后退()到D处有一平台,在高()的平台上的E处,测得B的仰角为 . 则该电视发射塔的高度为 . (精确到 . 参考数据:) 14. 综合实践课上,航模小组用航拍无人机进行测高实践.如图,无人机从地面的中点A处竖直上升30米到达B处,测得博雅楼顶部E的俯角为 , 尚美楼顶部F的俯角为 , 已知博雅楼高度为15米,则尚美楼高度为米.(结果保留根号)
14. 综合实践课上,航模小组用航拍无人机进行测高实践.如图,无人机从地面的中点A处竖直上升30米到达B处,测得博雅楼顶部E的俯角为 , 尚美楼顶部F的俯角为 , 已知博雅楼高度为15米,则尚美楼高度为米.(结果保留根号) 15. 如图,无人机在空中A处测得某校旗杆顶部B的仰角为30o , 底部C的俯角为60o , 无人机与旗杆的水平距离AD为6m,则该校的旗杆高约为m.( , 结果精确到0.1)
15. 如图,无人机在空中A处测得某校旗杆顶部B的仰角为30o , 底部C的俯角为60o , 无人机与旗杆的水平距离AD为6m,则该校的旗杆高约为m.( , 结果精确到0.1)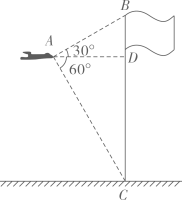
三、解答题
-
16. 如图,在一个坡度或坡比:的山坡上发现有一棵古树测得古树底端到山脚点的距离米,在距山脚点水平距离米的点处,测得古树顶端的仰角古树与山坡的截面、点在同一平面上,古树与直线垂直 , 求古树的高度参考数据: , ,
 17. 某校学生开展综合实践活动,测量某小区公园内路灯的高度如图,已知观测点 , 与路灯底端位于同一直线的水平线上,在点处测得路灯顶端的仰角为 , 在点处测得路灯顶端的仰角为 , 两个观测点 , 相距 , 求路灯的高度结果精确到 .
17. 某校学生开展综合实践活动,测量某小区公园内路灯的高度如图,已知观测点 , 与路灯底端位于同一直线的水平线上,在点处测得路灯顶端的仰角为 , 在点处测得路灯顶端的仰角为 , 两个观测点 , 相距 , 求路灯的高度结果精确到 . 参考数据: , 18. 某校数学社团开展“探索生活中的数学”研学活动,准备测量一栋大楼的高度.如图所示,其中观景平台斜坡的长是米,坡角为 , 斜坡底部与大楼底端的距离为米,与地面垂直的路灯的高度是米,从楼顶测得路灯顶端处的俯角是试求大楼的高度.
参考数据: , 18. 某校数学社团开展“探索生活中的数学”研学活动,准备测量一栋大楼的高度.如图所示,其中观景平台斜坡的长是米,坡角为 , 斜坡底部与大楼底端的距离为米,与地面垂直的路灯的高度是米,从楼顶测得路灯顶端处的俯角是试求大楼的高度.
参考数据: , , , , ,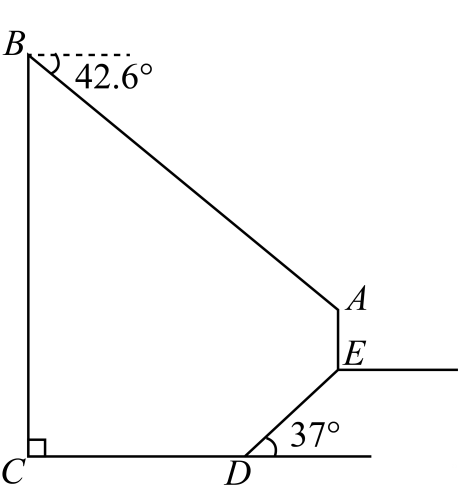
四、综合题
-
19. 如图1所示是一种太阳能路灯,它由灯杆和灯管支架两部分构成如图2,是灯杆,是灯管支架,灯管支架与灯杆间的夹角.综合实践小组的同学想知道灯管支架的长度,他们在地面的点E处测得灯管支架底部D的仰角为60°,在点F处测得灯管支架顶部C的仰角为30°,测得m,m(A,E,F在同一条直线上).根据以上数据,解答下列问题:
 (1)、求灯管支架底部距地面高度的长(结果保留根号);(2)、求灯管支架的长度(结果精确到0.1m,参考数据:).20. 小亮利用所学的知识对大厦的高度进行测量,他在自家楼顶B处测得大厦底部的俯角是 , 测得大厦顶部的仰角是 , 已知他家楼顶B处距地面的高度为40米(图中点A , B , C , D均在同一平面内).
(1)、求灯管支架底部距地面高度的长(结果保留根号);(2)、求灯管支架的长度(结果精确到0.1m,参考数据:).20. 小亮利用所学的知识对大厦的高度进行测量,他在自家楼顶B处测得大厦底部的俯角是 , 测得大厦顶部的仰角是 , 已知他家楼顶B处距地面的高度为40米(图中点A , B , C , D均在同一平面内).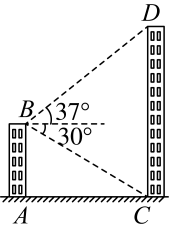 (1)、求两楼之间的距离(结果保留根号);(2)、求大厦的高度(结果取整数).
(1)、求两楼之间的距离(结果保留根号);(2)、求大厦的高度(结果取整数).(参考数据: , , , )
21. 年月日点分,“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射,成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站.如图,在发射的过程中,飞船从地面处发射,当飞船到达点时,从位于地面处的雷达站测得的距离是 , 仰角为;后飞船到达处,此时测得仰角为 .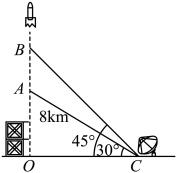 (1)、求点离地面的高度;(2)、求飞船从处到处的平均速度.(结果精确到 , 参考数据:)
(1)、求点离地面的高度;(2)、求飞船从处到处的平均速度.(结果精确到 , 参考数据:)