【北师大版·数学】2024年中考一轮复习之矩形的判定与性质
试卷更新日期:2023-11-20 类型:一轮复习
一、选择题
-
1. 下列说法错误的是( )A、矩形的对角线相等 B、正方形的对称轴有四条 C、平行四边形既是中心对称图形又是轴对称图形 D、菱形的对角线互相垂直且平分2. 下列说法中正确的是( )A、有两个角为直角的四边形是矩形 B、矩形的对角线互相垂直 C、平行四边形的对角线互相平分 D、对角线互相垂直的四边形是菱形3. 如图,直线、与双曲线分别相交于点 . 若四边形的面积为4,则的值是( )
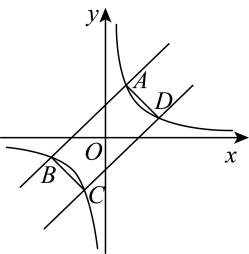 A、 B、 C、 D、14. 如图,在平面直角坐标中,矩形的边 , 将矩形沿直线折叠到如图所示的位置,线段恰好经过点 , 点落在轴的点位置,点的坐标是( )
A、 B、 C、 D、14. 如图,在平面直角坐标中,矩形的边 , 将矩形沿直线折叠到如图所示的位置,线段恰好经过点 , 点落在轴的点位置,点的坐标是( ) A、 B、 C、 D、5. 如图,在中, , 点P为线段上的动点,以每秒1个单位长度的速度从点A向点B移动,到达点B时停止.过点P作于点M、作于点N,连接 , 线段的长度y与点P的运动时间t(秒)的函数关系如图所示,则函数图象最低点E的坐标为( )
A、 B、 C、 D、5. 如图,在中, , 点P为线段上的动点,以每秒1个单位长度的速度从点A向点B移动,到达点B时停止.过点P作于点M、作于点N,连接 , 线段的长度y与点P的运动时间t(秒)的函数关系如图所示,则函数图象最低点E的坐标为( ) A、 B、 C、 D、6. 如图,以钝角三角形ABC最长边BC为边向外作矩形 , 连结 , 设 , , 的面积分别为 , 若要求出的值,只需知道( )
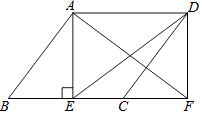
A、 B、 C、 D、6. 如图,以钝角三角形ABC最长边BC为边向外作矩形 , 连结 , 设 , , 的面积分别为 , 若要求出的值,只需知道( ) A、的面积 B、的面积 C、的面积 D、矩形的面积7. 如图, , 为矩形内两点, , 垂直 , 垂足分别为、 , 若 , , , 则( )
A、的面积 B、的面积 C、的面积 D、矩形的面积7. 如图, , 为矩形内两点, , 垂直 , 垂足分别为、 , 若 , , , 则( )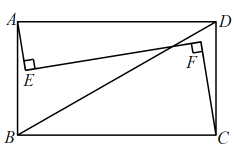 A、 B、5 C、 D、68. 如图,正六边形 , P点在上,记图中的面积为 , 已知正六边形边长,下列式子中不能确定的式子的是( )
A、 B、5 C、 D、68. 如图,正六边形 , P点在上,记图中的面积为 , 已知正六边形边长,下列式子中不能确定的式子的是( )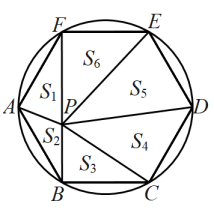 A、 B、 C、 D、9. 如图,矩形的对角线相交于点O, , 分别过点D,点C作的平行线,两线相交于点E,连接交于点F,则的值是( )
A、 B、 C、 D、9. 如图,矩形的对角线相交于点O, , 分别过点D,点C作的平行线,两线相交于点E,连接交于点F,则的值是( )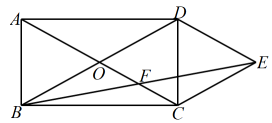 A、7 B、 C、8 D、10. 我们知道订书针的两条短边垂直长边.如图是由三枚完全相同的订书针ABCD,EFGH,IJKL拼成的图形,点B,E,C,F在同一条直线上,点D,K,L分别在JK,GF,HG上, 4B=CD=EF=GH=IJ=LK=1, BC=FG=JK=2.当点4, I重合时, HL的长度为( )
A、7 B、 C、8 D、10. 我们知道订书针的两条短边垂直长边.如图是由三枚完全相同的订书针ABCD,EFGH,IJKL拼成的图形,点B,E,C,F在同一条直线上,点D,K,L分别在JK,GF,HG上, 4B=CD=EF=GH=IJ=LK=1, BC=FG=JK=2.当点4, I重合时, HL的长度为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
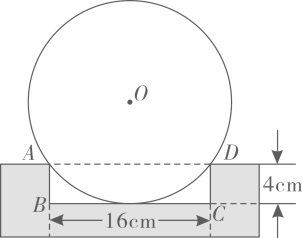
11. 如图是一个圆形餐盘的正面及其固定支架的截面图,凹槽ABCD是矩形.当䝳盘正立且紧靠支架于点A,D时,恰好与BC边相切,则此餐盘的半径等于.
 12. 如图,点A,B在轴上,分别以OA,AB为边,在轴上方作正方形OACD,ABEF.反比例函数的图象分别交边CD,BE于点P,Q.作轴于点轴于点.若为BE的中点,且阴影部分面积等于6,则的值为.
12. 如图,点A,B在轴上,分别以OA,AB为边,在轴上方作正方形OACD,ABEF.反比例函数的图象分别交边CD,BE于点P,Q.作轴于点轴于点.若为BE的中点,且阴影部分面积等于6,则的值为.
 13. 如图,将的按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,与尺下沿重合,与尺上沿的交点B在尺上的读数恰为 , 若按相同的方式将的放置在该刻度尺上,则与尺上沿的交点C在尺上的读数为 .
13. 如图,将的按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,与尺下沿重合,与尺上沿的交点B在尺上的读数恰为 , 若按相同的方式将的放置在该刻度尺上,则与尺上沿的交点C在尺上的读数为 .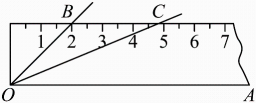 14. 如图,已知是反比例函数图象上的一点,过点作轴交的图象于点以 , 为边作▱ , 连结交轴于点 , 则 .
14. 如图,已知是反比例函数图象上的一点,过点作轴交的图象于点以 , 为边作▱ , 连结交轴于点 , 则 .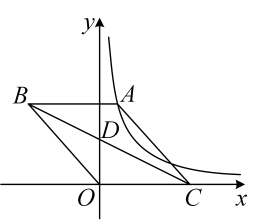 15. 如图,将的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2cm,若按相同的方式将的∠AOC放置在该尺上,则OC与尺上沿的交点C在尺上的读数约为cm
15. 如图,将的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2cm,若按相同的方式将的∠AOC放置在该尺上,则OC与尺上沿的交点C在尺上的读数约为cm(结果精确到0.1cm,参考数据: , , )

三、作图题
-
16. 已知:如图 , 线段 , .
求作:矩形 , 使得 , .
作法:如图 .
在直线上截取 .
过点作直线 , 在直线上截取 .
分别以点和点为圆心, , 的长为半径画弧,两弧的交点为 .
点与点在直线的同侧
连接 , .
则四边形为所求的矩形.
根据上面设计的尺规作图过程,(1)、使用直尺和圆规,在图中补全图形保留作图痕迹;
(2)、完成下面的证明:
证明: , ,
四边形是平行四边形填推理的依据
直线 ,
▲ ,
四边形是矩形填推理的依据 .17.(1)、已知线段 , 求作 , 使得;(请用尺规作图,保留作图痕迹,不写作法.) (2)、求证:直角三角形斜边上的中线等于斜边的一半.(请借助上一小题所作图形,在完善的基础上,写出已知、求证与证明.)18. 如图所示,四边形是半圆O的内接四边形,是半圆O的直径,点C是弧的中点,请仅用无刻度的直尺,按下列要求作图.(保留作图痕迹)
(2)、求证:直角三角形斜边上的中线等于斜边的一半.(请借助上一小题所作图形,在完善的基础上,写出已知、求证与证明.)18. 如图所示,四边形是半圆O的内接四边形,是半圆O的直径,点C是弧的中点,请仅用无刻度的直尺,按下列要求作图.(保留作图痕迹) (1)、在图(1)中,作一个等腰三角形;(2)、在图(2)中,作一个以为对角线的矩形.
(1)、在图(1)中,作一个等腰三角形;(2)、在图(2)中,作一个以为对角线的矩形.四、解答题
-
19. 已知是的直径,点是上一点,点是外一点,是的切线,为切点,连接 , .
 (1)、如图 , 若与相切,为切点, , 求的大小;(2)、如图 , 若与相交于点 , 恰有 , 且 , , 求的长.20. 如图,在中, , 是边的中线,平分的外角 , , 垂足为 .
(1)、如图 , 若与相切,为切点, , 求的大小;(2)、如图 , 若与相交于点 , 恰有 , 且 , , 求的长.20. 如图,在中, , 是边的中线,平分的外角 , , 垂足为 .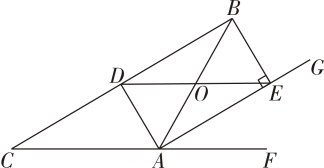 (1)、求证:四边形是矩形;
(1)、求证:四边形是矩形;
(2)、连接 , 交于点 , 若 , , 则的面积是: .21. 如图,在平行四边形中,点是边上一点不与 , 重合 , 过点作 , 交边于点 , 且 , . (1)、求证:四边形是矩形;
(1)、求证:四边形是矩形;
(2)、求证: .五、综合题
-
22. 如图 , 正方形的边长为 , 为边上一动点点与点 , 不重合 , 连接交对角线于点 , 过点作交于点 , 连接 .
 (1)、求证:;
(1)、求证:;
(2)、如图 , 过点作于 , 在点的运动过程中,的长度是否发生变化?若不变,求出的长;若变化,请说明变化规律.
(3)、证明:在点的运动过程中,总有成立.