【北师大版·数学】2024年中考一轮复习之众数

试卷更新日期：2023-11-20 类型：一轮复习

进入出卷网下载

一、选择题

1. 某公司5名员工在一次义务募捐中的捐款额为(单位：元)：30，50，50，60，60.若捐款最少的员工又多捐了20元，则分析这5名员工捐款额的数据时，不受影响的统计量是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
2. 五名同学在“爱心捐助”活动中，捐款数额如下 $($ 单位：元 $)$ ： $8$ ， $10$ ， $10$ ， $4$ ， $6$ ，这组数据的中位数和众数分别是（）

A、 $6$ 和 $8$ B、 $8$ 和 $10$ C、 $9$ 和 $8$ D、 $10$ 和 $8$

查看试题解析
3. 下列说法正确的是（）

A、随机抛掷硬币 $10$ 次，一定有 $5$ 次正面向上
B、一组数据 $8$ ， $9$ ， $10$ ， $11$ ， $11$ 的众数是 $10$
C、为了了解某电视节目的收视率，宜采用抽样调查
D、甲、乙两射击运动员分别射击 $10$ 次，他们成绩的方差分别为 $S_{甲}^{2} = 4$ ， $S_{乙}^{2} = 9$ ，在这过程中，乙发挥比甲更稳定

查看试题解析
4. “青年大学习”是共青团中央为组织引导广大青少年，深入学习贯彻习近平新时代中国特色社会主义思想的青年学习行动 $.$ 某校为了解同学们某季度学习“青年大学习”的情况，从中随机抽取 $7$ 位同学，经统计他们的学习时间 $($ 单位：分钟 $)$ 分别为： $75$ ， $80$ ， $82$ ， $80$ ， $80$ ， $85$ ， $88 .$ 则这组数据的众数为（）

A、 $75$ B、 $80$ C、 $82$ D、 $85$

查看试题解析
5. 垃圾分类是对垃圾进行有效处置的一种科学管理方式，是对垃圾收集处置传统方式的改革，甲乙两班各有 $50$ 名同学参加了学校组织的 $2022$ 年“生活垃圾分类回收”的考试 $.$ 考试规定成绩大于等于 $86$ 分为优异，两个班成绩的平均数、中位数、方差如表所示，则下列说法正确的是（）

参加人数
平均数
中位数
方差
甲
          $50$
          $85$
          $83$
          $5.1$
乙
          $50$
     $85$
     $85$
     $4.6$

A、甲班的成绩比乙班的成绩稳定 B、小高得 $84$ 分将排在甲班的前 $25$ 名
C、甲、乙两班竞赛成绩的众数相同 D、甲班成绩优异的人数比乙班多

查看试题解析

6. 我校

《

足球

》

社团有

30

名成员，下表是社团成员的年龄分布统计表，对于不同的

x

，下列关于年龄的统计量不会发生改变的是（）

年龄 $($ 单位：岁 $)$	$11$	$12$	$13$	$14$	$15$
频数 $($ 单位：名 $)$	$5$	$12$	$x$	$11 - x$	$2$

A、平均数、中位数 B、平均数、方差 C、众数、中位数 D、众数、方差

查看试题解析

7. 为了解学生课外阅读情况，某校随机抽取了一个班的50名学生，对他们一周的课外阅读时间进行了统计，统计数据如下表，则该班学生一周课外阅读时间的中位数和众数分别是（）
读书时间
6小时及以下
7小时
8小时
9小时
10小时及以上
学生人数
5
12
10
13
10

A、10，9 B、10，13 C、8，13 D、8，9

查看试题解析
8. 某次比赛中，五位同学答对题目的个数分别为 $7$ ， $5$ ， $3$ ， $5$ ， $10$ ，则关于这组数据的说法正确的是（）

A、方差是 $3.6$ B、众数是 $10$ C、中位数是 $3$ D、平均数是 $6$

查看试题解析
9. 水是生命之源．为了倡导节约用水，随机抽取某小区7户家庭上个月家里的用水量情况（单位：吨），数据为：7，5，6，8，9，9，10．这组数据的中位数和众数分别是（）

A、9，8 B、9，9 C、8.5，9 D、8，9

查看试题解析
10. 一组数据： $1$ ， $2$ ， $5$ ， $0$ ， $2$ ，若添加一个数据 $2$ ，则发生变化的统计量是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析

二、填空题

11. 我市体育中考有必考和选考项目，掷实心球是必考项目之一，在一次训练中，张华同学掷实心球10次的成绩依次是（单位：米）7.6，8.5，8.6，8.5，9.1，8.5，8.4，8.6，9.2，73．则张华同学撰实心球成绩的众数是．

查看试题解析
12. 小张在“阳光大课间”活动中进行了5次一分钟跳绳练习，所跳个数分别为：160，163，160，157，160．这组数据的众数为．

查看试题解析
13. 在一次体育达标测试中，某小组6名学生的立定跳远成绩如下：9， $x$ ， 6，6，8，4．其中这组数据的众数是6和8，则这组数据的中位数是．

查看试题解析
14. 已知一组数据：6、a、3、4、8、7的众数为6，则这组数据的中位数是．

查看试题解析

三、解答题

15. 二十四节气起源于黄河流域，是古代汉族劳动人民长期经验的积累和智慧的结晶，以二十四节气为核心形成了独具特色的传统文化 $.$ 某校七年级开展了一次“二十四节气知识竞赛”，从 $800$ 名学生成绩中随机抽取了若干名学生的成绩，用得到的数据绘制了如图所示的统计图．
请回答下列问题：

(1)、共抽取七年级名学生的成绩；

(2)、抽取学生成绩的众数和中位数各是多少？

(3)、若得分 $6$ 分及以上为合格，请估计七年级 $800$ 名学生中竞赛成绩达到“合格”的人数．

查看试题解析

16. 学期即将结束，王老师对自己任教的两个班

(

每个班均为

40

人

)

的数学成绩进行质量检测，并对成绩进行统计，得出相关统计表和统计图．其中，成绩均为整数，满分

100

分，成绩等级分为：优秀

(80

分及以上

)

，良好

(70 ～ 79

分

)

，合格

(60 ～ 69

分

)

，不合格

(60

分以下

) . (2)

班中良好这一组学生的成绩分别是：

70

，

71

，

73

，

73

，

73

，

74

，

76

，

77

，

78

，

79

．

$(1)$ 班成绩数据	平均数	众数	中位数	优秀率
人数	$79$	$84$	$76$	$40 %$

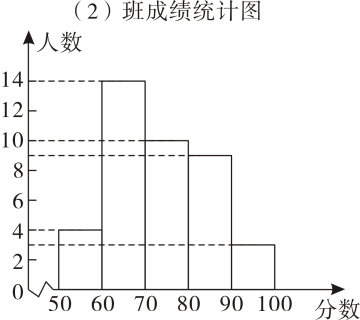
根据以上信息，回答下列问题，

(1)、写出

(2)

班良好这一组成绩的中位数和众数；

(2)、已知

(1)

班没有

3

人的成绩相同，则成绩是

76

分的学生，在哪个班的名次更好些？请说明理由；

(3)、根据上述信息，推断班整体成绩更好，并从两个不同角度说明推断的合理性．

查看试题解析

17. 某小组对当地

2022

年

3

月至

10

月西红柿与黄瓜市场价格进行调研，经过整理、描述和分析得到了部分信息．

a .

西红柿与黄瓜市场价格的折线图：

b .

西红柿与黄瓜价格的众数和中位数：

蔬菜价格	众数	中位数
西红柿 $($ 元 $/$ 千克 $)$	$6$	$m$
黄瓜 $($ 元 $/$ 千克 $)$	$n$	$6$

根据以上信息，回答下列问题：

(1)、

m =

，

n =

；

(2)、在西红柿与黄瓜中，的价格相对更稳定；

(3)、如果这两种蔬菜的价格随产量的增大而降低，结合题中信息推测这两种蔬菜在月的产量相对更高．

查看试题解析

四、综合题

18. 某校舞蹈队共16名学生，测量并获取了所有学生的身高（单位：cm），数据整理如下：
a.16名学生的身高：

161，162，162，164，165，165，165，166，

166，167，168，168，170，172，172，175

b.16名学生的身高的平均数、中位数、众数：

平均数

中位数

众数

166.75

m

n

(1)、写出表中m，n的值；

(2)、对于不同组的学生，如果一组学生的身高的方差越小，则认为该组舞台呈现效果越好．据此推断：在下列两组学生中，舞台呈现效果更好的是（填“甲组”或“乙组”）；
甲组学生的身高
162
165
165
166
166
乙组学生的身高
161
162
164
165
175

(3)、该舞蹈队要选五名学生参加比赛．已确定三名学生参赛，他们的身高分别为168，168，172，他们的身高的方差为 $\frac{32}{9}$ ．在选另外两名学生时，首先要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的方差小于 $\frac{32}{9}$ ，其次要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的平均数尽可能大，则选出的另外两名学生的身高分别为和．

查看试题解析

19. 2023年5月30日，神舟十六号载人飞船成功发射，为大力弘扬航天精神，普及航天知识，激发学生探索和创新热情，某初中在全校开展航天知识竞赛活动现采用简单随机抽样的方法从每个年级抽取相同数量的学生答题成绩进行分析，绘制成下列图表，请根据图表提供的信息，解答下列问题：

学生参加航天知识竞赛成绩频数分布表

竞赛成绩x（组别）	$x < 75$ （A）	$75 \leq x < 80$ （B）	$80 \leq x < 85$ （C）	$85 \leq x < 90$ （D）	$90 \leq x < 95$ （E）	$95 \leq x \leq 100$ （F）
频数	21	96	a	57	b	6

学生参加航天知识竞赛成绩统计表

年级	平均数	众数	中位数
七年级	$\begin{array}{l} 82.73 \end{array}$	82	81
八年级	$\begin{array}{l} 81.84 \end{array}$	82	82
九年级	$\begin{array}{l} 81.31 \end{array}$	83	80

(1)、

a =

；

m =

%；

(2)、请根据“学生参加航天知识竞赛成绩统计表”对本次竞赛中3个年级的总体情况做出评价，并说明理由．

查看试题解析

20. 毛泽东同志曾说“德志皆寄予于体，无体是无德志也”，某社区为了加强社区居民对冬奥会的了解，通过网络宣传冬奥会知识，并鼓励社区居民在线参与作答

《 2022

年北京冬奥会知识点

》

模拟试卷，社区管理员随机从甲、乙两个小区各抽取

20

名人员的答卷成绩，并对他们的成绩

(

单位：分

)

进行统计、分析，过程如下：

收集数据

甲小区： $85 | 80 | 95 | 100 | 90 | 95 | 85 | 65 | 75 | 85 | 89 | 90 | 70 | 90 | 100 | 80 | 80 | 90 | 96 | 75$

乙小区： $80 | 60 | 80 | 95 | 65 | 100 | 90 | 85 | 85 | 80 | 95 | 75 | 80 | 90 | 70 | 80 | 95 | 75 | 100 | 90$

整理数据

成绩 $x ($ 分 $)$	$60 \leq x \leq 70$	$70 < x \leq 80$	$80 < x \leq 90$	$90 < x \leq 100$
甲小区	$2$	$5$	$a$	$b$
乙小区	$3$	$7$	$5$	$5$

分析数据

统计量	平均数	中位数	众数
甲小区	$85.75$	$87$	$c$
乙小区	$83.5$	$d$	$80$

应用数据

(1)、填空：

a =

，

b =

，

c =

，

d =

；

(2)、若甲小区共有

600

人参与答卷，请估计甲小区成绩大于

80

分的人数；

(3)、根据以上数据分析，你认为甲、乙两个小区哪一个对冬奥会知识掌握更好？请写出理由．

查看试题解析

	参加人数	平均数	中位数	方差
甲	$50$	$85$	$83$	$5.1$
乙	$50$	$85$	$85$	$4.6$

读书时间	6小时及以下	7小时	8小时	9小时	10小时及以上
学生人数	5	12	10	13	10

甲组学生的身高	162	165	165	166	166
乙组学生的身高	161	162	164	165	175