【北师大版·数学】2024年中考一轮复习之一次函数的实际应用

试卷更新日期：2023-11-20 类型：一轮复习

进入出卷网下载

一、选择题

1. 武汉市推出上网课包月制，每月收取上网课费用 $y ($ 单位：元 $)$ 与上网时间 $x ($ 单位：小时 $)$ 的函数关系如图所示 $.$ 若小明三月份在家上网课的费用为78元，则他三月份在家上网课的时间为（）

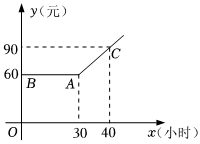A、32小时 B、35小时 C、36小时 D、38小时

查看试题解析
2. 如图，多边形的各顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形，它的面积S可用公式 $S = a + \frac{1}{2} b - 1$ （a是多边形内的格点数，b是多边形边界上的格点数）计算，这个公式称为皮克定理，若有一个格点多边形的面积为9，则b的最大值为（）

A、17 B、18 C、19 D、20

查看试题解析
3. 如图是温度计的示意图，图中左边的温度表示摄氏温度，右边的温度表示华氏温度．小明观察温度计发现，两个刻度x，y之间的关系如下表：
x/℃
10
20
25
30
y/℉
50
68
77
86
据此可知，摄氏温度为15时，对应的华氏温度应为（）

A、15 B、59 C、-9.4 D、54

查看试题解析
4. 如图，已知A、B两地相距20km，甲从A地出发到B地，一段时间后，乙从B地出发到A地，甲、乙两人离A地的距离 $s (k m)$ 与甲所用的时间 $t (h)$ 之间的关系如图所示，则他们相遇时距离A地（）

A、8km B、10km C、12km D、14km

查看试题解析
5. 如图，一个弹簧不挂重物时长6cm，挂上重物后，在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长y（单位：cm）关于所挂物体质量x（单位：kg）的函数图象如图所示，则图中a的值是（）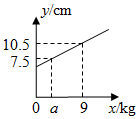

A、3 B、4 C、5 D、6

查看试题解析
6. 如图，用弹簧测力计将一铁块悬于盛有水的水槽中，然后匀速向上提起，使铁块完全露出水面，并上升一定高度，则下列能反映弹簧测力计的读数y（单位：N）与铁块被提起的时间x（单位：s）之间的函数关系的大致图象是（　　）

A、 B、 C、 D、

查看试题解析
7. 皮克定理是格点几何学中的一个重要定理，它揭示了以格点为顶点的多边形的面积 $S = N + \frac{1}{2} L - 1$ ，其中 $N ， L$ 分别表示这个多边形内部与边界上的格点个数．在平面直角坐标系中，横、纵坐标都是整数的点为格点．已知 $A (0 ， 30)$ ， $B (20 ， 10) ， O (0 ， 0)$ ，则 $△ A B O$ 内部的格点个数是（）

A、266 B、270 C、271 D、285

查看试题解析
8. 某产品的盈利额（即产品的销售价格与固定成本之差）记为y，购买人数记为x，其函数图象如图1所示．由于日前该产品盈利未达到预期，相关人员提出了两种调整方案，图2，图3中的实线分别为调整后y与x的函数图象．给出下列四种说法，其中正确说法的序号是（　　）
①图2对应的方案是：保持销售价格不变，并降低成本；

②图2对应的方案是：提高销售价格，并提高成本；

③图3对应的方案是：提高销售价格，并降低成本

④图3对应的方案是：提高销售价格，并保持成本不变

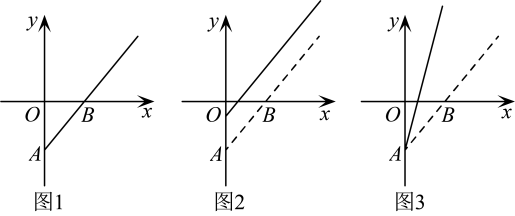A、①③ B、②③ C、①④ D、②④

查看试题解析
9. 一个小球沿一个斜坡上下滚动，其速度v（单位： $m / s$ ）与时间t（单位：s）的图象如图所示．下列说法错误的是（）

A、小球的初始速度为 $6 m / s$ B、小球先沿斜坡向上滚动，再沿斜坡向下滚动 C、当 $3 \leq t \leq 6$ 时，小球的速度每秒增加 $2 m / s$ D、小球在整个滚动过程中，当 $t = 3$ 时，到达斜坡的最低处

查看试题解析
10. 如图1，在 $▱ A B C D$ 中，点M，N同时从点B出发，点M以 $\sqrt{3} c m / s$ 的速度沿B→A→D→C匀速运动到点C，点N以1cm/s的速度沿BC匀速运动到点C，当其中一点到达终点时，另一点也随之停止运动.设点M的运动路程长为 $x (c m)$ ， $△ B M N$ 的面积为 $y (c m^{2})$ ， y与x的函数图象如图2所示，当运动时间为 $\frac{8}{3} s$ 时， $△ B M N$ 的面积是（） $c m^{2}$ .

A、 $\frac{7}{4}$ B、 $\frac{3}{2}$ C、 $\frac{3 \sqrt{3}}{2}$ D、 $\frac{4 \sqrt{3}}{3}$

查看试题解析

二、填空题

11. 同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数解析式是y＝ $\frac{9}{5}$ x＋32.若某一温度的摄氏度数值与华氏度数值恰好相等，则此温度的摄氏度数为℃.

查看试题解析
12. 大连市内与庄河两地之间的距离是160千米，若汽车以平均每小时80千米的速度从大连市内开往庄河，则汽车距庄河的路程y(千米)与行驶的时间x(小时)之间的函数关系式为．

查看试题解析

13. 声音在空气中的传播速度

v (m / s)

与温度

t (℃)

的关系如表：

温度 $(℃)$	$0$	$5$	$10$	$15$	$20$
速度 $v (m / s)$	$331$	$336$	$341$	$346$	$351$

则速度 $v$ 与温度 $t$ 之间的关系式为；当 $t = 30 ℃$ 时，声音的传播速度为 $m / s$ ．

查看试题解析

14. 如图，某电信公司提供了A、B两种方案的移动通讯费用y（元）与通话时间x（元）之间的关系．如果通讯费用为60元，那么A方案与B方案的通话时间相差分钟．

查看试题解析
15. 在平面直角坐标系中,点P（x₀ ， y₀）到直线Ax+By+C=0的距离公式为: $d = \frac{| A x_{0} + B y_{0} + C |}{\sqrt{A^{2} + B^{2}}}$ ,则点P（3，-3）到直线 $y = - \frac{2}{3} x + \frac{5}{3}$ 的距离为.

查看试题解析

三、解答题

16. 为了解某新能源汽车的充电速度，某数学兴趣小组经研究发现：如图，用快速充电器时，汽车电池电量 $y_{1} ($ 单位： $%)$ 与充电时间 $x ($ 单位： $h)$ 的函数图象是折线 $A B C$ ；用普通充电器时，汽车电池电量 $y_{2} ($ 单位： $%)$ 与充电时间 $x ($ 单位： $h)$ 的函数图象是线段 $A D .$
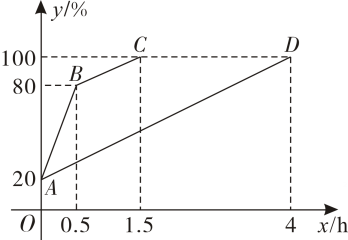
根据以上信息，回答下列问题：

(1)、普通充电器对该汽车每小时的充电量为 $%$ ；

(2)、求 $y_{1}$ 与 $x$ 的函数解析式，并写出 $x$ 的取值范围；

(3)、若将该汽车电池电量从 $20 %$ 充至 $90 %$ ，快速充电器比普通充电器少用 $h .$

查看试题解析
17. 广西平陆运河北起横州市西津水电站库区平塘江口，南止于钦江出海口沙井港航道，在一航道建设中，某渣土运输公司承包了某标段的土方运输任务，拟派出大、小两种型号的渣土运输车运输土方 $.$ 已知 $5$ 辆大型渣土运输车与 $2$ 辆小型渣土运输车一次共运输土方 $60$ 吨， $6$ 辆大型渣土运输车与 $4$ 辆小型渣土运输车一次共运输土方 $80$ 吨．

(1)、一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨？

(2)、该渣土运输公司决定派出大、小两种型号渣土运输车共 $20$ 辆参与把 $156$ 吨土方全部运走，若一辆大型渣土运输车耗费 $600$ 元，一辆小型渣土运输车耗费 $400$ 元，请你设计出最省钱的运输方案．

查看试题解析

18. 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．

已知小明家、体育馆、图书馆依次在同一条直线上

.

小明从家出发，匀速骑行

0.5 h

到达体育馆；在体育馆停留一段时间后，匀速步行

0.4 h

到达图书馆；在图书馆停留一段时间后，匀速骑行返回家中，给出的图象反映了这个过程中小明离开家的距离

y k m

与离开家的时间

x h

之间的对应关系．
请根据相关信息，解答下列问题：

(1)、填表：

小明离开家的时间 $/ h$	$0.1$	$0.3$	$1.5$	$2.2$	$3.3$
小明离开家的距离 $/ k m 1.2$	$1.2$	▲	$6$	▲	▲

(2)、填空：

①

体育馆与图书馆之间的距离为 ▲

k m

；

②

小明从体育馆到图书馆的步行速度为 ▲

k m / h

；

③

当小明离开家的距离为

4 k m

时，他离开家的时间为 ▲

h .

(3)、当

2 \leq x \leq 4

时，请直接写出

y

关于

x

的函数解析式．

查看试题解析

四、综合题

19. 某市全面实施居民“阶梯水价”．当累计水量超过年度阶梯水量分档基数临界点后，即开始实施阶梯价格计价，分档水量和单价见下表：

分档	户年用水量（立方米）	自来水单价（元/立方米）	污水处理单价（元/立方米）
第一阶梯	0~220（含220）	2.25	1.8
第二阶梯	220~300（含300）	4
第三阶梯	300以上	6.99
注：应缴的水费＝户年用水量×（自来水单价＋污水处理单价）

仔细阅读上述材料，请解答下面的问题：

(1)、如果小叶家全年用水量是220立方米，那么她家全年应缴纳水费多少元？

(2)、居民应缴纳水费y（元）关于户年用水量x（立方米）的函数关系如图所示，求第二阶梯（线段

A B

）的表达式；

(3)、如果小明家全年缴纳的水费共计1181元，那么他家全年用水量是多少立方米？

查看试题解析

20. 为满足顾客的购物需求，某水果店计划购进甲、乙两种水果进行销售.经了解，甲水果的进价比乙水果的进价低20%，水果店用1000元购进甲种水果比用1200元购进乙种水果的重量多10千克，已知甲，乙两种水果的售价分别为6元/千克和8元/千克.

(1)、求甲、乙两种水果的进价分别是多少？

(2)、若水果店购进这两种水果共150千克，其中甲种水果的重量不低于乙种水果重量的2倍，则水果店应如何进货才能获得最大利润，最大利润是多少？

查看试题解析
21. 如图（1）所示，小明家、食堂、图书馆在同一条直线上食堂离小明家 $0.6 k m$ ，图书馆离小明家 $0.8 k m$ ．小明从家出发，匀速步行了 $8 m i n$ 去食堂吃早餐；吃完早餐后接着匀速步行了 $3 m i n$ 去图书馆读报；读完报以后接着匀速步行了 $10 m i n$ 回到家图（ $2$ ）反映了这个过程中，小明离家的距离 $y$ 与时间 $x$ 之间的对应关系．
请根据相关信息解答下列问题：

(1)、填空：
①食堂离图书馆的距离为 $k m$ ；
②小明从图书馆回家的平均速度是 $k m / m i n$ ；
③小明读报所用的时间为 $m i n$ ．
④小明离开家的距离为 $\frac{2}{3} k m$ 时，小明离开家的时间为 $m i n$ ．

(2)、当 $0 \leq x \leq 28$ 时，请直接写出 $y$ 关于 $x$ 的函数解析式．

查看试题解析

x/℃	10	20	25	30
y/℉	50	68	77	86