(人教版)2024年中考数学一轮复习 方程与不等式--不等式与不等式组 练习题
试卷更新日期:2023-11-20 类型:一轮复习
一、选择题
-
1. “与的积加上不小于”用不等式表示是( )A、 B、 C、 D、2. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、3. 不等式的解集在数轴上表示正确的是( )A、
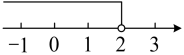 B、
B、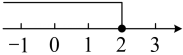 C、
C、 D、
D、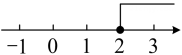 4. 某校九年级班学生小聪家和小明家到学校的直线距离分别是和那么小聪,小明两家的直线距离不可能是( )A、 B、 C、 D、5. 点 , 在数轴上的位置如图所示,点 , 表示的有理数为 , 如果 , , 那么下列描述数轴原点的位置说法正确的是( )
4. 某校九年级班学生小聪家和小明家到学校的直线距离分别是和那么小聪,小明两家的直线距离不可能是( )A、 B、 C、 D、5. 点 , 在数轴上的位置如图所示,点 , 表示的有理数为 , 如果 , , 那么下列描述数轴原点的位置说法正确的是( ) A、原点在点左侧 B、原点在点的右侧 C、原点在点、之间,且 D、原点在点、之间,且6. 设x , y , c为实数,则下列说法正确的是( )A、若x>y , 则x+3c>y-2c B、若x>y , 则xc>yc C、若x>y , 则xc2>yc2 D、若 , 则x>y7. 若m>n , 则下列不等式中正确的是( )A、m-2<n-2 B、mn C、n-m>0 D、1-2m<1-2n8. 乌鞘岭是陇中高原和河西走廊的天然分界,主峰海拔超过米若用米表示乌鞘岭主峰的海拔高度,则满足的关系为( )A、 B、 C、 D、9. 已知 , 则a和b的关系是( )A、 B、 C、 D、不能确定10. 已知药品A的保存温度要求为 , 药品B保存温度要求为 , 若需要将A , B两种药品放在一起保存,则保存温度要求为( )A、 B、 C、 D、
A、原点在点左侧 B、原点在点的右侧 C、原点在点、之间,且 D、原点在点、之间,且6. 设x , y , c为实数,则下列说法正确的是( )A、若x>y , 则x+3c>y-2c B、若x>y , 则xc>yc C、若x>y , 则xc2>yc2 D、若 , 则x>y7. 若m>n , 则下列不等式中正确的是( )A、m-2<n-2 B、mn C、n-m>0 D、1-2m<1-2n8. 乌鞘岭是陇中高原和河西走廊的天然分界,主峰海拔超过米若用米表示乌鞘岭主峰的海拔高度,则满足的关系为( )A、 B、 C、 D、9. 已知 , 则a和b的关系是( )A、 B、 C、 D、不能确定10. 已知药品A的保存温度要求为 , 药品B保存温度要求为 , 若需要将A , B两种药品放在一起保存,则保存温度要求为( )A、 B、 C、 D、二、填空题
-
11. 不等式的解集为 .12. 不等式组的解集是 .13. 若关于的不等式组恰有个整数解,则实数的取值范围是 .14. 不等式组的解集为 , 则m的取值范围为 .15. 根据年8月日太原市市政府公布的《太原市推进城市空间立体绿化实施方案》,某小区积极进行小区绿化,计划种植A,B两种苗木共株.已知A种苗木的数量不小于B种苗木的数量的一半,若设A种苗木有x株,则可列不等式:.

三、解答题
-
16. 解不等式组并写出它的所有整数解.17. 已知实数m是一个不等于2的常数,解不等式组 ,并根据m的取值情况写出其解集.18. 先化简,再求值:
( ﹣1)÷ ,其中x的值从不等式组 的整数解中选取.
19.(1)、有三个不等式 , , , 请在其中任选两个不等式,组成一个不等式组,并求出它的解集;
(2)、小红在计算时,解答过程如下:第一步
第二步
第三步小红的解答从第 步开始出错,请写出正确的解答过程.
四、综合题
-
20. 解不等式组 请结合题意填空,完成本题的解答.(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来:
 (4)、原不等式组的解集为.21. 建设美丽城市,改造老旧小区.某市2019年投入资金1000万元,2021年投入资金1440万元,现假定每年投入资金的增长率相同.(1)、求该市改造老旧小区投入资金的年平均增长率;(2)、2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质,每个小区改造费用增加15%.如果投入资金年增长率保持不变,求该市在2022年最多可以改造多少个老旧小区?22.(1)、已知不等式 , 请你写出一个不等式 , 使它与已知不等式组成的不等式组的解集为 .(2)、在数学活动课上,老师出了一道一元二次方程的试题:“”让同学们解答,甲、乙两位同学的做法如下:
(4)、原不等式组的解集为.21. 建设美丽城市,改造老旧小区.某市2019年投入资金1000万元,2021年投入资金1440万元,现假定每年投入资金的增长率相同.(1)、求该市改造老旧小区投入资金的年平均增长率;(2)、2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质,每个小区改造费用增加15%.如果投入资金年增长率保持不变,求该市在2022年最多可以改造多少个老旧小区?22.(1)、已知不等式 , 请你写出一个不等式 , 使它与已知不等式组成的不等式组的解集为 .(2)、在数学活动课上,老师出了一道一元二次方程的试题:“”让同学们解答,甲、乙两位同学的做法如下:甲同学
乙同学
解:原方程可化为: ,
解:原方程可化为: ,
当时,解得 ,
,
当时,解得 ,
,
∴ , .
∴ ,
∴ , .
小组在交流过程中发现甲、乙两位同学的结果不同,请判断哪位同学的做法有误(填“甲”或“乙”),并根据该同学使用的方法写出正确的解答过程.
23. 春暖花开正是郊游踏青的好时节.为开阔学生视野,一班的家委会准备利用周末组织该班学生参加郊游活动,计划在某商家采购A、B两种水果各600元,其中A种水果比B种水果多买20千克,该商家B种水果的单价是A种水果单价的1.5倍.(1)、求A、B两种水果的单价分别是多少元?(2)、经过家委会和商家协商,商家决定给该班购买的A、B两种水果进行优惠,将A、B两种水果都打8折,因此,家长将调整购买计划,购买A、B两种水果共150千克,但购买的总费用不能超过1500元,则至少购买A种水果多少千克?