云南省文山州丘北县2023-2024学年九年级上学期第一次月考数学试卷

试卷更新日期：2023-11-20 类型：月考试卷

进入出卷网下载

一、选择题（每小题3分，共36分）

1. 方程x²=3x的解为（）

A、x=3 B、x=0 C、x₁=0，x₂=﹣3 D、x₁=0，x₂=3

查看试题解析
2.
如图，下列条件中，能使▱ABCD成为菱形的是（　　）

A、AB=CD B、AD=BC C、AB=BC D、AC=BD

查看试题解析
3. 如图，某小区居民休闲娱乐中心是一块长方形（长60米，宽40米）场地，被3条宽度相等的绿化带分为总面积为1750平方米的活动场所，如果设绿化带的宽度为x米，由题意可列方程为（）

A、（60-x）（40-x）＝1750 B、（60-2x）（40-x）＝1750 C、（60-2x）（40-x）＝2400 D、（60-x）（40-2x）＝1750

查看试题解析
4. 如图，在菱形 $A B C D$ 中，点 $E$ 是 $A B$ 的中点，点 $F$ 是 $A C$ 的中点，连接 $E F$ ，如果 $E F = 4$ ，那么菱形 $A B C D$ 的周长为（）

A、4 B、8 C、16 D、32

查看试题解析
5. 在数学活动课上，老师和同学们判断一个四边形门框是否为矩形.下面是某个合作小组的4位同学拟定的方案，其中正确的是（）

A、测量对角线是否互相平分 B、测量两组对边是否分别相等 C、测量其内角是否均为直角 D、测量对角线是否垂直

查看试题解析
6. 用配方法解方程3x²-6x-1＝0，则方程可变形为（）

A、（x-3）²＝ $\frac{1}{3}$ B、（x-1）²＝ $\frac{1}{3}$ C、（3x-1）²＝1 D、（x-1）²＝ $\frac{4}{3}$

查看试题解析
7. 已知三角形其中两边之和为10，第三边长是方程x²-12x+11＝0的一个根，则该三角形的周长为（）

A、11 B、21 C、11或21 D、11或1

查看试题解析
8. 如图，在矩形纸片 $A B C D$ 中， $A B = 6$ ， $B C = 8$ ，点 $E$ 是 $A B$ 上一点，点 $F$ 是 $B C$ 上一点，将矩形沿 $E F$ 折叠，使点 $B$ 的对应点 $G$ 正好落在 $A D$ 的中点处，则 $A E$ 的长为（　　）

A、 $\frac{5}{6}$ B、 $\frac{5}{3}$ C、2 D、3

查看试题解析
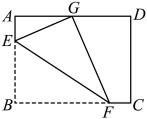9. 距考试还有20天的时间，为鼓舞干劲，老师要求班上每一名同学要给同组的其他同学写一份拼搏进取的留言，小明所在的小组共写了30份留言，该小组共有（）

A、7人 B、6人 C、5人 D、4人

查看试题解析
10. 在菱形ABCD中，AE⊥BC于点E，AF⊥CD于点F，且E，F分别为BC，CD的中点，（如图）则∠EAF等于（）

A、75° B、45° C、60° D、30°

查看试题解析
11. 关于x的一元二次方程x²-2x-3＝0有两个实数根m，n，那么一次函数y＝mnx+m+n的图象一定不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
12. 已知关于x的一元二次方程x²-mx+n＝0，其中m，n在数轴上的对应点如图所示，则这个方程的根的情况是（）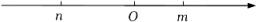

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析

二、填空题（每小题2分，共8分）

13. 若a是一元二次方程x²+2x-3＝0的一个根，则2a²+4a的值是．

查看试题解析
14. 若正方形的一条对角线长为 $2 \sqrt{2}$ ，则该正方形的周长为．

查看试题解析
15. 某市某楼盘准备以每平方米7200元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，为了加快资金周转，房地产开发商对价格经过两次下调后，决定以每平方米5832元的均价开盘销售．则平均每次下调的百分率为．

查看试题解析
16. 如图，正方形ABCD的边长为1，以对角线AC为边作第二个正方形，再以对角线AE为边作第三个正方形AEGH，如此下去，第n个正方形的边长为．

查看试题解析

三、解答题：（共9题，共56分）

17. 解方程：（x+2）²-x-2＝0．

查看试题解析
18. 如图，在菱形 $A B C D$ 中，点E是边 $A D$ 上一点，延长 $A B$ 至点F，使 $B F = A E$ ，连接 $B E ， C F$ ．求证： $∠ A E B = ∠ F$ ．

查看试题解析
19. 已知关于x的一元二次方程x²+（m+3）x+m+2＝0．

(1)、求证：无论m取何值，原方程总有两个实数根；

(2)、若x₁ ， x₂是原方程的两根，且x₁²+x₂²＝2，求m的值．

查看试题解析
20. 如图，在△ABC中，∠ACB＝90°，D为AB的中点．过点C作CE∥BD，过点D作DE∥BC，且DE，CE交于点E，连接AE，试判断四边形ADCE的形状，并证明你的结论．

查看试题解析
21. 在学习《完全平方公式》时，某数学学习小组发现：已知a+b＝5，ab＝3，可以在不求a、b的值的情况下，求出a²+b²的值．具体做法如下：
a²+b²＝a²+b²+2ab-2ab＝（a+b）²-2ab＝5²-2×3＝19．

(1)、若a+b＝7，ab＝6，则a²+b²＝；

(2)、若m满足（8-m）（m-3）＝3，求（8-m）²+（m-3）²的值，同样可以应用上述方法解决问题．具体操作如下：
解：设8-m＝a，8-m＝a，m-3＝b，
则a+b＝（8-m）+（m-3）＝5，a+b＝（8-m）+（m-3）＝5，ab＝（8-m）（m-3）＝3，
所以（8-m）²+（m-3）²＝a²+b²＝（a+b）²-2ab＝5²-2×3＝19．
请参照上述方法解决下列问题：若（3x-2）（10-3x）＝6，求（3x-2）²+（10-3x）²的值；

查看试题解析
22. 如图，在菱形ABCD中，对角线AC与BD交于点O．过点C作BD的平行线，过点D作AC的平行线，两直线相交于点E．

(1)、求证：四边形OCED是矩形；

(2)、若CE＝1，DE＝2，则菱形ABCD的面积是．

查看试题解析
23. 党的二十大报告指出：“全面推进乡村振兴，坚持农业农村优先发展，坚持城乡融合发展，畅通城乡要素流动．”畅通城乡经济循环被摆在突出位置，成为当前和今后阶段全面推进乡村振兴的重要目标，福建某县市通过网络直播带货助力乡村振兴，打响绿色经济发展攻坚战役，某直播间销售某种“特色农产品”，每箱获利40元，每天可卖出30箱，通过市场调查发现：每箱“特色农产品”的售价每降低1元，每天的销售量就增加3箱．

(1)、若每箱“特色农产品”的售价降低3元，求每天的销售量．

(2)、为尽快减少库存，决定降价销售，若要使得每天获利1800元，则每箱“特色农产品”的售价需降低多少元？

查看试题解析
24. 如图所示，四边形ABCD为矩形，AB＝6cm，AD＝4cm，若点Q从A点出发沿AD以1cm/s的速度向D运动，P从B点出发沿BA以2cm/s的速度向A运动，如果P、Q分别同时出发，当一个点到达终点时，另一点也同时停止．设运动的时间为t（s）．

(1)、当t为何值时，△PDQ的面积为6cm²？

(2)、是否存在t使△PDQ为等腰三角形？若存在，求出t值；若不存在，请说明理由．

查看试题解析