吉林省长春市榆树市2023-2024学年八年级上学期期中数学试卷
试卷更新日期：2023-11-20 类型：期中考试
一、选择题（每小题3分，共24分）
-
1. 9的平方根是（ ）A、-3 B、3 C、±3 D、±92. 在实数- ， 0， ， 3.14中，无理数是（ ）A、- B、0 C、 D、3.143. 能与数轴上的点一一对应的是（ ）A、整数 B、有理数 C、无理数 D、实数4. 下列计算正确的是（ ）A、m3+m2＝m5 B、m6÷m2＝m3 C、（m3）2＝m9 D、m3•m2＝m55. 下列命题是假命题的是（ ）A、两边及其夹角分别相等的两个三角形全等 B、两角及其夹边分别相等的两个三角形全等 C、两边分别相等且其中一组等边的对角相等的两个三角形全等 D、两角分别相等且其中一组等角的对边相等的两个三角形全等6. 已知x，y满足 ， 则x2-9y2的值为（ ）A、-5 B、4 C、5 D、257. 如图，AB＝AC，AD＝AE，∠A＝105°，∠D＝25°，则∠ABE等于（ ）
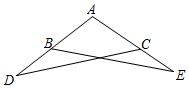A、65° B、60° C、55° D、50°8. 使（x2+px+8）（x2﹣3x+q）乘积中不含x2与x3项的p、q的值是（ ）A、p=0，q=0 B、p=3，q=1 C、p=﹣3，q=﹣9 D、p=﹣3，q=1二、填空题（每小题3分，共18分）
-
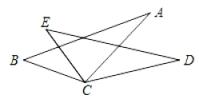
9. -0.008的立方根是 ．10. 多项式6ab2x-3a2by+12a2b2的公因式是 ．11. 以a＝为反例可以证明命题“对任意实数a它的平方是正数”是假命题，12. 已知3m＝2，3n＝5，则32m+n的值是 ．13. 如图，∠ACD＝∠BCE，BC＝EC，要使△ABC≌△DEC，则可以添加的一个条件是 ．
14. 如图，CA⊥AB于点A，DB⊥AB于点B，AB＝12m．AC＝4m，点P从点B出发，向终点A运动，每分钟走1m，点Q从点B出发．沿射线BD运动，每分钟走2m．P、Q两点同时出发，当点P到达点A时，P、Q同时停止运动．设运动时间是x分钟，当x＝时，△CAP与△PQB全等．
三、简答题（本大题共10小题，共78分）
-
15. 计算：(1)、(2)、（-3x+2）（-3x+6）；(3)、（6x3-15x2+3x）÷3x．16. 把下列多项式分解因式：(1)、a2x2-a2y2 ．(2)、4x2-8xy+4y2 ．17. 利用乘法公式计算：(1)、20192-2018×2020．(2)、99.82 ．18. 如图，点B，F，C，E在同一条直线上，BF＝CE，∠B＝∠E，∠ACB＝∠DFE．求证：△ABC≌△DEF．
19. 先化简，再求值：（a+b）（a-b）+a（2b-a），其中a＝ ， b＝-2．20. 已知a+＝3，求：
(1)、a2+；(2)、a- ．21. 如图，某市有一块长为 米，宽为 米的长方形地，规划部门将阴影部分进行绿化，中间将修建一座边长为 米的正方形水池．
(1)、试用含 ， 的式子表示绿化部分的面积（结果要化简）．(2)、求出当 ， 时的绿化面积．22. 如图，点E在边AC上，已知AB＝DC，∠A＝∠D，BC∥DE．
求证：
(1)、△ABC≌△DCE；(2)、DE＝AE+BC．23. 探究与应用我们学习过（x-1）（x+1）＝x2-1，那么（x-1）（x6+x5+x4+x3+x2+x+1）计算结果呢？
完成下面的探究：
(1)、（x-1）（x2+x+1）＝；(2)、（x-1）（x3+x2+x+1）＝；……(3)、（x-1）（x6+x5+x4+x3+x2+x+1）＝；(4)、应用：计算2+22+23+24+……+22022 ．24. 有一张边长为a厘米的正方形桌面，因为实际需要，需将正方形边长增加b厘米，木工师傅设计了如图所示的三种方案：善于观察思考的小明发现：利用图形面积关系这三种方案都能验证公式：a2+2ab+b2＝（a+b）2 ．
对于方案一，小明是这样验证的：
因为大正方形的面积可以看成：a2+ab+ab+b2＝a2+2ab+b2 ， 又可以看成（a+b）2 ， 所以a2+2ab+b2＝（a+b）2 ．
解答下列问题：(1)、公式验证：请根据方案二、方案三，分别写出公式的验证过程．方案二：；
方案三：；
(2)、公式应用，已知实数a，b均为正数，且a-b＝2，ab＝3，求a+b的值．