吉林省松原市长岭县2023-2024学年八年级上学期期中数学试卷
试卷更新日期：2023-11-20 类型：期中考试
一、选择题（每小题2分，共20分）
-
1. 冬季奥林匹克运动会是世界上规模最大的冬季综合性运动会，下列四个图是历届冬奥会图标中的一部分，其中是轴对称图形的为（ ）A、
B、
C、
D、
2. 在平面直角坐标系中，若点P（a-3，1）与点Q（2，b+1） 关于x轴对称， 则a+b的值是（ ）A、1 B、2 C、3 D、43. 若长度分别为a，3，5的三条线段能组成一个三角形，则a的值可以是（ ）A、1 B、2 C、3 D、84. 如图，在△ABC中，AD是△ABC的角平分线， DE⊥AC， 若∠B＝40°，∠C＝60°，则∠ADE的度数为（ ）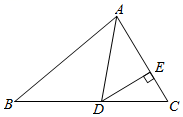
A、30° B、40° C、50° D、60°5. 如图，在△ABC和△DCB中，∠ACB＝∠DBC， 添加一个条件， 不能证明△ABC和△DCB全等的是（ ）
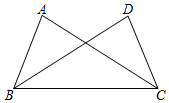A、∠ABC＝∠DCB B、AB＝DC C、AC＝DB D、∠A＝∠D6. 如图，在△ABC中，AB＝BC， ∠BAC=120°， AB的垂直平分线交AB于点E，交BC于点F， 若BF=2， 则CF的长为（ ）
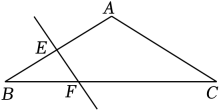A、2 B、4 C、6 D、8二、填空题（每小题3分，共24分）
-
7. 一个多边形的每个外角都等于与它相邻的内角，这个多边形是边形．8. 等腰三角形的两边长分别为8，6，这个三角形的周长为 ．9. 如图，在△ABC中，∠C＝70°，则∠1+∠2＝ ．
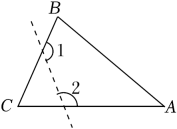10. 如图，△ABC中，AD是BC边上的中线， BE是△ABC中AD边上的中线， 若△ABC的面积是24，AE＝6，则点B到ED的距离是 ．
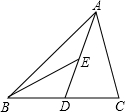11. 如图，在△ABC中，∠ABC和∠ACB的平分线交于点O， 若∠BOC=130°， 则∠A＝ ．
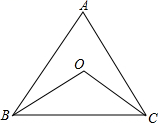12. 如图，某轮船以20海里/时的速度自西向东航行，在A处测得有一小岛P在北偏东60°的方向上，航行了2小时到达B处， 这时间得该小岛P在北偏东30°的方向上，则轮船在B处时与小岛P的距离是海里．
13. 如图，等腰直角三角形ABC的直角顶点C与坐标原点重合，分别过点A、B作x轴的垂线， 垂足为D、E， 点A的坐标为（-2，5），则线段DE的长为 ．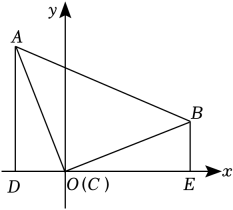
14. 如图，△ABC中，AB＝AC， 分别以A、B为圆心， 以适当的长为半径作弧，两弧分别交于E、F，D为BC的中点，M为直线EF上任意一点， 若BC=4， △ABC的面积为10，则BM+MD的最小值是 ．
三、解答题（每小题5分，共20分）
-
15. 如图，△ABC中，AD⊥BC，∠B＝40°，∠C＝70°，求∠DAE的度数．
16. 已知：如图，点A，D，C在同一直线上， AB∥EC， AC＝CE，∠B+∠ADE＝180°．求证：BC＝DE．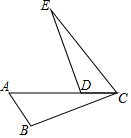
17. 如图，六边形ABCDEF是轴对称图形，CF所在的直线是它的对称轴， 若∠AFC+∠BCF=150°， 求∠D+∠E的度数．
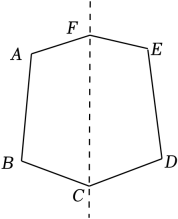18. 如图，已知D为BC的中点，DE⊥AB， DF⊥AC， 点E，F为垂足， 且BE=CF， ∠BDE＝30°，求证：△ABC是等边三角形．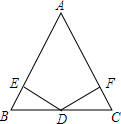
四、解答题（每选题7分，共28分）
-
19. 如图，把△ABC放置在4×4的正方形网格纸中，三角形的顶点都在格点上．在网格纸中用三种不同的方法画出与△ABC有一条公共边，且与△ABC成轴对称的三角形（要求顶点都在格点上）．
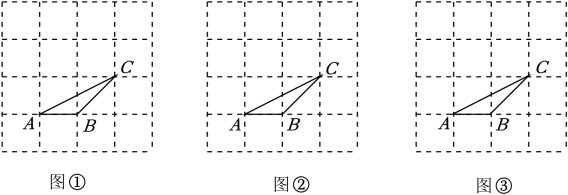20. 如图，∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE和BD相交于点O.
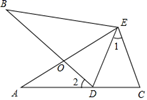(1)、求证：△AEC≌△BED；(2)、若∠1＝48°，求∠BDE的度数.21. 如图，在△ABC中，AB＝CB， ∠ABC=90°， D为AB延长线上一点，点E在BC边上， 且BE=BD， 连接AE、DE、DC．
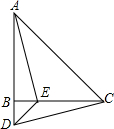(1)、求证：△ABE≌△CBD；(2)、若∠CAE＝30°，求∠BDC的度数．22.如图，DE⊥AB于E，DF⊥AC于F，若BD=CD、BE=CF．
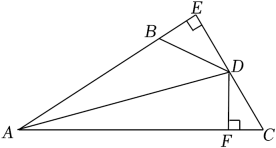(1)、求证：AD平分∠BAC；(2)、已知AC＝10，BE＝2，求AB的长．五、解答题（每题题8分，共16分）
-
23.
如图所示，在等边三角形ABC中，P、Q是BC边上的两点，AP=AQ，∠BAP=20°．
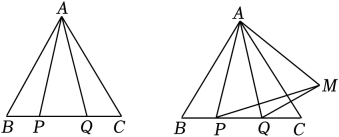(1)、求∠AQB的度数；(2)、在（1）的条件下，点Q关于直线AC的时称点为M， 连接MM、PM、QC， 求证：AP＝PM．24. 如图
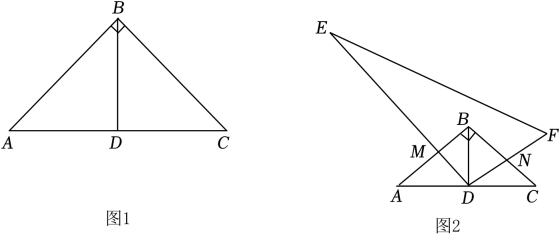(1)、特例探究：如图1，已知在△ABC中，AB＝CB， ∠ABC=90°， D为AC边的中点，连接BD，△ABD是什么三角形？(2)、归纳证明：如图2，已知在△ABC中，AB=CB，∠ABC=90°，D为AC边的中点，连接BD，把Rt△DEF的直角顶点D放在AC的中点上，DE交AB于M，DF交BC于N．证明：DM=DN．(3)、拓展应用：如图2，AC＝2m（m＞0）其他条件都不发生变化，则Rt△DEF与△ABC的重叠部分的面积是（用含m的代数式表示）．六、解答题（每道题10分，共20分）
-
25. 如图，在△ABC中，AB=AC=2，∠B=∠C=40°，点D在线段BC上运动（D不与B、C重合），连接AD，作∠ADE=40°，DE交线段AC于E．
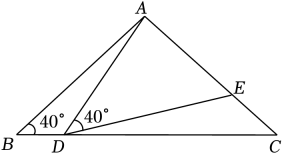(1)、当∠BDA＝115°时，∠EDC＝ ， ∠DEC＝；(2)、当DC等于多少时，△ABD≌△DCE，请说明理由；(3)、在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，请直接写出∠BDA的度数．若不可以 ，请说明理由．26. 如图①，点P、Q分别是边长为4cm的等边边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，设运动时间为t（s).
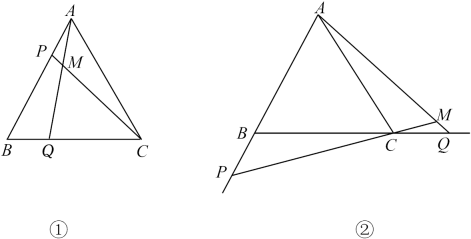(1)、当t＝s时，△PBQ是等边三角形；(2)、连接AQ、CP，交于点M，则在P、Q运动的过程中， ∠CMQ的度数是否发生变化？若变化，说明理由；若不变，请求出它的度数；(3)、求t为何值时，△PBQ是直角三角形；(4)、如图②，若点P、Q在运动到终点后继续在射线AB、BC上向前运动，直线AQ、CP交于点M ，请直接写出∠CMQ的度数．