吉林省松原市前郭县北片名校调研2023-2024学年九年级上学期期中数学试卷
试卷更新日期：2023-11-20 类型：期中考试
一、选择题（每小题2分，共12分）
-
1. 抛物线y＝3x2+2的顶点坐标是（ ）A、（0，2） B、（-2，0） C、（2，0） D、（0，-2）2. 下列环保标志图案既是轴对称图形，又是中心对称图形的是（ ）A、
B、
C、
D、
3. 广东春季是流感的高发时期，某校4月初有一人患了流感，经过两轮传染后，共25人患流感，假设每轮传染中平均每人传染x人，则可列方程 （ ）A、1+x+x2＝25 B、x+x2＝25 C、（1+x）2＝25 D、x+x（1+x）＝254. 已知实心球运动的高度y（m）与水平距离x（m）之间的函数关系是y＝-（x-1）2+4，则该同学此次投掷实心球的成绩是（ ）
A、2m B、3m C、3.5m D、4m5. 如图△ABC中，∠C=90°，∠B=20°，以C为圆心，CA为半径的圆交AB于点D， 则的度数为（ ）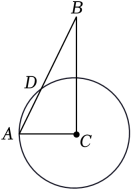
A、30° B、40° C、45° D、50°6. 如图，△ABC中，∠BAC=135°，把△ABC绕着点C顺时针旋转得到△DEC，若点D、A、B恰好在一条直线上，则下列结论错误的是 （ ）
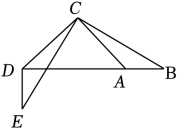A、ED⊥BD B、△ABC≌△DEC C、 D、BD＝CE+DE二、填空题（每小题3分，共24分）
-
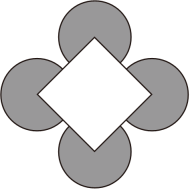
7. 点M（-3，2）关于原点对称的点的坐标是 ．8. 如图所示的图形绕其中心至少旋转度就可以与原图形完全重合．
9. 二次函数y＝-3（x+1）2的最大值为 ．10. 已知⊙O的半径为2cm ， 则⊙O最长的弦为cm ．11. 用配方法解一元二次方程x2-6x＝1时，可将原方程配方成（x-m）2＝n ， 则m+n的值是 ．12. 如图，A、B、C为⊙O上三点，若∠AOB＝140°，则∠ACB度数为°．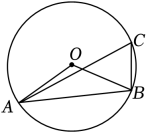
13. 如图，在平面直角坐标系中，点B坐标（8，4）， 连接OB， 将OB绕点O逆时针旋转90°，得到OB'，则点B′的坐标为 ．
14. 如图，已知二次函数y＝ax2+bx+c的图象过点（3，0），对称轴为直线x＝1，则下列结论：①abc＜0；②ax2+bx+c＝0的两个根是x1＝-1，x2＝3；③当x＜1时，y随着x的增大而增大 ；④4a+2b+c＜0． （填写序号）．
三、解答题（每小题5分，共20分）
-
15. 用适当的方法解方程：x2-2x-8＝0．16. 已知二次函数y＝ax2（a≠0）的图象经过点（2，-1），求该函数的解析式及对称轴．17. 如图，在△ABD中，∠BAD=90°，将△ABD绕点A逆时针旋转后得到△ACE，C点落在BD边上，若∠E=17°，求∠BAC的度数．
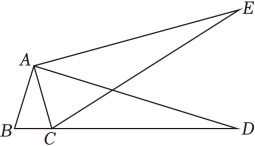18. 在平面直角坐标系中，抛物线y＝ax2-（a+4）x+3经过点（2，-3）．(1)、求此抛物线的解析式；(2)、当1＜x＜5时，直接写出y的取值范围．四、解答题（每小题7分，共28分）
-
19. 如图，在6×6方格纸中，已知格点P和格点线段AC，请按要求画出以AC为对角线的格点四边形（顶点均在格点上），且点P在四边形内部（不包括边界上）．
(1)、在图1中画出一个▱ABCD；(2)、在图2中画出一个四边形AECF ， 使得点P落在四边形某一边的中垂线上，且四边形中有且仅有两个内角为直角．20. “筒车”是一种以水流作动力，取水灌田的工具，如图，“筒车”盛水筒的运行轨迹是以轴心O为圆心的圆，已知圆心O始终在水面上方，且当圆被水面截得的弦AB为6米时，水面下盛水筒的最大深度为1米（即水面下方部分圆上的一点距离水面的最大距离），求该圆的半径．
21. 如图，方格纸中每个小正方形的边长都是1个单位长度，在方格纸中建立如图所示的平面直角坐标系，△OAB的顶点都在格点上，已知点A（-4，-2），B（-2，-6）．
⑴将△OAB向右平移4个单位长度得到△O1A1B1 ， 请画出△O1A1B1；
⑵将△OAB绕点O顺时针旋转90°，画出所得的△OA2B2 ．22. 若二次函数 的图象经过点A（-2，0），其对称轴为直线x=1，与x轴的另一个交点为C，与y轴交于点B．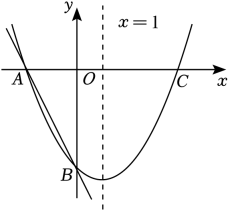
(1)、点C的坐标为；(2)、将二次函数的图象向下平移5个单位长度，求平移后的二次函数的解析式．五、解答题（每小题8分，共16分）
-
23. 如图，圆内接四边形ABCD的对角线AC，BD交于点E，BD平分∠ABC，∠BAC=∠ADB．
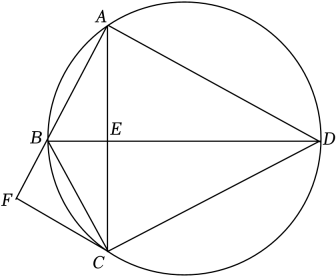(1)、求证DB平分∠ADC ， 并求∠BAD的大小；(2)、过点C作CF∥AD交AB的延长线于点F ， 若AC＝AD ， BF＝2求此圆半径的长24. 阅读与理解：图1是边长分别为a和b（a＞b）的两个等边三角形纸片ABC和C′DE叠放在一起（点C与点C′重合）的图形．
操作与证明：
(1)、操作：固定△ABC，将△C′DE绕点C按顺时针方向旋转30°，连接AD，BE，如图2，在图2中，线段BE与AD之间具有怎样的大小关系？证明你的结论；(2)、操作：若将图1中的△C′DE，绕点C按顺时针方向任意旋转一个角度α，连接AD，BE，如图3，在图3中，线段BE与AD之间具有怎样的大小关系？证明你的结论；(3)、猜想与发现：
根据上面的操作过程，请你猜想当α为多少度时，线段AD的长度最大，最大是多少？当α为多少度时，线段AD的长度最小，最小是多少？六、解答题（每小题10分，共20分）
-
25. 如图，在菱形ABCD中，∠A=60°，AB=4cm，点P从点A出发，以2cm/s的速度沿折线AB-BC向终点C运动；同时点Q从点A出发，以相同的速度沿折线AD-DC向终点C运动，连接PQ，过点Q作AB的平行线 ，并截取QM＝QP ， 且点M在点Q的右侧，以PQ、QM为邻边作▱PQMN，设▱PQMN与菱形ABCD重叠部分图形的面积为y（cm2），点P的运动时间为x（s）（0＜x＜4）．
(1)、当点N与点B重合时，x的值为；(2)、求PQ的长（用含x的代数式表示）；(3)、求y关于x的函数关系式，并写出自变量x的取值范围26. 在平面直角坐标系中，O为坐标原点，点A（-1，0），B（0，-）在抛物线y=x2+bx+c上，点C为该抛物线的顶点，点P为该抛物线上一点 ，其横坐标为m.
(1)、求该抛物线对应的函数关系式；(2)、连接BP ， 当BP⊥y轴时，顺次连接点A、B、C、P ，求四边形ABCP的面积 ；(3)、当m＞0时，设该抛物线在点B与点P之间（包含点B和点P）的部分图象的最低点和最高点到x轴的距离分别为k、n ， 若k-n=2， 求m的取值范围．