山东省泰安市宁阳县2023-2024学年九年级上学期期中考试数学试卷
试卷更新日期:2023-11-20 类型:期中考试
一、单选题(每题4分,共计48分)
-
1. 在如图所示的几何体中,其主视图、左视图和俯视图完全相同的是( )A、
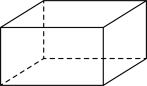 B、
B、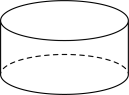 C、
C、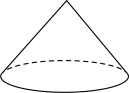 D、
D、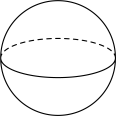 2. 下列函数是二次函数的是( )A、y=ax2+bx+c B、y=(2x﹣1)2﹣4x2 C、 D、y=(x﹣1)(x﹣2)3. 若反比例函数y=的图象分布在第二、四象限,则k的取值范围是( )A、k< B、k> C、k>2 D、k<24. 正在建设中的临滕高速是我省“十四五”重点建设项目.一段工程施工需要运送土石方总量为 , 设土石方日平均运送量为V(单位:/天),完成运送任务所需要的时间为t(单位:天),则V与t满足( )A、反比例函数关系 B、正比例函数关系 C、一次函数关系 D、二次函数关系5. 小乐用一块长方形硬纸板在阳光下做投影试验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是( )A、三角形 B、线段 C、矩形 D、正方形6. 将二次函数y=﹣2x2的图象平移后,可得到二次函数y=﹣2(x+1)2的图象,平移的方法是( )A、向上平移1个单位 B、向下平移1个单位 C、向左平移1个单位 D、向右平移1个单位7. 把二次函数y=﹣x2﹣x+3用配方法化成y=a(x﹣h)2+k的形式时,应为( )A、y=﹣(x﹣2)2+2 B、y=﹣(x﹣2)2+4 C、y=﹣(x+2)2+4 D、y=﹣(x﹣)2+38. 将一个大正方体的一角截去一个小正方体,得到的几何体如图所示,则该几何体的左视图是( )
2. 下列函数是二次函数的是( )A、y=ax2+bx+c B、y=(2x﹣1)2﹣4x2 C、 D、y=(x﹣1)(x﹣2)3. 若反比例函数y=的图象分布在第二、四象限,则k的取值范围是( )A、k< B、k> C、k>2 D、k<24. 正在建设中的临滕高速是我省“十四五”重点建设项目.一段工程施工需要运送土石方总量为 , 设土石方日平均运送量为V(单位:/天),完成运送任务所需要的时间为t(单位:天),则V与t满足( )A、反比例函数关系 B、正比例函数关系 C、一次函数关系 D、二次函数关系5. 小乐用一块长方形硬纸板在阳光下做投影试验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是( )A、三角形 B、线段 C、矩形 D、正方形6. 将二次函数y=﹣2x2的图象平移后,可得到二次函数y=﹣2(x+1)2的图象,平移的方法是( )A、向上平移1个单位 B、向下平移1个单位 C、向左平移1个单位 D、向右平移1个单位7. 把二次函数y=﹣x2﹣x+3用配方法化成y=a(x﹣h)2+k的形式时,应为( )A、y=﹣(x﹣2)2+2 B、y=﹣(x﹣2)2+4 C、y=﹣(x+2)2+4 D、y=﹣(x﹣)2+38. 将一个大正方体的一角截去一个小正方体,得到的几何体如图所示,则该几何体的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 已知点A(﹣2,y1),B(﹣1,y2),C(1,y3)均在反比例函数y=的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y1<y2 D、y3<y2<y110. 如图,下列选项中,能描述函数y=ax2与y=ax+a的图象可能是( )A、
9. 已知点A(﹣2,y1),B(﹣1,y2),C(1,y3)均在反比例函数y=的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y1<y2 D、y3<y2<y110. 如图,下列选项中,能描述函数y=ax2与y=ax+a的图象可能是( )A、 B、
B、 C、
C、 D、
D、 11. 如图,矩形OABC与反比例函数y1=(k1是非零常数,x>0)的图象交于点M , N , 与反比例函数y2=(k2是非零常数,x>0)的图象交于点B , 连接OM , ON . 若四边形OMBN的面积为3,则k1﹣k2=( )
11. 如图,矩形OABC与反比例函数y1=(k1是非零常数,x>0)的图象交于点M , N , 与反比例函数y2=(k2是非零常数,x>0)的图象交于点B , 连接OM , ON . 若四边形OMBN的面积为3,则k1﹣k2=( ) A、3 B、﹣3 C、 D、12. 如图,是二次函数y=ax2+bx+c图象的一部分,则a的取值范围是( )
A、3 B、﹣3 C、 D、12. 如图,是二次函数y=ax2+bx+c图象的一部分,则a的取值范围是( )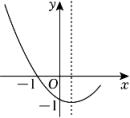 A、a>1 B、a>2 C、0<a<1 D、0<a<2
A、a>1 B、a>2 C、0<a<1 D、0<a<2二、填空题(每题4分,共计24分)
-
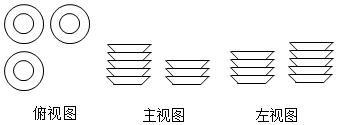
13. 反比例函数的图象经过点 , 则反比例函数的表达式为 .14. 如果抛物线y=x2﹣6x+c与x轴只有一个交点,那么c的值是 .15. 在一张桌子上摆放着一些碟子,从3个方向看到的3种视图如图所示,则这个桌子上的碟子共有个.
 16. 某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,且当时, . 当气球内的气体压强大于时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于 .17. 如图,在直线l:y=x﹣4上方的双曲线y=(x>0)上有一个动点P , 过点P作x轴的垂线,交直线l于点Q , 连接OP , OQ , 则△POQ面积的最大值是 .
16. 某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,且当时, . 当气球内的气体压强大于时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于 .17. 如图,在直线l:y=x﹣4上方的双曲线y=(x>0)上有一个动点P , 过点P作x轴的垂线,交直线l于点Q , 连接OP , OQ , 则△POQ面积的最大值是 .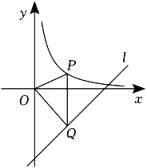 18. 下列关于二次函数y=﹣(x﹣m)2+m2+1(m为常数)的结论:①该函数的图象与函数y=﹣x2的图象形状相同;②该函数的图象一定经过点(0,1);③当x>0时,y随x的增大而减小;④该函数的图象的顶点在函数y=x2+1的图象上.其中所有正确结论的序号是 .
18. 下列关于二次函数y=﹣(x﹣m)2+m2+1(m为常数)的结论:①该函数的图象与函数y=﹣x2的图象形状相同;②该函数的图象一定经过点(0,1);③当x>0时,y随x的增大而减小;④该函数的图象的顶点在函数y=x2+1的图象上.其中所有正确结论的序号是 .三、解答题(共78分)
-
19. 如图,在平面直角坐标系中,O为坐标原点,直线交y轴于点A , 交x轴于点B , 与双曲线在一,三象限分别交于C , D两点, , 连接 , .
 (1)、求k的值;(2)、求的面积.20. 如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.
(1)、求k的值;(2)、求的面积.20. 如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.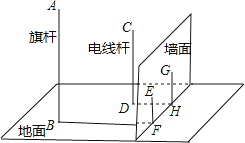 (1)、该小组的同学在这里利用的是 投影的有关知识进行计算的;(2)、试计算出电线杆的高度,并写出计算的过程。
(1)、该小组的同学在这里利用的是 投影的有关知识进行计算的;(2)、试计算出电线杆的高度,并写出计算的过程。
21. 某工艺品厂设计了一款每件成本为11元的工艺品投放市场进行试销,经过市场调查,得出每天销售量y(件)是每件售价x(元)(x为正整数)的一次函数,其部分对应数据如下表所示:每件售价x(元)
…
15
16
17
18
…
每天销售量y(件)
…
150
140
130
120
…
(1)、求y关于x的函数解析式;(2)、若用w(元)表示工艺品厂试销该工艺品每天获得的利润,试求w关于x的函数解析式;(3)、该工艺品每件售价为多少元时,工艺品厂试销该工艺品每天获得的利润最大,最大利润是多少元?22. 如图,一次函数y=x+5的图象与反比例函数y=(k为常数且k≠0)的图象相交于A(﹣1,m),B两点. (1)、求反比例函数的表达式;(2)、将一次函数y=x+5的图象沿y轴向下平移b个单位(b>0),使平移后的图象与反比例函数y=的图象有且只有一个交点,求b的值.23. 许多数学问题源于生活.雨伞是生活中的常用物品,我们用数学的眼光观察撑开后的雨伞(如图①)、可以发现数学研究的对象——抛物线.在如图②所示的直角坐标系中,伞柄在y轴上,坐标原点O为伞骨OA , OB的交点.点C为抛物线的顶点,点A , B在抛物线上,OA , OB关于y轴对称.OC=1分米,点A到x轴的距离是0.6分米,A , B两点之间的距离是4分米.
(1)、求反比例函数的表达式;(2)、将一次函数y=x+5的图象沿y轴向下平移b个单位(b>0),使平移后的图象与反比例函数y=的图象有且只有一个交点,求b的值.23. 许多数学问题源于生活.雨伞是生活中的常用物品,我们用数学的眼光观察撑开后的雨伞(如图①)、可以发现数学研究的对象——抛物线.在如图②所示的直角坐标系中,伞柄在y轴上,坐标原点O为伞骨OA , OB的交点.点C为抛物线的顶点,点A , B在抛物线上,OA , OB关于y轴对称.OC=1分米,点A到x轴的距离是0.6分米,A , B两点之间的距离是4分米.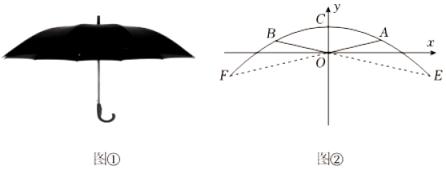 (1)、求抛物线的表达式;(2)、分别延长AO , BO交抛物线于点F , E , 求E , F两点之间的距离.24. 如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点和x轴正半轴上的点B , AO=OB .
(1)、求抛物线的表达式;(2)、分别延长AO , BO交抛物线于点F , E , 求E , F两点之间的距离.24. 如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点和x轴正半轴上的点B , AO=OB .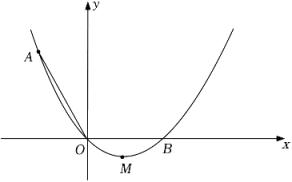 (1)、求这条抛物线的表达式;(2)、连接OM , 求∠AOM的度数;(3)、连接AM、BM、AB , 若在坐标轴上存在一点P , 使∠OAP=∠ABM , 求点P的坐标.25. 如图,抛物线y=ax2+bx﹣6与x轴相交于A , B两点,与y轴相交于点C , OA=2,OB=4,直线l是抛物线的对称轴,在直线l右侧的抛物线上有一动点D , 连接AD , BD , BC , CD .
(1)、求这条抛物线的表达式;(2)、连接OM , 求∠AOM的度数;(3)、连接AM、BM、AB , 若在坐标轴上存在一点P , 使∠OAP=∠ABM , 求点P的坐标.25. 如图,抛物线y=ax2+bx﹣6与x轴相交于A , B两点,与y轴相交于点C , OA=2,OB=4,直线l是抛物线的对称轴,在直线l右侧的抛物线上有一动点D , 连接AD , BD , BC , CD .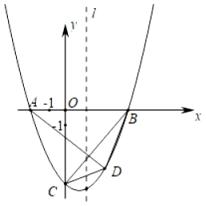 (1)、求抛物线的函数表达式;(2)、若点D在x轴的下方,当△BCD的面积是时,求△ABD的面积;(3)、在(2)的条件下,点M是x轴上一点,点N是抛物线上一动点,是否存在点N , 使得以点B , D , M , N为顶点,以BD为一边的四边形是平行四边形,若存在,求出点N的坐标;若不存在,请说明理由.
(1)、求抛物线的函数表达式;(2)、若点D在x轴的下方,当△BCD的面积是时,求△ABD的面积;(3)、在(2)的条件下,点M是x轴上一点,点N是抛物线上一动点,是否存在点N , 使得以点B , D , M , N为顶点,以BD为一边的四边形是平行四边形,若存在,求出点N的坐标;若不存在,请说明理由.