四川省绵阳市涪城区2023-2024学年九年级上学期期中教学质量监测数学试卷

试卷更新日期：2023-11-20 类型：期中考试

进入出卷网下载

一、选择题:本大题共12个小题，每小题3分，共36分.在每个小题给出的四个选项中，只有一个是符合题目要求的.

1. 在一元二次方程-x²-4x+1＝0中，二次项系数和一次项系数分别是（　　）

A、-1，4 B、-1，-4 C、1，4 D、1，-4

查看试题解析
2. 用配方法解方程x²+2x-5＝0时，下列配方结果正确的是（　　）

A、（x-1）²＝5 B、（x-1）²＝6 C、（x+1）²＝7 D、（x+1）²＝6

查看试题解析
3. 下面图形是用数学家名字命名的，其中是中心对称图形但不是轴对称图形的是（）

A、赵爽弦图 B、笛卡尔心形线 C、科克曲线 D、斐波那契螺旋线

查看试题解析
4. 巴人广场中心标志性建筑处有高低不同的各种喷泉，其中一支高度为1米的喷水管最大喷水高度为3米，此时喷水水平距离为 $\frac{1}{2}$ 米，在如图所示的坐标系中，这支喷泉的函数关系式是（　　）

A、 $y = - {(x - \frac{1}{2})}^{2} + 3$ B、 $y = 3 {(x - \frac{1}{2})}^{2} + 1$ C、 $y = - 8 {(x - \frac{1}{2})}^{2} + 3$ D、 $y = - 8 {(x + \frac{1}{2})}^{2} + 3$

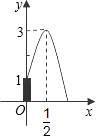查看试题解析
5. 下列关于x的一元二次方程中有两个相等的实数根的是（　　）

A、（x-3）²＝4 B、x²＝x C、x²+2x+1＝0 D、x²-16＝0

查看试题解析
6. 某商场第1年销售计算机5000台，如果每年的销售量比上一年增加相同的百分率x ，第3年的销售量为y台，则y关于x的函数解析式为（　　）

A、y＝5000（1+2x） B、y＝5000（1+x）² C、y＝5000+2x D、y＝5000x²

查看试题解析
7. 若将一个二次函数的图象向下平移2个单位，再向左平移3个单位，所得函数解析式是y＝ $\frac{1}{2}$ x² ，那么这个函数解析式为（　　）

A、y＝ $\frac{1}{2}$ （x+3）²-2 B、y＝ $\frac{1}{2}$ （x+3）²+2 C、y＝ $\frac{1}{2}$ （x-3）²-2 D、y＝ $\frac{1}{2}$ （x-3）²+2

查看试题解析
8. 如图，在△ABC中，AB＝AC ， ∠A＝30°，D、E分别在AB、AC上，CE＝ $\sqrt{3}$ -1，且△BED是等腰直角三角形，其中∠BED＝90°，则AD的值是（　　）

A、1 B、 $\sqrt{3}$ C、 $\sqrt{3} - 1$ D、 $\frac{\sqrt{3} - 1}{2}$

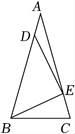查看试题解析
9. 已知关于x的一元二次方程 $x^{2} + 2 m = 4 x$ 有两个不相等的实数根，则m的取值范围是（）

A、m≥2 B、m<2 C、m≥0 D、m<0

查看试题解析
10. 定义新运算：对于两个不相等的实数a ， b ，我们规定符号max{a ， b}表示a ， b中的较大值，如：max{1，3}＝3，因此max{-1，-3}＝-1；按照这个规定，若max{x ， -x}＝ $\frac{x^{2} - 2 x - 1}{2}$ ，则x的值是（　　）

A、-1 B、-1或2+ $\sqrt{5}$ C、2+ $\sqrt{5}$ D、1或2- $\sqrt{5}$

查看试题解析
11. 如图，将Rt△ABC绕着直角顶点A顺时针旋转90°后得到△AB′C′，则∠CC′A的度数为（　　）

A、30° B、45° C、60° D、90°

查看试题解析
12. 对于一个函数，如果它的自变量x与函数值满足：当-1≤x≤1时，-1≤y≤1，则称这个函数为“闭函数”．例如：y＝x ， y＝-x均是“闭函数”．已知y＝ax²+bx+c（a≠0）是“闭函数”且抛物线经过点A（1，-1）和点B（-1，1），则a的取值范围是（　　）

A、 $- \frac{1}{2} \leq a \leq \frac{1}{2}$ B、 $- \frac{1}{2} \leq a < 0$ 或 $0 < a \leq \frac{1}{2}$ C、-1≤a≤1 D、-1≤a＜0或0＜a≤1

查看试题解析

二、填空题（共6小题，每小题4分,满分18分）

13. 若 $y = (n + 2) x^{n^{2} - 2} + n x + 1$ 是关于自变量x的二次函数，则n＝．

查看试题解析
14. 已知点A（3a-9，2-a）关于原点对称的点为A′，点A′关于x轴对称的点为A″，点A″在第四象限，那么a的取值范围是．

查看试题解析
15. 如图，把Rt△ABC绕点A逆时针旋转40°，得到Rt△AB'C'，点C′恰好落在边AB上，连接BB'，则∠C′B'B的度数是．

查看试题解析
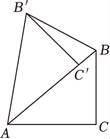16. 如图，正方形EFGH的顶点在边长为2的正方形的边上．若设AE=x，正方形EFGH的面积为y，则y与x的函数关系为．

查看试题解析
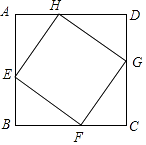17. 如图，点P是等边三角形ABC内的一点，且PA＝ $\sqrt{6}$ ， PB＝ $\sqrt{2}$ ， PC＝2 $\sqrt{2}$ ，则∠APB的度数为．

查看试题解析
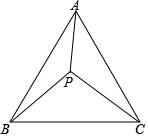18. 如图是二次函数y＝ax²+bx+c图象的一部分，其对称轴是直线x＝-1，且过点（-3，0），有以下结论：①abc＞0；②4a+2b+c＞0；③a-b≤m（am+b）（m为任意实数）；④若方程a（x+3）（1-x）＝-1的两根为x₁ ， x₂ ，且x₁＜x₂ ，则-3＜x₁＜x₂＜1，其中说法正确的有．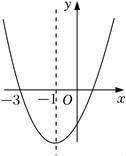

查看试题解析

三、解答题（共6小题，满分46分）

19. 在下面的网格（每个小正方形的边长为1）中按要求画出图形并解答：
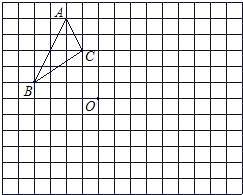
⑴先将△ABC向下平移5格得△A₁B₁C₁ ，再将△ABC以点O为旋转中心，沿顺时针方向旋转90°得△A₂B₂C₂；
⑵请在图中以点O为坐标原点，建立适当直角坐标系，写出此时点A₂、B₂、C₂的坐标．

查看试题解析
20. 如图，已知抛物线y＝-x²+（m-1）x+m的对称轴为x＝1，请你解答下列问题：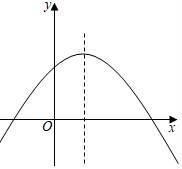

(1)、求m的值；

(2)、求出抛物线与x轴的交点；

(3)、当y随x的增大而减小时x的取值范围．

(4)、当y＜0时，x的取值范围．

查看试题解析
21. 某公司的商品进价每件60元，售价每件130元，为了支持“抗新冠肺炎”，每销售一件捐款4元．且未来30天，该商品将开展每天降价1元”的促销活动，即从第一天起每天的单价均比前一天降1元，市场调查发现，设第x天（1≤x≤30且x为整数）的销量为y件，y与x满足一次函数关系，其对应数据如表：
x（天）
……
1
3
5
7
……
y（件）
……
35
45
55
65
……

(1)、直接写出y与x的函数关系式；

(2)、在这30天内，哪一天去掉捐款后的利润是6235元？

(3)、设第x天去掉捐款后的利润为W元，试求出W与x之间的函数关系式，并求出哪一天的利润最大，最大利润是多少元？

查看试题解析
22. 如图，长为10m的梯子斜靠在墙上，梯子的顶端距地面的垂直距离为8m ．如果梯子的底端滑动1m ，求梯子顶端下滑的区间．（精确到0.1米）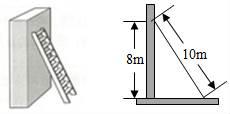

查看试题解析
23. 某学校活动小组探究了如下问题，请你帮助他们完成解答过程：

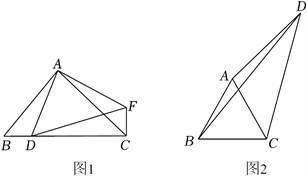(1)、操作发现：如图1，△ABC中，AB＝AC ， ∠BAC＝90°，D为边BC上的一点，连接AD ，作∠FAD＝90°，并截取FA＝AD ，连接DF ．求证：BD²+CD²＝DF²；

(2)、灵活运用：如图2，在四边形ABCD中，AC ， BD是对角线，△ABC是等边三角形，∠ADC＝30°，AD＝3，BD＝5，求CD的长．

查看试题解析
24. 如图，在顶点为P的抛物线y＝a（x-h）²+k（a≠0）的对称轴l上取点A（h ， k+ $\frac{1}{4} a$ ），过A作BC⊥l交抛物线于B、C两点（B在C的左侧），点A′和点A关于点P对称；过A′作直线m⊥l ，又分别过点B、C作BE⊥m和CD⊥m ，垂足为E、D ．在这里我们把点A叫此抛物线的焦点，BC叫此抛物线的直径，矩形BCDE叫此抛物线的焦点矩形．

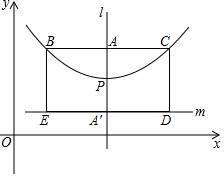(1)、直接写出抛物线y＝ $\frac{1}{4}$ x²的焦点坐标以及直径的长．

(2)、求抛物线y＝ $\frac{1}{4}$ （x-3）²+2的焦点坐标以及直径的长．

(3)、已知抛物线y＝a（x-h）²+k（a≠0）的直径为 $\frac{3}{2}$ ，求a的值．

(4)、①已知抛物线y＝ax²+bx+c（a≠0）的焦点矩形的面积为2，求a的值．
②直接写出抛物线y＝ $\frac{1}{4}$ （x-3）²+2的焦点矩形与抛物线y＝x²-2mx+m²+1有两个公共点时m的取值范围．

查看试题解析

x（天）	……	1	3	5	7	……
y（件）	……	35	45	55	65	……