吉林省白城市通榆九中、育才学校联考2023-2024学年九年级上学期期中数学试卷
试卷更新日期：2023-11-20 类型：期中考试
一、单项选择题（每小题2分，共12分）
-
1. 剪纸艺术是中国最古老的民间艺术之一，先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录．以下剪纸图案中，是中心对称图形的是（ ）A、
B、
C、
D、
2. 抛物线y＝（x-1）2+2的顶点坐标是（ ）A、（1，2） B、（1，-2） C、（-1，2） D、（-1，-2）3. 如图，点A，B，C在⊙O上，若∠AOB=110°，则∠C的度数是（ ）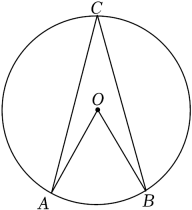
A、110° B、100° C、65° D、55°4. 如图，四边形ABCD是圆内接四边形，∠BAD=108°，E是BC延长线上一点，若∠ECF=60°，则∠DCF的大小是 （ ）
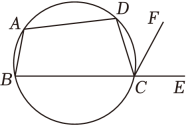A、30° B、48° C、54° D、60°5. 若非零实数a、b、c满足9a-3b+c＝0，则关于x的一元二次方程ax2+bx+c＝0一定有一个根为（ ）A、3 B、-3 C、0 D、无法确定6. “圆材埋壁”是我国古代数学名著《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺．问：径几何？”用现在的几何语言表达即：如图，CD为⊙O的直径，弦AB⊥CD，垂足为点E，CE=1寸，AB=10寸，则直径CD的长度是 （ ）
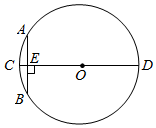A、12寸 B、24寸 C、13寸 D、26寸二、填空题（每小题3分，共24分）
-
7. 点P（-3，2）关于原点O对称的点P1的坐标为 ．8. 一元二次方程x2-x＝0的解是 ．9. 若将方程x2+4x=m化为(x+2)2=5，则m= ．10. 已知抛物线y＝ax2+bx+c与x轴的交点是（-1，0）、（3，0），则这条抛物线的对称轴是 ．11. 已知如图所示的图形的面积为24，则x的值为
12. 如图，E是正方形ABCD内一点，将△ABE绕点B顺时针旋转与△CBF重合，若BE= ， 则EF＝ ．
13. 如图，在△ABC中，∠ACB=90°，AB=5，BC=4，以点A为圆心，r为半径作圆，当点C在⊙A内且点B在⊙A外时，r的值可能是 （写出一个即可）．
14. 我们规定：对于任意实数a，b，c，d有[a，b]*[c，d]=ac-bd，其中等式右边是通常的乘法和减法运算（如：[3，2]*[5，1]=3×5-2×1=13），若[-x，3]*[x-2，-6]=10，则x的值为 ．三、解答题（每小题5分，共20分）
-
15. 解方程：x2-4x+4＝0．16. 如图，在△ABC中，∠A=30°，∠C=90°，BC=1，将△ABC绕点B旋转180°，点A落在点A′处，求AA′的长度．
17. 如图，A，P，B，C是⊙O上的四点，∠APC＝∠CPB＝60°，求证：△ABC是等边三角形．
18. 汽车刹车后行驶的距离s（单位：m）关于行驶的时间t（单位：s）的函数解析式是s＝15t-6t2 ． 汽车刹车后到停下来前进了多远？四、解答题（每小题7分，共28分）
-
19. 如图，A，B，C三点的坐标分别为（﹣4，1），（﹣3，3），（﹣1，﹣1）．
⑴将△ABC绕点O顺时针旋转90°，画出旋转后所得到的△DEF（点D，E，F分别对应点A，B，C）．
⑵画出△DEF关于原点对称的图形△PMN（点P，M，N分别对应点D，E，F）．
⑶直接写出△PMN的面积．
20. 如图是一个正方体的展开图，标注了字母m的面是正方体的正面，若正方体的各个相对面的数字相同，求x的值．
21. 已知，如图，直线l经过A（4，0）和B （0，4）两点，它与抛物线y＝ax2在第一象限内相交于点P，又知△AOP的面积为4，求a的值．
22. 阅读下列材料，回答问题：当抛物线的解析式中含有字母系数时，随着字母的取值的不同，抛物线的顶点坐标也将发生变化．
例如：已知抛物线y＝x2﹣2mx+m2+2m﹣1，①
由①可得y＝（x﹣m）2+2m﹣1，②
所以抛物线y＝x2﹣2mx+m2+2m﹣1的顶点坐标为（m，2m﹣1），即 ．
当m的值变化时，x，y的值也随之变化．将③代入④，得y＝2x﹣1．⑤
可见，不论m取任何实数，抛物线顶点的纵坐标y与横坐标x满足y＝2x﹣1．
(1)、在上述过程中，由①得到②所用的数学方法是 （填“A”或“B”），由③④到⑤所用的数学方法是（填“A”或“B”）．
A.消元法
B.配方法(2)、根据以上材料提供的方法，确定抛物线y＝x2﹣2mx+2m2﹣3m+1顶点的纵坐标y和横坐标x之间的函数关系式．解：y＝x2﹣2mx+2m2﹣3m+1＝（x﹣）2+m2﹣3m+1，
∴此抛物线的顶点坐标为（m，），即 ．
当m的值变化时，x，y的值也随之变化．将①代入②，得y＝x2﹣3x+1．
可见，不论m取任何实数，抛物线顶点的纵坐标y与横坐标x满足 ．
五、解答题（每小题8分，共16分）
-
23. 如图所示，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC，过点D作DE⊥AC于E．
(1)、求证：AB＝AC；(2)、求证：DE为⊙O的切线．24. 小明在复习数学知识时，针对“求一元二次方程的解”，整理了以下的几种方法 ，请你按有关内容补充完整：复习日记卡片
内容：一元二次方程解法归纳时间：2019年6月1日
举例：求一元二次方程x2﹣x﹣2＝0的两个解
方法一：选择合适的一种方法（公式法、配方法、分解因式法）求解
解方程：x2﹣x﹣2＝0．
解：
方法二：利用二次函数图象与坐标轴的交点求解
如图所示，把方程x2﹣x﹣2＝0的解看成是二次函数y＝ ▲ 的图象与x轴交点的横坐标，即x1 ， x2就是方程的解．
方法三：利用两个函数图象的交点求解
（1）把方程x2﹣x﹣2＝0的解看成是一个二次函数y＝ ▲ 的图象与一个一次函数y＝ ▲ 图象交点的横坐标；
（2）画出这两个函数的图象，用x1 ， x2在x轴上标出方程的解．
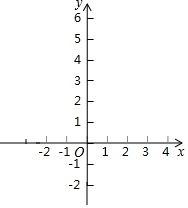
六、解答题（每小题10分，共20分）
-
25. 如图，在矩形ABCD中，AB=2cm，AD=4cm.动点P，Q从A同时出发，且速度均为2cm/s，点P，Q分别沿折线AB-BC，AD-DC向终点C运动．设点P的运动时间为x（s）（0＜x＜3），△APQ的面积为y（cm2）．
(1)、当点P与点B重合时，x的值为 ．(2)、求y关于x的函数解析式，并写出x的取值范围．(3)、当PQ长度不变时，直接写出x的取值范围及PQ的长度．26. 如图，抛物线 上的点A，C的坐标分别为（0，2），（4，0），抛物线与x轴负半轴交于点B，点M为y轴负半轴上一点，且OM=2，连接AC、CM．
(1)、点M的坐标为 ．(2)、求此抛物线的解析式．(3)、点P是抛物线位于第一象限图象上的动点，连接AP、CP，当S△PAC＝S△ACM时，点P的横坐标为 ．(4)、将抛物线沿x轴的负方向平移m（m＞0）个单位长度，得到新抛物线， 点A的对应点为点A′ ，点C的对应点为点C′，在抛物线平移的过程中，①当点C′在线段A′M上时，m的值为 ▲ ．
②当MA′+MC′的值最小时，直接写出m的值．