湖南省衡阳市衡阳县五校联考2023-2024学年九年级上学期第一次月考数学试题

试卷更新日期：2023-11-20 类型：月考试卷

进入出卷网下载

一、选择题（共8小题，满分32分，每小题4分）

1. 若y＝ $\sqrt{x - 3} + \sqrt{6 - 2 x} - 4$ ，则点P（x，y）在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 计算： $(\sqrt{30} + \sqrt{21} - 3) (\sqrt{3} + \sqrt{10} - \sqrt{7})$ 的值等于（　　）

A、 $6 \sqrt{7}$ B、 $- 6 \sqrt{7}$ C、 $20 \sqrt{3} + 6 \sqrt{7}$ D、 $20 \sqrt{3} - 6 \sqrt{7}$

查看试题解析
3. 如图，在甲、乙两个大小不同的6×6的正方形网格中，正方形ABCD，EFGH分别在两个网格上，且各顶点均在网格线的交点上．若正方形ABCD，EFGH的面积相等，甲、乙两个正方形网格的面积分别记为 $S_{甲}$ ， $S_{乙}$ ，有如下三个结论：
①正方形ABCD的面积等于 $S_{甲}$ 的一半；②正方形EFGH的面积等于 $S_{乙}$ 的一半；③ $S_{甲} ： S_{乙} = 9 ： 10$ ．
上述结论中，所有正确结论的序号是（）

A、①② B、②③ C、③ D、①②③

查看试题解析
4. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， D、E分别为 $C A$ 、 $C B$ 的中点， $A F$ 平分 $∠ B A C$ ，交 $D E$ 于点F，若 $A C = 6$ ， $B C = 8$ ，则 $E F$ 的长为（）

A、2 B、1 C、4 D、 $\frac{5}{2}$

查看试题解析
5. 已知一元二次方程a（x+m）²+n＝0（a≠0）的两根分别为﹣3，1，则方程a（x+m﹣2）²+n＝0（a≠0）的两根分别为（　　）

A、1，5 B、﹣1，3 C、﹣3，1 D、﹣1，5

查看试题解析
6. 已知a＞b，则 $\frac{a}{a - b} \sqrt{- \frac{(b - a)^{2}}{a}}$ 的化简结果是（　　）

A、 $\sqrt{a}$ B、 $- \sqrt{a}$ C、 $\sqrt{- a}$ D、 $- \sqrt{- a}$

查看试题解析
7. 已知，在平面直角坐标系中点A、B的坐标分别为A（1，4），B（5，0）．点M、N分别为x轴、y轴上的两个动点．动点P从点A出发以1秒1个单位的速度沿A→N→M到点M，再以1秒 $\sqrt{2}$ 个单位的速度从点M运动到点B后停止．则点P运动花费的时间最短为（　　）秒．

A、5 $\sqrt{2}$ B、4 $\sqrt{2}$ C、5 D、4

查看试题解析
8. 实数a，b，c满足a﹣b+c＝0，则（　　）

A、b²﹣4ac＞0 B、b²﹣4ac＜0 C、b²﹣4ac≥0 D、b²﹣4ac≤0

查看试题解析

二、填空题（共7小题，满分28分，每小题4分）

9. 我们规定运算符号⊗的意义是：当a＞b时，a⊗b＝a+b；当a≤b时，a⊗b＝a﹣b，其它运算符号意义不变．按上述规定，计算 $(\sqrt{3} \otimes \frac{3}{2}) - [(1 - \sqrt{3}) \otimes (- \frac{1}{2})]$ 结果为．

查看试题解析
10. 已知P₁（a﹣1，5）和P₂（2，b﹣1）关于x轴对称，则（a+b）²⁰²²的值为．

查看试题解析
11. 设x₁ ， x₂是一元二次方程x²+x﹣2023＝0的两个根，则 $x_{2}^{1}$ +2x₁+x₂＝．

查看试题解析
12. 如图△ABC中，E、F为BC的三等分点，M为AC的中点，BM与AE、AF分别交于G、H，则BG：GH：HM＝．

查看试题解析
13. 将函数f（x）的图象上每个点的横、纵坐标都乘以﹣1，所得的新函数记作g（x），我们称f（x）与g（x）互为位似函数．则函数y＝3x²﹣1的位似函数是．

查看试题解析
14. 如果方程（x﹣1）（x²﹣2x+ $\frac{k}{4}$ ）＝0的三根可以作为一个三角形的三边之长，那么实数k的取值范围是．

查看试题解析
15. 如图，在正方形ABCD中，点P是AB上一动点（不与A、B重合），对角线AC、BD相交于点O，过点P分别作AC、BD的垂线，分别交AC、BD于点E、F，交AD、BC于点M、N．下列结论：①△APE≌△AME；②PM+PN＝AC；③PE²+PF²＝PO²；④△POF∽△BNF；⑤点O在M、N两点的连线上．其中正确的是．

查看试题解析

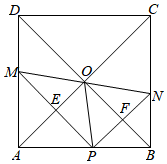
三、解答题（共6小题，满分60分）

16. 已知a＝ $\frac{1}{\sqrt{5} + 2}$ ， b＝ $\frac{1}{\sqrt{5} - 2}$ ．

(1)、求a+b的值；

(2)、设m是a小数部分，n是b整数部分，求代数式4m²+4mn+n²的值．

查看试题解析
17. 接种疫苗是阻断新冠病毒传播的有效途径 $.$ 现有甲、乙两个社区疫苗接种点，已知甲社区接种点平均每天接种疫苗的人数是乙社区接种点平均每天接种疫苗的人数的 $1.25$ 倍，且甲社区接种点完成 $3000$ 人的疫苗接种所需的时间比乙社区接种点完成 $4000$ 人的疫苗接种所需的时间少 $2$ 天．

(1)、求甲、乙两个社区疫苗接种点平均每天接种疫苗的人数；

(2)、一段时间后，乙社区疫苗接种点加大了宣传力度 $.$ 该接种点平均每天接种疫苗的人数比原来平均每天接种疫苗的人数增加了 $25 %$ ，受乙社区疫苗接种点宣传的影响，甲社区疫苗接种点平均每天接种疫苗的人数比原来平均每天接种疫苗的人数减少了 $5 m$ 人，但不低于 $800$ 人，这样乙社区接种点 $(m + 15)$ 天接种疫苗的人数比甲社区接种点 $2 m$ 天接种疫苗的人数多 $6000$ 人，求 $m$ 的值．

查看试题解析
18. 阅读下面的解题过程体会如何发现隐含条件并回答下面的问题
化简： $(\sqrt{1 - 3 x})^{2} - | 1 - x |$ ．
解：隐含条件1﹣3x≥0，解得： $x ⩽ \frac{1}{3}$ ．
∴1﹣x＞0．
∴原式＝（1﹣3x）﹣（1﹣x）＝1﹣3x﹣1+x＝﹣2x．

(1)、【启发应用】
按照上面的解法，试化简 $\sqrt{(x - 3)^{2}} - (\sqrt{2 - x})^{2}$ ．

(2)、【类比迁移】
实数a，b在数轴上的位置如图所示，化简： $\sqrt{a^{2}} + \sqrt{(a + b)^{2}} - | b - a |$ ．

(3)、已知a，b，c为ABC的三边长．化简： $\sqrt{(a + b + c)^{2}} + \sqrt{(a - b - c)^{2}} + \sqrt{(b - a - c)^{2}} + \sqrt{(c - b - a)^{2}}$ ．

查看试题解析
19. 如图（1），在平面直角坐标系中，A（a，0），C（b，2），过C作CB⊥x轴，且满足（a+b）²+ $\sqrt{a - b + 4}$ =0．

(1)、求三角形ABC的面积．

(2)、若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，如图2，求∠AED的度数．

(3)、在y轴上是否存在点P，使得三角形ABC和三角形ACP的面积相等？若存在，求出P点坐标；若不存在，请说明理由．

查看试题解析
20. 阅读材料，根据上述材料解决以下问题：
材料1：若一元二次方程ax²+bx+c＝0（a≠0）的两个根为x₁ ， x₂ ，
则 $x_{1} + x_{2} = - \frac{b}{a} ， x_{1} x_{2} = \frac{c}{a}$
材料2：已知实数m，n满足m²﹣m﹣1＝0，n²﹣n﹣1＝0，且m≠n，求 $\frac{n}{m} + \frac{m}{n}$ 的值．
解：由题知m，n是方程x²﹣x﹣1＝0的两个不相等的实数根，根据材料1得m+n＝1，mn＝﹣1，所以 $\frac{n}{m} + \frac{m}{n} = \frac{m^{2} + n^{2}}{m n} = \frac{(m + n)^{2} - 2 m n}{m n} = \frac{1 + 2}{- 1} = - 3$ ．

(1)、材料理解：一元二次方程5x²+10x﹣1＝0两个根为x₁ ， x₂ ，则：x₁+x₂＝， x₁x₂＝．

(2)、类比探究：已知实数m，n满足7m²﹣7m﹣1＝0，7n²﹣7n﹣1＝0，且m≠n，求m²n+mn²的值．

(3)、思维拓展：已知实数s、t分别满足7s²+7s+1＝0，t²+7t+7＝0，且st≠1．求 $\frac{2 s t + 7 s + 2}{t}$ 的值．

查看试题解析
21. 如图，在正方形ABCD中，边长为4，∠MDN＝90°，将∠MDN绕点D旋转，其中DM边分别与射线BA、直线AC交于E、Q两点，DN边与射线BC交于点F；连接EF，且EF与直线AC交于点P.

(1)、如图1，点E在线段AB上时，①求证：AE＝CF；②求证：DP垂直平分EF；

(2)、当AE＝1时，求PQ的长.

查看试题解析