天津市河西区2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2023-11-20 类型:期中考试
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 在平面直角坐标系中,点(5,-2) 关于原点对称的点的坐标为( )A、(-2, -5) B、(-5, 2) C、(-5, -2) D、(5, -2)2. 在下面4个环保图标中,可以看作是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列结论不正确的是( )A、圆心也是圆的一部分 B、一个圆中最长的弦是直径 C、圆是轴对称图形 D、等弧所在的圆一定是等圆或同圆4. 二次函数的图象如图所示,则( )
3. 下列结论不正确的是( )A、圆心也是圆的一部分 B、一个圆中最长的弦是直径 C、圆是轴对称图形 D、等弧所在的圆一定是等圆或同圆4. 二次函数的图象如图所示,则( ) A、 B、 C、 D、5. 用配方法解一元二次方程。则配方后得到的方程是( )A、 B、 C、 D、6. 将二次函数的图象向上平移3个单位长度,再向左平移6个单位长度,得到的新图象所表示的二次函数为( )A、 B、 C、 D、7. 如图, AB是⊙O 的直径, C是⊙O 上一点. 若则∠A的度数为( )
A、 B、 C、 D、5. 用配方法解一元二次方程。则配方后得到的方程是( )A、 B、 C、 D、6. 将二次函数的图象向上平移3个单位长度,再向左平移6个单位长度,得到的新图象所表示的二次函数为( )A、 B、 C、 D、7. 如图, AB是⊙O 的直径, C是⊙O 上一点. 若则∠A的度数为( )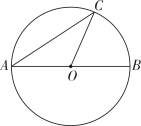 A、30° B、33° C、45° D、60°8. 以原点为中心,把点P(2,3)顺时针旋转90°,得到的点 P′的坐标为( )A、(3, 2) B、(-3, 2) C、(2, -3) D、(-2, -3)9. 抛物线与x轴的两个交点的坐标为( )A、(3, 0) 和(2, 0) B、(-3, 0) 和 (2, 0) C、(2, 0) 和(-1, 0) D、(-2,0) 和(1,0)10. 一个矩形的长比宽多2,面积是80,则矩形的两边长分别为( )A、3和5 B、5和7 C、6和8 D、8和 1011. 如图,在△ABC中, ∠BAC=120°,将△ABC绕点C逆时针旋转得到△DEC, 点A, B的对应点分别为D, E,连接AD. 当点A,D,E在同一条直线上时,下列结论一定正确的是( )
A、30° B、33° C、45° D、60°8. 以原点为中心,把点P(2,3)顺时针旋转90°,得到的点 P′的坐标为( )A、(3, 2) B、(-3, 2) C、(2, -3) D、(-2, -3)9. 抛物线与x轴的两个交点的坐标为( )A、(3, 0) 和(2, 0) B、(-3, 0) 和 (2, 0) C、(2, 0) 和(-1, 0) D、(-2,0) 和(1,0)10. 一个矩形的长比宽多2,面积是80,则矩形的两边长分别为( )A、3和5 B、5和7 C、6和8 D、8和 1011. 如图,在△ABC中, ∠BAC=120°,将△ABC绕点C逆时针旋转得到△DEC, 点A, B的对应点分别为D, E,连接AD. 当点A,D,E在同一条直线上时,下列结论一定正确的是( )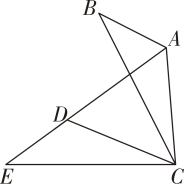 A、∠ABC=∠ADC B、∠DAC=∠E C、AD=AC D、EA=BC12. 九年级一班的同学计划在劳动实践基地内种植蔬菜,班长买回来10米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形,等腰三角形(底边靠墙),半圆形这三种方案,最佳方案是( )
A、∠ABC=∠ADC B、∠DAC=∠E C、AD=AC D、EA=BC12. 九年级一班的同学计划在劳动实践基地内种植蔬菜,班长买回来10米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形,等腰三角形(底边靠墙),半圆形这三种方案,最佳方案是( )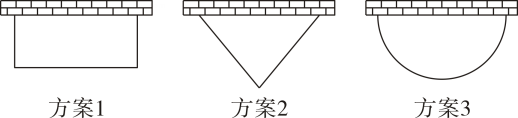 A、方案1 B、方案2 C、方案3 D、三种方案使得菜园面积一样大
A、方案1 B、方案2 C、方案3 D、三种方案使得菜园面积一样大二、填空题(本大题共6小题,每小题3分,共18分)
-
13. 方程的根为.14. 二次函数的顶点坐标为.15. 写出一个没有实数根的一元二次方程.16. 如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,则⊙O 的半径为cm.
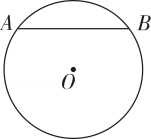 17. 如图,一个圆形纸片⊙O的圆心O与一个正方形的中心重合,已知⊙O的半径和正方形的边长都为4,则圆上任意一点到正方形边上任意一点的距离的最小值为.
17. 如图,一个圆形纸片⊙O的圆心O与一个正方形的中心重合,已知⊙O的半径和正方形的边长都为4,则圆上任意一点到正方形边上任意一点的距离的最小值为.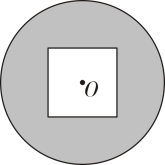 18. 如图,在中, , , 点为的中点,点在上,且 , 将绕点在平面内旋转,点的对应点为点 , 连接 , 当时,的长为 .
18. 如图,在中, , , 点为的中点,点在上,且 , 将绕点在平面内旋转,点的对应点为点 , 连接 , 当时,的长为 .
三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤或推理过程)
-
19.(1)、解方程;(2)、 解方程20. 已知关于x的方程.有两个相等的实数根.(1)、求k的值;(2)、直接写出这两个实数根的两根之和与两根之积.21. 如图, ⊙O 的半径OA 为 10mm,弦AB的长 10mm。
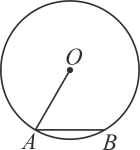 (1)、求∠OAB的度数;(2)、求点O到AB 的距离.22. 已知二次函数(a, b, c 是常数) 的图象过点.点交y轴于点C.(1)、求点C 的坐标和a, b的值;(2)、抛物线的对称轴为.(3)、当时,求y的取值范围.23. 如图,要围一个矩形菜园ABCD,其中一边AD是墙,且AD的长不能超过26m,其余的三边AB、BC、CD用篱笆,且这三边的和为40m .
(1)、求∠OAB的度数;(2)、求点O到AB 的距离.22. 已知二次函数(a, b, c 是常数) 的图象过点.点交y轴于点C.(1)、求点C 的坐标和a, b的值;(2)、抛物线的对称轴为.(3)、当时,求y的取值范围.23. 如图,要围一个矩形菜园ABCD,其中一边AD是墙,且AD的长不能超过26m,其余的三边AB、BC、CD用篱笆,且这三边的和为40m . (1)、AB的长度是否能有两个不同的值都满足菜园面积为说明理由.(2)、当AB的长为多少时,围成的菜园面积最大?24. 在平面直角坐标系中,点A(2,0),点B(2,2).将AB绕点B顺时针旋转,得到A'B,点A旋转后的对应点为记旋转角为α。
(1)、AB的长度是否能有两个不同的值都满足菜园面积为说明理由.(2)、当AB的长为多少时,围成的菜园面积最大?24. 在平面直角坐标系中,点A(2,0),点B(2,2).将AB绕点B顺时针旋转,得到A'B,点A旋转后的对应点为记旋转角为α。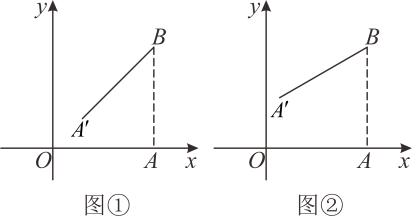 (1)、如图①, 当时,求点的坐标:(2)、如图②, 当时,直接写出点的坐标:(3)、设线段A'B的中点为M,连接OM,求线段OM长的取值范围(直接写出结果即可).25. 在平面直角坐标系xOy中,抛物线与y轴相交于点A,点B与点O是关于点A的对称点. 过点B的直线y=kx+b(其中k<0)与x轴相交于点 C,过点作直线平行于y轴, 是直线上一点,且PB=PC.(1)、填空:点B的坐标为:点C的坐标为 (用含k的式子表示);(2)、求线段PB的长(用含k的式子表示):(3)、点P是否一定在抛物线上? 说明理由.
(1)、如图①, 当时,求点的坐标:(2)、如图②, 当时,直接写出点的坐标:(3)、设线段A'B的中点为M,连接OM,求线段OM长的取值范围(直接写出结果即可).25. 在平面直角坐标系xOy中,抛物线与y轴相交于点A,点B与点O是关于点A的对称点. 过点B的直线y=kx+b(其中k<0)与x轴相交于点 C,过点作直线平行于y轴, 是直线上一点,且PB=PC.(1)、填空:点B的坐标为:点C的坐标为 (用含k的式子表示);(2)、求线段PB的长(用含k的式子表示):(3)、点P是否一定在抛物线上? 说明理由.