北京市海淀区民大附中2023-2024学年八年级上学期数学期中考试试卷
试卷更新日期:2023-11-20 类型:期中考试
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 在平面直角坐标示系中,点关于轴对称的点的坐标是( )A、 B、 C、 D、2. 在下列长度的四根木棒中,能与 , 长的两根木棒钉成一个三角形的是( )A、 B、 C、 D、3. 如图,在中, , 是的边上的中线,那么可以证明≌ , 这里证明全等所使用的判定方法是( )
 A、 B、 C、 D、4. 如图, , 平分交于 , 若 , , 则点到的距离为( )
A、 B、 C、 D、4. 如图, , 平分交于 , 若 , , 则点到的距离为( )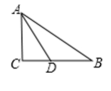 A、 B、 C、 D、不能确定5. 如图所示, , , , , , 则( )
A、 B、 C、 D、不能确定5. 如图所示, , , , , , 则( )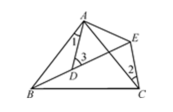 A、 B、 C、 D、无法计算6. 两组邻边分别相等的四边形叫做“筝形”,如图,四边形是一个筝形,其中 , , 在探究筝形的性质时,得到如下结论:
A、 B、 C、 D、无法计算6. 两组邻边分别相等的四边形叫做“筝形”,如图,四边形是一个筝形,其中 , , 在探究筝形的性质时,得到如下结论:
;;≌ ,
其中正确的结论有( )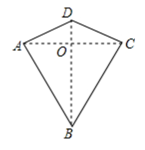 A、个 B、个 C、个 D、个7. 如图,已知与上的点 , 点 , 小临同学现进行如下操作:以点为圆心,长为半径画弧,交于点 , 连接;以点为圆心,长为半径画弧,交于点;以点为圆心,长为半径画弧,交第步中所画的弧于点 , 连接下列结论不能由上述操作结果得出的是( )
A、个 B、个 C、个 D、个7. 如图,已知与上的点 , 点 , 小临同学现进行如下操作:以点为圆心,长为半径画弧,交于点 , 连接;以点为圆心,长为半径画弧,交于点;以点为圆心,长为半径画弧,交第步中所画的弧于点 , 连接下列结论不能由上述操作结果得出的是( )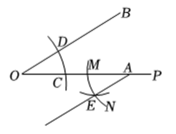 A、 B、 C、 D、8. 如图 , 中, , 为中点,把纸片沿对折得到 , 如图 , 点和点分别为 , 上的动点,把纸片沿折叠,使得点落在的外部,如图所示.设 , 则下列等式成立的是( )
A、 B、 C、 D、8. 如图 , 中, , 为中点,把纸片沿对折得到 , 如图 , 点和点分别为 , 上的动点,把纸片沿折叠,使得点落在的外部,如图所示.设 , 则下列等式成立的是( )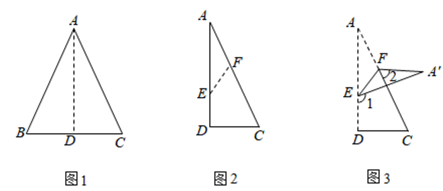 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共8小题,共16.0分)
-
9. 在中, , , 则 .10. 若一个正多边形的每一个外角都等于 , 则这个正多边形的边数为 .11. 等腰三角形的两条边长分别为3和4,则这个等腰三角形的周长是 .12.
由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图1,衣架杆OA=OB=18cm,若衣架收拢时,∠AOB=60°,如图2,则此时A,B两点之间的距离是 cm.
 13. 如图,在中, , , 为中点,则 .
13. 如图,在中, , , 为中点,则 .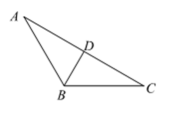 14. 如图,为等边三角形,点在上,点在上, , 与相交于点 , 则 .
14. 如图,为等边三角形,点在上,点在上, , 与相交于点 , 则 .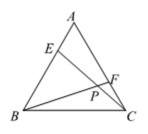 15. 如图,在中, , , 、、三点在一条直线上,且 , 过点作 , 且若 , 则用含的式子表示
15. 如图,在中, , , 、、三点在一条直线上,且 , 过点作 , 且若 , 则用含的式子表示 16. 如图,在平面直角坐标系中,点 , , , 是两个动点,其中点以每秒个单位长度的速度沿折线按照的路线运动,点以每秒个单位长度的速度沿折线按照的路线运动,运动过程中点和同时开始,而且都要运动到各自的终点时停止.设运动时间为秒,直线经过原点 , 且 , 过点 , 分别作的垂线段,垂足为 , , 当与全等时,的值为 .
16. 如图,在平面直角坐标系中,点 , , , 是两个动点,其中点以每秒个单位长度的速度沿折线按照的路线运动,点以每秒个单位长度的速度沿折线按照的路线运动,运动过程中点和同时开始,而且都要运动到各自的终点时停止.设运动时间为秒,直线经过原点 , 且 , 过点 , 分别作的垂线段,垂足为 , , 当与全等时,的值为 .
三、解答题(本大题共8小题,共60.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 已知:如图,是上一点, , , .
求证: .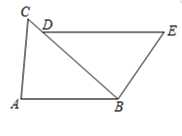 18.
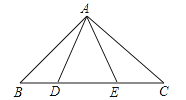
18.如图,点D、E在△ABC的BC边上,AB=AC,AD=AE.求证:BD=CE.
 19. 如图,在平面直角坐标系中,的三个顶点分别是 , , .
19. 如图,在平面直角坐标系中,的三个顶点分别是 , , .
画出关于轴对称的并写出点的坐标; ▲ , ▲
在轴上有一点 , 使得的值最小,请画出图形并直接写出点的坐标: ▲ , ▲20. 如图, , 平分 , 点为中点,求证: .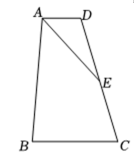 21. 如图,在中, , 于点 , 点为上的一点,且 , 连接并延长交于点 .
21. 如图,在中, , 于点 , 点为上的一点,且 , 连接并延长交于点 .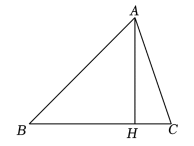 (1)、请补全图形;(2)、写出与的数量关系和位置关系并证明.22. 如图,中, , , 为延长线上一点,点在上,且 .
(1)、请补全图形;(2)、写出与的数量关系和位置关系并证明.22. 如图,中, , , 为延长线上一点,点在上,且 .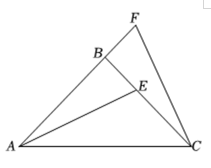 (1)、求证:;
(1)、求证:;
(2)、若 , 求的度数.23. 在中, , , 点在的延长线上,是的中点,是射线上一动点,且 , 连接 , 作 , 交延长线于点 .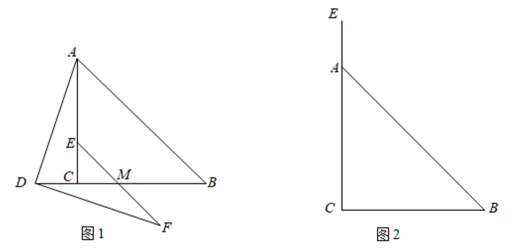 (1)、如图 , 当点在上时,填空: 填“=”、“”或“” .(2)、如图 , 当点在的延长线上时,请根据题意将图形补全,判断与的数量关系,并证明你的结论.24. 小聪和小明两位同学在学习全等三角形时积极思考,提出了以下两个问题:
(1)、如图 , 当点在上时,填空: 填“=”、“”或“” .(2)、如图 , 当点在的延长线上时,请根据题意将图形补全,判断与的数量关系,并证明你的结论.24. 小聪和小明两位同学在学习全等三角形时积极思考,提出了以下两个问题:
问题:如图 , 中, , , 是的角平分线,求:的值.
小聪同学经过思考,发现可以过作于 , 于 , 利用与的面积比来解决这个问题.
问题:如图 , 为等边三角形,点为外一点, , 连接 , 探究 , , 三者之间的数量关系.
小明同学经过思考,发现可以在上截取 , 构造等边三角形 , 从而解决这个问题.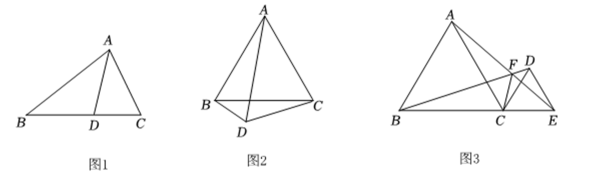 (1)、根据两位同学的思考,完成问题、的解答直接写出结果 .
(1)、根据两位同学的思考,完成问题、的解答直接写出结果 .
(2)、根据问题、的结论,解决下面问题:如图 , 和都是等边三角形,且、、三点共线,连接 , 交于点 , 连接 , 设 , , , 若 , 直接写出的值.