吉林省长春市九台区2023-2024学年八年级上学期阶段性教学质量监测期中数学试题

试卷更新日期：2023-11-20 类型：期中考试

进入 出卷网 下载

一、选择题（本大题共8道题，每题3分，共24分）

  • 1. 4的平方根是（  ）
    A、2 B、±2 C、±2 D、-2

    查看试题解析

  • 2. 在5 ， -1.6，0，2这四个数中，最大的数是（ ）
    A、5 B、-1.6 C、0 D、2

    查看试题解析

  • 3. 下列计算正确的是（ ）
    A、（a2）3=a5 B、（2a2）2=2a4 C、a3·a4=a7 D、a4÷a=a4

    查看试题解析

  • 4. 下列各数中，为无理数的是（ ）
    A、38 B、4 C、13 D、2

    查看试题解析

  • 5. 下列等式中，从左到右的变形是因式分解的是（ ）
    A、x（x-1）=x2-x B、（x+1）2=x2 +2x+1 C、x2-1=（x+1）（x-1） D、x+1= x（1+1x）

    查看试题解析

  • 6. 下列命题中是假命题的是（  ）
    A、对顶角相等 B、两直线平行，同旁内角互补 C、同位角相等 D、三角形的内角和是180°

    查看试题解析

  • 7. 如图，工人师傅设计了一种测零件内径AB的卡钳，卡钳交叉点O为AA'、BB'的中点，只要量出A'B'的长度，就可以知道该零件内径AB的长度．依据的数学基本事实是（  ）

    A、两边及其夹角分别相等的两个三角形全等 B、两点确定一条直线 C、两角及其夹边分别相等的两个三角形全等 D、两点之间线段最短

    查看试题解析

  • 8. 如图，根据计算长方形ABCD的面积，可以说明下列哪个等式成立（  ）

    A、（a+b）2=a2+2ab+b2 B、（a-b）2=a2-2ab+b2 C、（a+b）（a-b）=a2-b2 D、a（a+b）=a2+ab

    查看试题解析

二、填空题（本大题共6道题，每题3分，共18分）

三、解答题（本大题共10道题，共78分）

  • 15. 计算：
    (1)、a3·a+（-a2）3÷a2
    (2)、（9a5-15a3+ 6a）÷3a

    查看试题解析

  • 16. 分解因式：
    (1)、-a3+2a2-a
    (2)、（2m+n）-（m+n）2

    查看试题解析

  • 17. 已知x2-x+1=0，求代数式（x+1）2-（x+1）（2x-1）的值．

    查看试题解析

  • 18. 已知x-1的算术平方根是3，x-2y+1的立方根是3，求x2-y2的平方根．

    查看试题解析

  • 19. 如图，在△ABC和△ADE中，延长BC交DE于F．∠B=∠D，AC=AE，∠ACF+∠AED=180°，求证： AB=AD

    查看试题解析

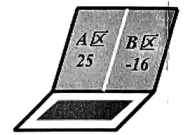
  • 20. 如图，所有的网格都是由边长为1的小正方形构成，每个小正方形的顶点称为格点，顶点都是格点的三角形称为格点三角形，△ABC为格点三角形．图1，图2，图3都是6X6的正方形网格，点M，点N都是格点，请分别按要求在网格中作格点三角形：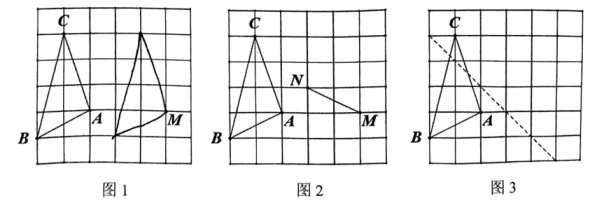

    (1)、在图1中作△MDE，使△MDE是由△ABC经过平移而得到的全等图形；
    (2)、在图2中作△MNP，使它与△ABC全等（利用“边边边”） ；
    (3)、在图3中作△ONFG，使△NFG是由△ABC沿所给虚线翻折而得到的全等图形；

    查看试题解析

  • 21. 有一电脑程序：每按一次按键，屏幕的A区就会自动加上a2 ， 同时B区会自动减去3a，且均显示化简后的结果．已知A， B两区初始显示的分别是25和-16，如图．例如：第一次按键后，A，B两区分别显示：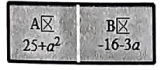

    (1)、从初始状态按2次后，分别求A，B两区显示的结果；
    (2)、从初始状态按4次后，计算A， B两区代数式的和，请判断这个和能为负数吗？说明理由．

    查看试题解析

  • 22.   
    (1)、 你能求出（a-1）（a99 +a98 +a97 +……+a2 +a+ 1）的值吗？遇到这样的问题，我们可以先从简单的情况入手，分别计算下列各式的值．

    （a-1）（a+1）=； （a-1）（a2 +a+1）=

    （a-1）（a3+a2+a+1）=；

    由此我们可以得到： （a-1）（a99+a98+……+a+1）=

    (2)、利用（1）的结论，计算： 22023 +22022+22021 +……+22 +2+1

    查看试题解析

  • 23. 完全平方公式经过适当的变形，可以解决很多数学问题．

    例如：若a+b=3，ab=1，求a2+b2的值．

    解：∵a+b=3，ab=1，

    ∴（a+b）2=9，2ab=2．

    ∴a2 +b2 +2ab=9，

    ∴a2+b2=7．

    根据上面的解题思路与方法解决下列问题：

    (1)、若m+n=3，mn=1，则（m-n）2= ；
    (2)、如图，C是线段AB上的一点，分别以AC，BC为边向两侧作正方形BCFG与正方形ACDE，设AB=6，两正方形的面积和为20，求△AFC的面积．

    查看试题解析

  • 24. 如图，Rt△AEO≌Rt△BEC，延长AO交BC于D，BD：DC=2：3，AO=5，解决下列问题：

    (1)、BD= ， AD与BC的位置关系是；
    (2)、动点P从点O出发，沿线段OA以每秒1个单位长度的速度向终点A运动，动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动．P，Q两点同时出发，当点P到达A点时，P，Q两点同时停止运动．设点P的运动时间为1秒，△AOQ的面积为S，请用含t的式子表示S，并直接写出相应的t的取值范围；
    (3)、在（2）的条件下，点F是直线AC上的一点，且CF=BO，是否存在t值，

    使以点B，O，P为顶点的三角形与以点F，C，Q为顶点的三角形全等？若存在，请直接写出符合条件的t值；若不存在，请说明理由．

    查看试题解析