吉林省松原市乾安县2023-2024学年八年级上学期期中数学试题

试卷更新日期：2023-11-20 类型：期中考试

进入出卷网下载

一、选择题（本大题共6小题，每小题2分，共12分）

1. 已知三角形的两边长分别为3、7，则第三边a的取值范围是（　　）

A、 $4 < a < 10$ B、 $4 \leq a \leq 10$ C、 $a > 4$ D、 $a < 10$

查看试题解析
2. 从一个多边形的任何一个顶点出发都只有2条对角线，则它的边数是（）条.

A、3 B、4 C、5 D、6

查看试题解析
3. 下面四种化学仪器的示意图是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 等腰三角形的一条边长为6，另一边长为14，则它的周长为（　　）

A、26 B、26或34 C、34 D、20

查看试题解析
5. 如图，小明书上的三角形被墨迹污染了一部分，他根据所学的知识很快就画出了一个与书上完全一样的三角形，那么小明画图的依据是（）

A、ASA B、AAS C、SAS D、SSS

查看试题解析
6. 下列各图中，OP 是∠MON 的平分线，点E，F，G 分别在射线OM，ON，OP 上，则可以解释定理“角的平分线上的点到角的两边的距离相等”的图形是（）

A、 B、 C、 D、

查看试题解析

二、填空题（本大题共8小题，每小题3分，共24分）

7. 若正n边形的一个外角为 $72 °$ ，则 $n =$ ．

查看试题解析
8.
如图，在建筑工地上，工人师傅砌门时，常用木条EF固定长方形门框，使其不变形，这种做法的根据是．

查看试题解析
9. 如图，已知 $A D$ 与 $B C$ 交于 $O$ 点， $O A = O B$ ，要使 $△ A O C ≌ △ B O D$ ，添加一个你认为合适的条件为．

查看试题解析
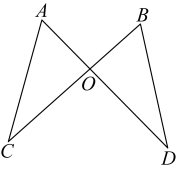10. 如图，小亮从A点出发，沿直线前进10米后向左转30°，再沿直线前进10米，又向左转30°，……照这样走下去，他第一次回到出发地A点时，一共走了米。

查看试题解析
11. 如图，用圆规以直角顶点O为圆心，以适当半径画一条弧交两直角边于A，B两点，若再以A点为圆心，以OA为半径画弧，与弧AB交于点C，则∠BOC等于．

查看试题解析
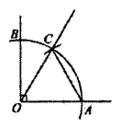12. 两把相同的长方形直尺按如图所示方式摆放，记两把直尺的接触点为P ，其中一把直尺边缘和射线 $O A$ 重合，另一把直尺的下边缘与射线 $O B$ 重合，连接 $O P$ 并延长，若 $∠ B O P = 28 °$ ，则 $∠ A O B$ 的度数为．

查看试题解析
13. 如图， $△ A B C$ 的面积是 $150 c m^{2}$ ，最长边 $A B = 30 c m$ ， $A D$ 平分 $∠ B A C$ ，点M ， N分别是 $A D$ ， $A C$ 上的动点，则 $C M + M N$ 的最小值为 $c m$ ．

查看试题解析
14. 如图， $A D$ 是 $△ A B C$ 的角平分线， $D E$ 、 $D F$ 分别是 $△ A B D$ 和 $△ A C D$ 的高，则下列结论：
① $E F$ 垂直平分 $A D$ ；② $A D ⊥ E F$ ；③ $A E + D F = A F + D E$ ；④ $O$ 为 $E F$ 的中点．其中一定正确的是（填序号）

查看试题解析

三、解答题（每小题5分，共20分）

15. 已知一个多边形的内角和为 $1080 °$ ，求这个多边形的边数．

查看试题解析
16. 如图，在 $△ A B C$ 中， $∠ C = 30 °$ ， $∠ B = 58 °$ ， $A D$ 平分 $∠ C A B$ 交 $B C$ 于 $D$ ．求 $∠ C A D$ 和 $∠ 1$ 的度数．

查看试题解析
17. 如图，点 $C 、 E 、 B 、 F$ 在一条直线上， $A B ⊥ C F$ 于 $B$ ， $D E ⊥ C F$ 于 $E ， A C = D F ， A B = D E$ ．求证： $B C = E F$ ．

查看试题解析
18. 小明利用一根长 $3 m$ 的竿子 $C D$ 来测量路灯杆 $A B$ 的高度，方法如下：如图，在地面上选一点P ，使 $B P = 3 m$ ，并测得 $∠ A P B = 70 °$ ，然后把 $C D$ 在 $B P$ 的延长线上左右移动，使 $C D ∥ A B$ ，且 $∠ C P A = 90 °$ ，此时测得 $B D = 11.2 m$ ．

(1)、此时 $∠ C$ 度数为；

(2)、路灯杆 $A B$ 的高度为m．

查看试题解析

四、解答题（每小题7分，共28分）

19.
⑴如图1，在正方形网格中，点A、B、C在小正方形的顶点上．在图1中作出与 $△ A B C$ 关于直线 $l$ 对称的 $△ A B^{'} C^{'}$ ；
⑵在图2中求作 $∠ C A B$ 的角平分线，交 $B C$ 于点D（尺规作图，保留作图痕迹）．

查看试题解析
20. 已知：如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A D$ 是 $△ A B C$ 的角平分线， $D E ⊥ A B$ ，垂足为点 $E$ ， $A E = B E$ ．

(1)、求 $∠ B$ 的度数．

(2)、如果 $A C = 3$ cm， $C D = 2$ cm，求 $△ A B D$ 的面积．

查看试题解析
21. 已知：在 $Δ A B C$ 中， $A B = A C$ ， $D$ 为 $A C$ 的中点， $D E ⊥ A B$ ， $D F ⊥ B C$ ，垂足分别为点 $E ， F$ ，且 $D E = D F$ .求证： $Δ A B C$ 是等边三角形.

查看试题解析
22. 已知a、b、c是△ABC的三边长，a=4，b=6，设三角形的周长是x．

(1)、直接写出c及x的取值范围；

(2)、若x是小于18的偶数，①求c的长；
②判断△ABC的形状．

查看试题解析

五、解答题（每小题8分，共16分）

23. 如图，在折纸活动中，小李制作了一张△ABC的纸片，点D，E分别在边AB，AC上，将△ABC沿着DE折叠压平，A与A'重合.

(1)、若∠B＝50°，∠C＝60°，求∠A的度数；

(2)、若∠1+∠2＝130°，求∠A的度数.

查看试题解析
24. 如图，在等边三角形 $A B C$ 中，点E在 $A B$ 上，点D在 $C B$ 的延长线上，且 $A E = B D$ ．

(1)、当点E为 $A B$ 的中点时，如图1，求证： $E C = E D$ ；

(2)、当点E不是 $A B$ 的中点时，如图2， $E C$ 与 $E D$ 还相等吗？请说明理由．

查看试题解析

六、解答题（每小题10分，共20分）

25. 综合与实践
数学模型可以用来解决一类问题，是数学应用的基本途径．通过探究图形的变化规律，再结合其他数学知识的内在联系，最终可以获得宝贵的数学经验，并将其运用到更广阔的数学天地．

(1)、发现问题：如图1，在 $△ A B C$ 和 $△ A E F$ 中， $A B = A C$ ， $A E = A F$ ， $∠ B A C = ∠ E A F = 30 °$ ，连接 $B E$ ， $C F$ ，延长 $B E$ 交 $C F$ 于点 $D$ ．则 $B E$ 与 $C F$ 的数量关系：， $∠ B D C =$ $°$ ；

(2)、类比探究：如图2，在 $△ A B C$ 和 $△ A E F$ 中， $A B = A C$ ， $A E = A F$ ， $∠ B A C = ∠ E A F = 120 °$ ，连接 $B E$ ， $C F$ ，延长 $B E$ ， $F C$ 交于点 $D$ ．请猜想 $B E$ 与 $C F$ 的数量关系及 $∠ B D C$ 的度数，并说明理由．

查看试题解析
26. 如图，已知 $△ A B C$ 中， $A B = A C = 12 c m$ ， $B C = 10 c m$ ，点D为 $A B$ 的中点．如果点P在线段 $B C$ 上以 $2 c m / s$ 的速度由点B向点C运动，同时，点Q在线段 $A C$ 上由点A向点C以 $4 c m / s$ 的速度运动．若P ， Q两点分别从B ， A两点同时出发，回答下列问题：

(1)、经过 $2 s$ 后，此时 $P B =$ $c m$ ， $C Q =$ $c m$ ；

(2)、在（1）的条件下，证明： $△ B P D ≌ △ C Q P$ ；

(3)、求经过多少秒后， $△ C P Q$ 为等腰三角形且周长为 $18 c m$ ?

查看试题解析