四川省泸州市龙马潭区2023-2024学年七年级上学期期中数学试题

试卷更新日期：2023-11-20 类型：期中考试

进入出卷网下载

一、选择题（本题共12小题，每小题3分，共36分，每小题只有一个选项是符合题意的）

1. －2023的绝对值是（）

A、－2023 B、 $\frac{1}{2023}$ C、 $- \frac{1}{2023}$ D、2023

查看试题解析
2. 2022年3月23日，“天宫课堂”再度开课，三位“太空教师”翟志刚、王亚平、叶光富在距离地球约400000米的中国空间站为广大青少年带来了一场精彩的太空科普课，数字400000用科学记数法表示为（）

A、 $0.4 \times 1 0^{6}$ B、 $4 \times 1 0^{6}$ C、 $0.4 \times 1 0^{5}$ D、 $4 \times 1 0^{5}$

查看试题解析
3. 下列说法中，正确的是（　　）

A、正整数和负整数统称整数 B、整数和分数统称有理数 C、零既可以是正整数，也可以是负整数 D、一个有理数不是正数就是负数

查看试题解析
4. 下列关于单项式 $- \frac{7 π x^{3} y}{6}$ 的说法中，正确的是（）

A、系数是 $- \frac{7}{6}$ ，次数是5 B、系数是 $- \frac{7 π}{6}$ ，次数是5 C、系数是 $- \frac{7 π}{6}$ ，次数是4 D、系数是 $- \frac{7}{6}$ ，次数是4

查看试题解析
5. 下列各组数中是同类项的是（）

A、4x和4y B、 $4 x y^{2}$ 和 $4 x y$ C、 $4 x y^{2}$ 和 $- 8 x^{2} y$ D、 $- 4 x y^{2}$ 和 $4 y^{2} x$

查看试题解析
6. 下列运算正确的是（）

A、 $- 2^{2} = 4$ B、 ${(- 2 \frac{1}{3})}^{3} = - 8 \frac{1}{27}$ C、 ${(- \frac{1}{2})}^{3} = - \frac{1}{8}$ D、 $(- 2)^{3} = - 6$

查看试题解析
7. 下列说法正确的是（）

A、如果 $a > b$ ，那么 $a^{2} > b^{2}$ B、如果 $a^{2} > b^{2}$ ，那么 $a > b$ C、如果 $| a | > | b |$ ，那么 $a^{2} > b^{2}$ D、如果 $a > b$ ，那么 $| a | > | b |$

查看试题解析
8. 比较 $(- 2)^{3}$ 和 $- 2^{3}$ ，下列说法正确的是（）

A、它们底数相同，指数也相同 B、它们底数相同，但指数不相同 C、 $(- 2)^{3} > - 2^{3}$ D、 $(- 2)^{3} = - 2^{3}$

查看试题解析
9. 下列各式去括号正确的是（）

A、 $- (a - 3 b) = - a - 3 b$ B、 $a + (5 a - 3 b) = a + 5 a - 3 b$ C、 $- 2 (x - y) = - 2 x - 2 y$ D、 $- y + 3 (y - 2 x) = - y + 3 y - 2 x$

查看试题解析
10. 多项式 $2 x^{3} - 8 x^{2} + x - 1$ 与多项式 $3 x^{3} + 2 m x^{2} - 5 x + 3$ 的和不含二次项，则m等于（）

A、2 B、－2 C、4 D、－4

查看试题解析
11. 如图，数轴上P ， Q ， S ， T四点表示的整数分别是p ， q ， s ， t ，且有 $p + q + s + t = - 2$ （数轴上每1小格为1个单位长度），则原点应是点（）

A、P B、Q C、S D、T

查看试题解析
12. 已知整数 $a_{1} ， a_{2} ， a_{3} ， a_{4} ， \cdot \cdot \cdot$ 满足下列条件： $a_{1} = 0 ， a_{2} = - | a_{1} + 1 | ， a_{3} = - | a_{2} + 2 | ， a_{4} = - | a_{3} + 3 |$ ， ……依此类推，则 $a_{2017}$ 的值为（）

A、－1009 B、－1008 C、－2017 D、－2016

查看试题解析

二、填空题（每小题3分，共18分）

13. 计算：|-3|-1= ．

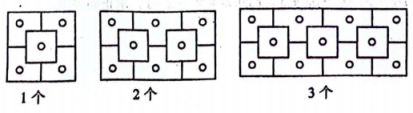
查看试题解析
14. 已知x＋y＝3，则代数式2x＋2y－1的值是．

查看试题解析
15. 在数轴上，与表示5的点距离为4的点所表示的数是．

查看试题解析
16. 规定一种新运算： $a Δ b = a \cdot b - a - b + 1$ ，如： $3 Δ 4 = 3 \times 4 - 3 - 4 + 1$ ，请比较大小： $(- 3) Δ 4$ $4 Δ (- 3)$ （填“＜”、“＝”或“＞”）．

查看试题解析
17. 如果a、b互为倒数，c、d互为相反数，且m＝－1，则代数式 $2 a b - (c + d) + m^{2} =$ ．

查看试题解析
18. 下列图案是晋商大院窗格的一部分，其中“○”代表窗纸上所贴的剪纸：
用代数式表示第n个图中所贴剪纸“○”的个数．

查看试题解析

三、解答题（共8个小题，共66分）

19. 计算：

(1)、 $3 + (- 1) - (- 3) + 2$

(2)、 $12 + | - 6 | - (- 8) \times 3$

(3)、 $(\frac{2}{3} - \frac{1}{4} - \frac{3}{8}) \times 24$

(4)、 $- 1^{2021} - [- 3 \times (2 \div 3)^{2} - \frac{4}{3} \div 2^{2}]$

查看试题解析
20.

(1)、化简： $x - (2 x - y) + (3 x - 2 y)$ ．

(2)、先化简，再求值 $2 x y + (- 3 x^{3} + 5 x y + 2) - 3 (2 x y - x^{3} + 1)$ ，其中 $x = - \frac{2}{3} ， y = \frac{3}{2}$ ．

查看试题解析
21. 某人用400元购买了8套儿童服装，准备以一定的价格出售，如果每套儿童服装以55元的价格为标准，超出的记作正数，不足的记作负数，记录如下（单位：元）：＋2，－3，＋2，＋1，－2，－1，0，－2.当他卖完这8套儿童服装后是盈利还是亏损？盈利（或亏损）多少？

查看试题解析
22. 有理数a ， b ， c在数轴上的位置如图所示．

(1)、由图可得：a－c0，a－b0，b－c0（填＜，＞，＝）；

(2)、结合（1）化简： $| a - c | + | a - b | - | b - c |$ ．

查看试题解析
23. 如图所示，某长方形广场的四角都有一块半径相同的扇形草地，若扇形的半径为r米，长方形长为a米，宽为b米．

(1)、请用代数式表示空地的面积；

(2)、若长方形长为300米，宽为200米，扇形的半径为10米，求广场空地的面积（计算结果保留 $π$ ）．

查看试题解析
24. 某位同学做一道题：已知两个多项式A、B ，求A＋2B的值．他误将A＋2B看成 $2 A + B$ ，求得结果为 $3 x^{2} - 3 x + 5$ ，已知 $B = x^{2} - x - 1$ ，求正确答案：

查看试题解析
25. 观察下面的变形规律：
$\frac{1}{1 \times 3} = \frac{1}{2} \times (1 - \frac{1}{3})$
$\frac{1}{3 \times 5} = \frac{1}{2} \times (\frac{1}{3} - \frac{1}{5})$
$\frac{1}{5 \times 7} = \frac{1}{2} \times (\frac{1}{5} - \frac{1}{7})$
……
解答下面的问题：

(1)、第5个式子为；

(2)、若n为奇数正整数，请你猜想 $\frac{1}{n (n + 2)} =$ ；

(3)、根据你得到的启示，试解答下题：若有理数a ， b满足 $| a - 1 | + {(b - 3)}^{2} = 0$ ，求 $\frac{1}{a b} + \frac{1}{(a + 2) (b + 2)} + \frac{1}{(a + 4) (b + 4)} + \cdot \cdot \cdot + \frac{1}{(a + 100) (b + 100)}$ 的值．

查看试题解析
26. 如果A、B两点在数轴上分别表示有理数a、b ，那么它们之间的距离 $A B = | a - b |$ ．如图1，已知数轴上两点A、B对应的数分别为－3和8，数轴上另有一个点P对应的数为x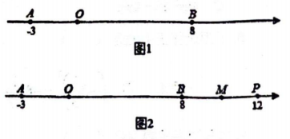

(1)、点P、B之间的距离 $P B =$ ．

(2)、若点P在A、B之间，则 $| x + 3 | + | x - 8 | =$ ．

(3)、①如图2，若点P在点B右侧，且 $x = 12$ ，取BP的中点M ，试求2AM－AP的值．
②若点P为点B右侧的一个动点，取BP的中点M ，那么2AM－AP是定值吗？如果是，请求出这个定值；如果不是，请说明理由．

查看试题解析