(人教版)2024年中考数学一轮复习 数与式--代数式 练习题
试卷更新日期:2023-11-18 类型:一轮复习
一、选择题
-
1. 定义一种新运算: , 如 , 则的结果为( )A、 B、 C、 D、2. 某校举办的知识竞赛,共道题,规定答对一道题加x分,答错一道题(不答按错)扣分,小明答错了2道题,他得到的分数是( )A、 B、 C、 D、3. 在下列各式中,不是代数式的是( )A、7 B、 C、 D、4. 式子可以化为( )A、 B、 C、 D、5. 已知m = 2,则代数式2m-1 的值为( )A、1 B、﹣1 C、3 D、﹣36. 小华总结了以下结论,其中一定成立的是( )A、0不是单项式 B、多项式是二次三项式 C、“a与b的和的平方”表示为 D、“x的一半与y的2倍的差是非负数”表示为7. 如图所示的运算程序中,甲输入的x为 , 乙输入的x为 , 丙输入的x为 . 若 , 则输出结果相同的是( )
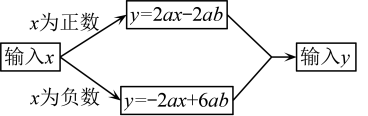 A、甲和乙 B、甲和丙 C、乙和丙 D、三人均不相同8. 观察下列关于x的单项式: , , , , …按照上述规律,则第2022个单项式是( )A、 B、 C、 D、9. 已知抛物线与x轴的一个交点为 , 则代数式的值为( )A、2020 B、2021 C、2022 D、202310. 已知a+b=4,则代数式1+ + 的值为( )A、3 B、1 C、0 D、﹣1
A、甲和乙 B、甲和丙 C、乙和丙 D、三人均不相同8. 观察下列关于x的单项式: , , , , …按照上述规律,则第2022个单项式是( )A、 B、 C、 D、9. 已知抛物线与x轴的一个交点为 , 则代数式的值为( )A、2020 B、2021 C、2022 D、202310. 已知a+b=4,则代数式1+ + 的值为( )A、3 B、1 C、0 D、﹣1二、填空题
-
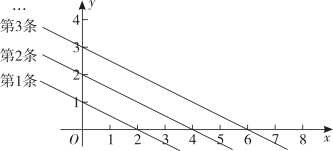
11. 若 , 则的值是 .12. 如图是平面直角坐标系中的一组直线,按此规律推断,第5条直线与x轴交点的横坐标是.
 13. 若圆柱的底面半径和高均为a,则它的体积是(用含a的代数式表示).14. 在平面直角坐标系中,已知点与点关于轴对称,则 .15. 如图是某种杆秤.在秤杆的点处固定提纽,点处挂秤盘,点为0刻度点.当秤盘不放物品时,提起提纽,秤砣所挂位置移动到点 , 秤杆处于平衡.秤盘放入克物品后移动秤砣,当秤砣所挂位置与提扭的距离为毫米时秤杆处于平衡.测得与的几组对应数据如下表:
13. 若圆柱的底面半径和高均为a,则它的体积是(用含a的代数式表示).14. 在平面直角坐标系中,已知点与点关于轴对称,则 .15. 如图是某种杆秤.在秤杆的点处固定提纽,点处挂秤盘,点为0刻度点.当秤盘不放物品时,提起提纽,秤砣所挂位置移动到点 , 秤杆处于平衡.秤盘放入克物品后移动秤砣,当秤砣所挂位置与提扭的距离为毫米时秤杆处于平衡.测得与的几组对应数据如下表:/克
0
2
4
6
10
/毫米
10
14
18
22
30
由表中数据的规律可知,当克时,毫米.

三、解答题
-
16. 定义一种新运算: , 例如2(-3) =(1)、求的值(2)、解方程: .17. 解答
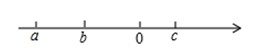 (1)、已知的平方根是 , 的立方根是 , 是的整数部分,求的算术平方根.
(1)、已知的平方根是 , 的立方根是 , 是的整数部分,求的算术平方根.
(2)、已知实数 , , 在数轴上的对应点如图所示,化简 .18. 先观察下列等式,再回答问题:①;
②;
③;
(1)、请根据上面三个等式提供的信息,猜想:=;(2)、请按照上面各等式的规律,计算的值.19. 某木工师傅制作如图的一个工件(阴影部分). (1)、用含a,b的式子表示阴影部分的面积;(2)、当a=4厘米,b=10厘米时,求阴影部分图形的面积(结果用含π的式子表示)
(1)、用含a,b的式子表示阴影部分的面积;(2)、当a=4厘米,b=10厘米时,求阴影部分图形的面积(结果用含π的式子表示)四、综合题
-
20. 某校为实现垃圾分类投放,计划购进大小两种垃圾桶,大小垃圾桶的进价分别为m元/个、50元/个,购进7个大垃圾桶和10个小垃圾桶.(1)、用含m的代数式表示共付款多少元?(2)、若 , 学校预算购买垃圾桶资金为1200元是否够用?为什么?21. 如图小明家有一块长8米,宽6米的长方形花园,为便于管理,计划修建两条同样宽的道路(图中阴影部分,两条路均与长方形的边垂直),余下部分种花.
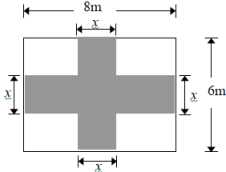 (1)、若道路的宽为x米,用代数式表示种花部分的面积;(2)、当时,种花部分的面积是多少?22. 新定义探究应用:用“”“”定义两种新运算:对于两个数 , , 规定 , 例如:; .(1)、求的值;(2)、求的值;(3)、当为何值时,的值与的值相等.23. 在数轴上有A , B两点,点B表示的数为b . 对点A给出如下定义:当时,将点A向右移动2个单位长度,得到点P;当时,将点A向左移动个单位长度,得到点P . 称点P为点A关于点B的“联动点”.如图,点A表示的数为-1.
(1)、若道路的宽为x米,用代数式表示种花部分的面积;(2)、当时,种花部分的面积是多少?22. 新定义探究应用:用“”“”定义两种新运算:对于两个数 , , 规定 , 例如:; .(1)、求的值;(2)、求的值;(3)、当为何值时,的值与的值相等.23. 在数轴上有A , B两点,点B表示的数为b . 对点A给出如下定义:当时,将点A向右移动2个单位长度,得到点P;当时,将点A向左移动个单位长度,得到点P . 称点P为点A关于点B的“联动点”.如图,点A表示的数为-1. (1)、在图中画出当时,点A关于点B的“联动点”P;(2)、点A从数轴上表示-1的位置出发,以每秒1个单位的速度向右运动.点B从数轴上表示7的位置同时出发,以相同的速度向左运动,两个点运动的时间为t秒.
(1)、在图中画出当时,点A关于点B的“联动点”P;(2)、点A从数轴上表示-1的位置出发,以每秒1个单位的速度向右运动.点B从数轴上表示7的位置同时出发,以相同的速度向左运动,两个点运动的时间为t秒.①点B表示的数为 ▲ (用含t的式子表示);
②是否存在t , 使得此时点A关于点B的“联动点”P恰好与原点重合?若存在,请求出t的值;若不存在,请说明理由.