2023-2024学年北师大版数学八年级上册 7.4平行线的性质 同步练习(培优卷)
试卷更新日期:2023-11-18 类型:同步测试
一、选择题
-
1. 有下列命题:
①两条直线被第三条直线所截,同位角相等;②过一点有且只有一条直线与已知直线垂直;③算术平方根等于它本身的数是1;④如果点P(3-2n,1)到两坐标轴的距离相等,则n=1;⑤若a2=b2 , 则a=b;⑥若 , 则a=b.其中假命题的个数是( )
A、1个 B、3个 C、5个 D、6个2. 如图,直线AB∥CD,直线EF分别与AB, ,CD交于点E, F,EG平分∠BEF,交CD于点G, 若∠1=55°, 则∠2的度数为( ) A、117.5° B、110° C、118.5° D、125°3. 如图,在四边形ABCD中, , 若∠DAB的角平分线AE交CD于E,连结BE,且BE平分∠ABC,则以下命题不正确的是( )
A、117.5° B、110° C、118.5° D、125°3. 如图,在四边形ABCD中, , 若∠DAB的角平分线AE交CD于E,连结BE,且BE平分∠ABC,则以下命题不正确的是( ) A、 B、E为CD中点 C、 D、4. 如图,直线EF∥MN,将一块含45°角的直角三角板(∠C=90°)如图摆放,∠CQM=66°,则∠AHE的度数是( )
A、 B、E为CD中点 C、 D、4. 如图,直线EF∥MN,将一块含45°角的直角三角板(∠C=90°)如图摆放,∠CQM=66°,则∠AHE的度数是( ) A、120° B、118° C、115° D、111°5. 如图,已知 , , 那么添加下列一个条件后,能判定≌的是( )
A、120° B、118° C、115° D、111°5. 如图,已知 , , 那么添加下列一个条件后,能判定≌的是( )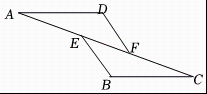 A、 B、 C、 D、6. 如图,在五边形中, , , , 则的度数是( )
A、 B、 C、 D、6. 如图,在五边形中, , , , 则的度数是( ) A、 B、 C、 D、7. 如图, , 平分 , , , , 则下列结论:
A、 B、 C、 D、7. 如图, , 平分 , , , , 则下列结论:
;平分;; .
其中正确结论的个数是( )
A、个 B、个 C、个 D、个8. 如图,把长方形ABCD沿EF折叠后,点D , C'的位置.若∠D'EF=65°,则∠C′FB是( ) A、45° B、50° C、60° D、65°9. 如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:
A、45° B、50° C、60° D、65°9. 如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:①∠AOE=65°;②OF平分∠BOD;③∠GOE=∠DOF;④∠AOE=∠GOD.
其中正确结论的个数是( )
 A、1个 B、2个 C、3个 D、4个10. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,则回答正确的是( )
A、1个 B、2个 C、3个 D、4个10. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,则回答正确的是( )已知:如图, , , 垂足为D , F , .
求证: .
证明:∵ , ,
∴ ◎ ,
∴(同位角相等,两直线平行),
∴ @ (两直线平行,同旁内角互补).
又∵ ,
∴ ▲ (同角的补角相等),
∴( ※ 相等,两直线平行).
 A、◎代表 B、@代表 C、▲代表 D、※代表同位角
A、◎代表 B、@代表 C、▲代表 D、※代表同位角二、填空题
-
11. 如图,一副直角三角板中, , , , 现将直角顶点按照如图方式叠放,点在直线上方,且 , 能使三角形有一条边与平行的所有的度数为 .
 12. 如图,将一张长方形纸片沿折叠后,点、分别落在点、的位置,的延长线与相交于点 , 若 , 则
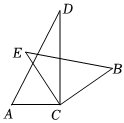
12. 如图,将一张长方形纸片沿折叠后,点、分别落在点、的位置,的延长线与相交于点 , 若 , 则 13. 将一副三角板中的两块直角三角尺的直角顶点 C 按如图方式叠放在一起,其中∠A=60°,∠D=30°,∠E=∠B=45°.当∠ACE<90°,且点 E 在直线 AC 的上 方时,若这两块三角尺有两条边平行,则∠ACE= .
13. 将一副三角板中的两块直角三角尺的直角顶点 C 按如图方式叠放在一起,其中∠A=60°,∠D=30°,∠E=∠B=45°.当∠ACE<90°,且点 E 在直线 AC 的上 方时,若这两块三角尺有两条边平行,则∠ACE= . 14. 如图, , 在的两边上分别过点A和点C向同方向作射线和 , 且 , 若和的角平分线所在的直线交于点P(P与C不重合),则的大小为 .
14. 如图, , 在的两边上分别过点A和点C向同方向作射线和 , 且 , 若和的角平分线所在的直线交于点P(P与C不重合),则的大小为 .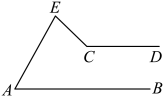 15. 某街道要修建一条管道,如图,管道从A站沿北偏东方向到B站,从B站沿北偏西方向到C站,为了保持水管与方向一致,则为°.
15. 某街道要修建一条管道,如图,管道从A站沿北偏东方向到B站,从B站沿北偏西方向到C站,为了保持水管与方向一致,则为°.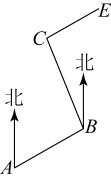
三、综合题
-
16. 如图,在四边形中, , 的平分线交的延长线于点E,F是的中点,连接并延长交于点G.
 (1)、求证:;(2)、若 , , 求的度数.17. 已知:直线 , 经过直线上的定点的直线交于点 , 点 , 为直线上的两点,且点在点右侧,点的左侧时,连接 , , 满足 .
(1)、求证:;(2)、若 , , 求的度数.17. 已知:直线 , 经过直线上的定点的直线交于点 , 点 , 为直线上的两点,且点在点右侧,点的左侧时,连接 , , 满足 . (1)、如图,若 , , 直接写出的度数为: .(2)、如图,射线为的角平分线,用等式表示与之间的数量关系,并证明.18. 如图, , 平分 , 点D,E在射线 , 上,点P是射线上的一个动点,连接交射线于点F,设 .
(1)、如图,若 , , 直接写出的度数为: .(2)、如图,射线为的角平分线,用等式表示与之间的数量关系,并证明.18. 如图, , 平分 , 点D,E在射线 , 上,点P是射线上的一个动点,连接交射线于点F,设 . (1)、如图1,若 .
(1)、如图1,若 .①的度数是 ▲ , 当时,x= ▲ ;
②若 , 求x的值;
(2)、如图2,若 , 是否存在这样的x的值,使得?若存在,求出x的值;若不存在,说明理由.19. (1)、感知与探究:如图①,直线 , 过点作 . 请直接写出 , , 之间的数量关系:;(2)、应用与拓展:如图②,直线 . 若 , , , 借助第(1)问中的结论,求的度数;(3)、方法与实践:如图③,直线 . 若 , , 则 度.20. 在综合与实践课上,老师与同学们以“两条平行线和一块含角的直角三角尺”为主题开展数学活动.
(1)、感知与探究:如图①,直线 , 过点作 . 请直接写出 , , 之间的数量关系:;(2)、应用与拓展:如图②,直线 . 若 , , , 借助第(1)问中的结论,求的度数;(3)、方法与实践:如图③,直线 . 若 , , 则 度.20. 在综合与实践课上,老师与同学们以“两条平行线和一块含角的直角三角尺”为主题开展数学活动. (1)、如图(1),若三角尺的角的顶点放在上,若 , 求的度数;(2)、如图(2),小颖把三角尺的两个锐角的顶点分别放在和上,请你探索并说明与间的数量关系;(3)、如图(3),小亮把三角尺的直角顶点放在上,角的顶点落在上.若 , 则与的数量关系是什么?用含的式子表示.
(1)、如图(1),若三角尺的角的顶点放在上,若 , 求的度数;(2)、如图(2),小颖把三角尺的两个锐角的顶点分别放在和上,请你探索并说明与间的数量关系;(3)、如图(3),小亮把三角尺的直角顶点放在上,角的顶点落在上.若 , 则与的数量关系是什么?用含的式子表示.