2023-2024学年北师大版数学八年级上册 7.3 平行线的判定 同步练习（培优卷）
试卷更新日期：2023-11-18 类型：同步测试
一、选择题
-
1. 下列画出的直线a与b不一定平行的是（ ）A、
B、
C、
D、
2. 如图，下列推论正确的是（ ）
A、 ， B、 ， C、 ， D、 ，3. 下列命题中，是真命题的是（ ）A、同位角相等 B、同旁内角相等，两直线平行 C、若 ， 则 D、对顶角相等4. 如图，点E在AB的延长线上，下列条件中能够判断AD∥BC的是（ ）
A、∠1＝∠3 B、∠C＝∠CBE C、∠C+∠ABC＝180° D、∠2＝∠45. 下列命题：（1）无限循环小数是无理数；（2）绝对值等于它本身的数是非负数；（3）垂直于同一直线的两条直线互相平行；（4）有两边和其中一边的对角对应相等的两个三角形全等；（5）面积相等的两个三角形全等，是假命题的有（ ）A、1个 B、2个 C、3个 D、4个6. 如图，下列条件不能判定的是（ ）
A、 B、 C、 D、7. 如图，能判定EC∥AB的条件是（ ）
A、∠B＝∠ACE B、∠A＝∠ECD C、∠B＝∠ACB D、∠A＝∠ACE8. 如图，BD平分∠ABC，若∠1＝∠2，则（ ）
A、AD＝BC B、AB＝CD C、AB∥CD D、AD∥BC9. 如图，不能推出a∥b的条件是（ ）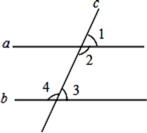
A、∠4＝∠2 B、∠3+∠4＝180° C、∠1＝∠3 D、∠2+∠3＝180°10. 有下列命题：①两点之间，线段最短； ②相等的角是对顶角； ③当a＞0时，|a|＝a； ④内错角互补，两直线平行．其中真命题的有（ ）A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图，AB∥CD，点P到AB，BC，CD的距离相等，则∠P＝
12. 把命题：“内错角相等”改写成“如果......那么......”的形式是.13. 如图，l∥m，等边△ABC的顶点A、B分别在直线l、m上，∠1=25°，则∠2=.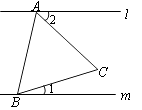
14. 如果两条直线被第三条直线所截，一组同旁内角的度数比为3：2，差为36°，那么这两条直线的位置关系是 ，这是因为 ．15.如图把三角板的直角顶点放在直线b上，若∠1=40°，则当∠2= 度时，a∥b．
三、综合题
-
16. 如图：AE=CF， ∠ A=∠ C， AD=CB，
求证：
(1)、△ADF≌ △CBE；(2)、BE∥DF.17. 如图，AE与BD相交于点C，AC＝EC，BC＝DC，AB＝4cm，点P从点A出发，沿A→B→A方向以3cm/s的速度运动，点Q从点D出发，沿D→E方向以1cm/s的速度运动，P、Q两点同时出发，当点P到达点A时，P、Q两点同时停止运动．设点P的运动时间为t（s）．
(1)、AB与DE有什么关系？请说明理由．(2)、线段AP的长为（用含t的式子表示）．(3)、连接PQ，当线段PQ经过点C时，t的值为 ．18. 如图，点A在MN上，点B在PQ上，连接AB，过点A作 交PQ于点C，过点B作BD平分∠ABC交AC于点D，且 .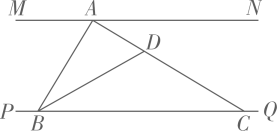
(1)、求证： ；(2)、若 ，求∠ADB的度数.19. 计算与证明．(1)、如图，在中，CD平分 ， 且 ． 求证： ．
(2)、如图，是一个滑梯示意图，若将滑道AC水平放置，则刚好与AB一样长．已知滑梯的高度 ， ， 求滑道AC的长．
20. 如图，∠ACD是等边△ABC的一个外角，点E是∠ACD内部任意一点，作直线CE．
(1)、当CE平分∠ACD时，证明：AB∥CE．(2)、已知点A关于直线CE的对称点为F，连接AF、BF、CF，其中AF、BF分别交直线CE于P、Q两点．记∠ACE＝α，当0＜α＜60°时，求∠BFC，（用含α的式子表示）(3)、若（2）中的α满足0°＜α＜120°时，①∠AFB＝ °；
②探究线段QB、QC、QP之间的数量关系，并证明．