2023-2024学年北师大版数学八年级上册 7.1为什么要证明 同步练习(培优卷)
试卷更新日期:2023-11-18 类型:同步测试
一、单选题
-
1. 我国是最早了解勾股定理的国家之一,它被记载于我国古代的数学著作《周髀算经》中.汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称之为“赵爽弦图”.现在勾股定理的证明已经有400多种方法,下面的两个图形就是验证勾股定理的两种方法,在验证著名的勾股定理过程,这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.在验证过程中它体现的数学思想是 ( )
 A、函数思想 B、数形结合思想 C、分类思想 D、方程思想2. 嘉淇在解决问题时,给出的推理过程如下:
A、函数思想 B、数形结合思想 C、分类思想 D、方程思想2. 嘉淇在解决问题时,给出的推理过程如下:如图,点D在上,点E在上, , ,
求证:.
证明:在和中, ,
∴ , ∴.

小明为保证嘉淇的推理更严谨,想在方框中“∴”和“∴”之间作补充,下列说法正确的是 ( )
A、嘉淇的推理严谨,不需要补充 B、应补充“∴” C、应补充“∴” D、应补充“∴”3. 如图,在中,点D为边上一点,给出如下关系:①平分;②于D;③D为中点.甲说:如果①②同时成立,可证明;乙说:如果②③同时成立,可证明;丙说:如果①③同时成立,可证明.则正确的说法是( ) A、甲、乙正确,丙错误 B、甲正确,乙、丙错误 C、乙正确,甲、丙错误 D、甲、乙、丙都正确4. 法国数学家柯西于1813年在拉格朗日、高斯的基础上彻底证明了《费马多边形数定理》,其主要突破在“五边形数”的证明上,如图为前几个“五边形数”的对应图形,请据此推断,第15个“五边形数”应该为( ),第2021个“五边形数”的奇偶性为( )
A、甲、乙正确,丙错误 B、甲正确,乙、丙错误 C、乙正确,甲、丙错误 D、甲、乙、丙都正确4. 法国数学家柯西于1813年在拉格朗日、高斯的基础上彻底证明了《费马多边形数定理》,其主要突破在“五边形数”的证明上,如图为前几个“五边形数”的对应图形,请据此推断,第15个“五边形数”应该为( ),第2021个“五边形数”的奇偶性为( ) A、330,奇数 B、590,偶数 C、330,偶数 D、590,奇数5. 小明和小亮在研究一道数学题,如图 , , 垂足分别为E、D,G在上.
A、330,奇数 B、590,偶数 C、330,偶数 D、590,奇数5. 小明和小亮在研究一道数学题,如图 , , 垂足分别为E、D,G在上.小明说:“如果 , 则能得到”;
小亮说:“连接 , 如果 , 则能得到”.
则下列判断正确的是( )
 A、小明说法正确,小亮说法错误 B、小明说法正确,小亮说法正确 C、小明说法错误,小亮说法正确 D、小明说法错误,小亮说法错误6. 在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A、过C作EF AB
A、小明说法正确,小亮说法错误 B、小明说法正确,小亮说法正确 C、小明说法错误,小亮说法正确 D、小明说法错误,小亮说法错误6. 在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A、过C作EF AB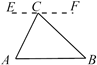 B、过AB上一点D作DE BC,DF AC
B、过AB上一点D作DE BC,DF AC 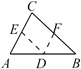 C、延长AC到F,过C作CE AB
C、延长AC到F,过C作CE AB  D、作CD⊥AB于点D
D、作CD⊥AB于点D 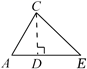 7. 历史上对勾股定理的一种证法采用了下列图形:其中两个全等的直角三角形边AE,EB在一条直线上.证明中用到的面积相等的关系是( )
7. 历史上对勾股定理的一种证法采用了下列图形:其中两个全等的直角三角形边AE,EB在一条直线上.证明中用到的面积相等的关系是( ) A、S△EDA=S△CEB B、S△EDA+S△CEB=S△CDE C、S四边形CDAE=S四边形CDEB D、S△EDA+S△CDE +S△CEB=S四边形ABCD
A、S△EDA=S△CEB B、S△EDA+S△CEB=S△CDE C、S四边形CDAE=S四边形CDEB D、S△EDA+S△CDE +S△CEB=S四边形ABCD二、填空题
-
8. 1930年,德国汉堡大学的学生考拉兹,曾经提出过这样一个数学猜想:对于每一个正整数,如果它是奇数,则对它乘再加;如果它是偶数,则对它除以如此循环,最终都能够得到这一猜想后来成为著名的“考拉兹猜想”,又称“奇偶归一猜想”虽然这个结论在数学上还没有得到证明,但举例验证都是正确的,例如:正整数经过下面步运算可得到 , 即:则正整数经过步运算可得到 . 那么正整数经过步运算可得到 .
三、综合题
-
9. 如图 , 在一张白纸上画直线 , 点在直线外;如图所示,翻折白纸使直线重合,折痕经过点 , 记折痕为直线;再次如图所示,翻折白纸,使图中的直线重合,经过点的新的折痕记为直线;如图 , 请根据以上操作说明直线 , 的位置关系,并证明你的结论.
 10. 实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等,如图1,一束光线射到平面镜上,被反射后的光线为 , 则入射光线 , 反射光线与平面镜所夹的锐角 .
10. 实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等,如图1,一束光线射到平面镜上,被反射后的光线为 , 则入射光线 , 反射光线与平面镜所夹的锐角 .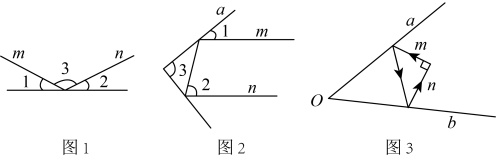 (1)、如图2,一束光线射到平面镜上,被反射到平面镜上,又被反射,若被反射出的光线与光线平行,且 , 则 , ;(2)、图2中,当被反射出的光线与光线平行时,不论如何变化,与总具有一定的数量关系,请你探究和的数量关系,并说明理由;(3)、图2中,由(1)、(2),请你探究:当任何射到平面镜上的光线 , 经过平面镜、的两次反射后,入射光线与反射光线平行,求两平面镜、的夹角的度数,并说明理由.(4)、如图3,一束光线射到平面镜上,被反射到平面镜上,又被反射,若被反射出的光线与光线垂直,则等于多少度?(友情提示:三角形内角和等于 )11. 实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)、如图2,一束光线射到平面镜上,被反射到平面镜上,又被反射,若被反射出的光线与光线平行,且 , 则 , ;(2)、图2中,当被反射出的光线与光线平行时,不论如何变化,与总具有一定的数量关系,请你探究和的数量关系,并说明理由;(3)、图2中,由(1)、(2),请你探究:当任何射到平面镜上的光线 , 经过平面镜、的两次反射后,入射光线与反射光线平行,求两平面镜、的夹角的度数,并说明理由.(4)、如图3,一束光线射到平面镜上,被反射到平面镜上,又被反射,若被反射出的光线与光线垂直,则等于多少度?(友情提示:三角形内角和等于 )11. 实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等. (1)、如图,一束光线m射到平面镜上,被反射到平面镜b上,又被b反射,若被b反射出的光线n与光线m平行,且 , 则 , .(2)、在(1)中,若 , 则;若 , 则;(3)、由(1)、(2),请你猜想:当两平面镜、的夹角 时,可以使任何射到平面镜上的光线m,经过平面镜、的两次反射后,入射光线m与反射光线n平行.请说明理由.12. 数学探究活动中,阿青同学为了验证:长条纸片上下边沿与是否平行,把纸片沿着折叠(如图1),并用量角器测出的度数;
(1)、如图,一束光线m射到平面镜上,被反射到平面镜b上,又被b反射,若被b反射出的光线n与光线m平行,且 , 则 , .(2)、在(1)中,若 , 则;若 , 则;(3)、由(1)、(2),请你猜想:当两平面镜、的夹角 时,可以使任何射到平面镜上的光线m,经过平面镜、的两次反射后,入射光线m与反射光线n平行.请说明理由.12. 数学探究活动中,阿青同学为了验证:长条纸片上下边沿与是否平行,把纸片沿着折叠(如图1),并用量角器测出的度数;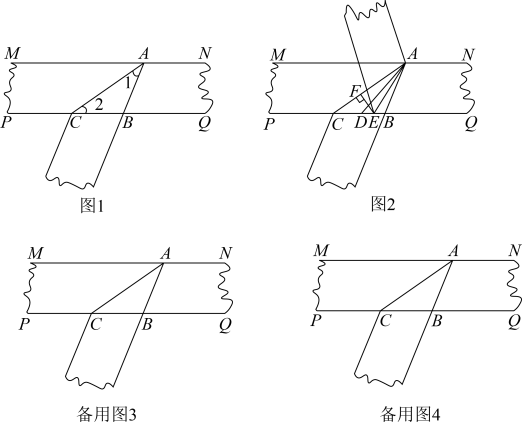 (1)、若 , 则.你认为阿青同学的做法正确吗?㳻说明理由;(2)、在(1)的条件下,阿青同学在纸条下上取点(如图2),连结并沿着折叠纸片使得与重合,过作于点 , 设 , .
(1)、若 , 则.你认为阿青同学的做法正确吗?㳻说明理由;(2)、在(1)的条件下,阿青同学在纸条下上取点(如图2),连结并沿着折叠纸片使得与重合,过作于点 , 设 , .①当点在点之间时,若 , 求的度数;
②当点在上的运动过程中,和之间有怎样的数量关系?请写出你的猜想,并加以证明.(选其中一种情况证明)
13. 在单位长度为1的正方形网格中,如果一个凸多边形的顶点都是网格线交点,我们称其为格点凸多边形,并记该格点多边形的面积为S,多边形内部的格点数为N,多边形边上的格点数为L.(1)、对于图中的五个凸多边形,补全以下表格: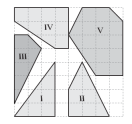
多边形
面积S
内部格点数N
边上格点数L
Ⅰ
Ⅱ
7
4
8
8
Ⅲ
Ⅳ
9
5
10
10
Ⅴ
11
11
(2)、借助以上表格猜想格点凸多边形的面积公式:S与的数量关系可用等式表示为;(3)、已知格点长方形ABCD,设其边长 , 其中m,n为正整数.请以格点长方形为例,尝试证明(2)中的格点凸多边形的面积公式.14.(1)、计算并观察下列各式:第1个:;
第2个:;
第3个:;
……
这些等式反映出多项式乘法的某种运算规律.
(2)、猜想:若n为大于1的正整数,则;(3)、利用(2)的猜想计算: .(4)、拓广与应用: .15. 根据学习“数与式”的经验,通过由“特殊到一般”的方法探究下面二次根式的运算规律.以下是探究过程,请补充完整.(1)、具体运算,发现规律.特例1. . 特例2. , 特例3. , 特例4. ,
特例5. .
(2)、观察、归纳,得出猜想.如果n为正整数,用含n的式子表示上述的运算规律为: .
(3)、证明你的猜想.16. 观察下列图形与等式的关系:
按照以上图形与等式的规律,解答下列问题:
(1)、写出第5个等式: .(2)、写出你猜想的第n个等式: ▲ . (用含n的等式表示),并证明(已知:1+2+3+……+n=).17. 【阅读】在证明命题“如果 , , 那么”时,小明的证明方法如下:证明:∵ ,
∴> ▲ . ∴ ▲ .
∵ , ,
∴ ▲ . ∴ ▲ .
∴.
【问题解决】
(1)、请将上面的证明过程填写完整;(2)、有以下几个条件:① , ② , ③ , ④ .请从中选择两个作为已知条件 , 得出结论 .你选择的条件序号是 ,并给出证明过程 .18. 定义:如果一个正整数n能表示为两个正整数的平方差,那么称正整数n为“智慧数”,即:若正整数n=a2-b2(a,b为正整数,且a>b),则称正整数n为“智慧数”.例如:∵5=32-22 , ∴5是“智慧数”.根据定义,直接写出最小的“智慧数”是 .
提出问题:
如果按照从小到大的顺序排列起来,那么第2022个“智慧数”是哪位数?
探究问题:
要解答这个问题,我们先要明白“智慧数”产生的规律.
探究1:“智慧数”一定是什么数?
假设n是“智慧数”,则至少存在一组正整数a、b,使n=a2-b2(a,b为正整数,且a>b).
情况1:a、b均为奇数,或均为偶数.
分析:
∵a、b均为奇数,或均为偶数
∴(a+b)、(a-b)均为偶数
此时不妨设(a+b)=2c,(a-b)=2d
又∵n=a2-b2=(a+b)(a-b)=4cd
∴a2-b2为4的倍数,即n为4的倍数.
情况2:a、b为一奇数、一偶数.
分析:
∵a、b为一奇数、一偶数
∴(a+b)、(a-b)均为奇数
此时不妨设(a+b)=2c1,(a-b)=2d1
又∵n=a2-b2=(a+b)(a-b)=4cd2c2d1
∴a2-b2为奇数,即n为奇数.
综上所述:“智慧数”为奇数或4的倍数.
探究2:所有奇数和4的倍数都一定“智慧数”吗?
我们先从最简单的情形入手,从中找到解决问题的方法,最后得出一般性的结论.
先举例几组数值较小,容易验证的“智慧数”(①--⑧),因为“智慧数”不是奇数就是4的倍数,所以我们把这“智慧数”分成两类.
情况1:n是奇数
分析n=a2-b2
结论
①
3是“智慧数”
②
5是“智慧数”
③
7是“智慧数”
④
9是“智慧数”
……
……
……
情况2:n是4的倍数
分析n=a2-b2
结论
⑤
8是“智慧数”
⑥
12是“智慧数”
⑦
16是“智慧数”
⑧
20是“智慧数”
……
……
……
情况1:n是奇数
观察①②③④中n、a、b的值,容易发现,每个算式中,n均是奇数,且a、b的值均为连续的正整数.
猜想:所有奇数都是“智慧数”.
验证:设a=k+1,b=k(k≥1,且k为整数)
∵a2-b2=(k+1)2-k2=2k+1
∴2k+1是“智慧数”
又∵k≥1
∴2k+1≥3,即2k+1表示所有奇数(1除外)
∴所有奇数(1除外)都是“智慧数”
应用:
请直接填空:∵11= 2-2 ∴11是“智慧数”
情况2:n是4的倍数.
观察⑤⑥⑦⑧中n、a、b的值,容易发现,每个算式中,n均是4的倍数,且a、b的差都为2.
猜想:所有4的倍数都是“智慧数”.
验证:设a=k+2,b=k(k≥1,且k为整数)
∵a2-b2=(k+2)2-k2=4k+4
∴4k+4是“智慧数”
又∵k≥1
∴4k+4≥8,即4k+4表示所有4的倍数(4除外)
∴所有4的倍数(4除外)都是“智慧数”
应用:
请直接填空:∵24= 2- 2 ∴24“智慧数”
归纳“智慧数”的发现模型:
⑴对所有的正整数而言,除了1和4之外,其余的奇数以及4的倍数是智慧数.
⑵当1≤n≤4时,只有1个“智慧数”;
当n≥5时,如果把从5开始的正整数按照从小到大的顺序,依次每个连续正整数分成一组(注:组与组之间的数字互不重复),则每组有个“智慧数”,且第个数不是“智慧数”.
问题解决:
直接写出:如果按照从小到大的顺序排列起来,那么第2022个“智慧数”是 .
实际应用:
若一个直角三角形纸片三边的长度都是整数厘米,已知一条直角边长是12cm,则这个直角三角形纸片的周长最大是cm.
19. 勾股定理神秘而美妙,它的验证方法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜地发现,当两个全等的直角三角形如图①或图②所示摆放时,都可以用“面积法”来验证,下面是小聪利用图①验证勾股定理的过程: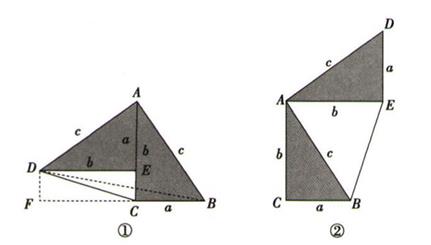
将两个全等的直角三角形按如图①所示摆放,其中∠DAB=90°,试说明:a2+b2=c2
解:连接DB,过点D作BC边上的高DF,则DF=EC=b-a
因为S四边形ADCB= S△ADB+S△ABC= b2+ ab,
S四边形BADCB=S△ADB+S△DCB= c2+ a(b-a),
所以 b2+ ab= c2+ a(b-a),
所以a2+b2=c2
请参照上述验证方法,利用图②说明a2+b°2=c2
20. 阅读与理解:折纸,常常能为证明一个命题提供思路和方法,例如,在△ABC中,AB>AC(如图),怎样证明∠C>∠B呢?
分析:把AC沿∠A的角平分线AD翻折,因为AB>AC,所以点C落在AB上的点C’处,即AC=AC’,据以上操作,易证明△ACD AC’D,所以∠AC’D=∠C,又因为∠AC’D>∠B,所以∠C>∠B.
感悟与应用:
 (1)、如图(1)在△ABC中,∠ACB=90°,∠B=30°,CD平分∠ACB,试判断AC和AD、BC之间的数量关系,并说明理由;(2)、如图(3),在四边形ABCD中,AC平分∠DAB,AC=4,AD=2,CD=BC=3,
(1)、如图(1)在△ABC中,∠ACB=90°,∠B=30°,CD平分∠ACB,试判断AC和AD、BC之间的数量关系,并说明理由;(2)、如图(3),在四边形ABCD中,AC平分∠DAB,AC=4,AD=2,CD=BC=3,①求证:∠B+∠D=180°;
②求AB的长.
-