2023年九年级上册数学人教版单元分层测试 第二十四章 圆 B卷
试卷更新日期:2023-11-17 类型:单元试卷
一、选择题
-
1. ⊙O的半径为2,则它的内接正六边形的边长为( )A、2 B、2 C、 D、22. 如图,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时位于弧AB上,此时∠AOE=56°,则α的度数是( ).
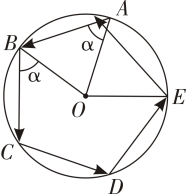 A、52° B、60° C、72° D、76°3. 在Rt△ABC中,∠C=90°,AC=3,BC=4,则它的外心与直角顶点的距离是( ).A、2 B、2.5 C、3 D、44. 数学课上,老师让学生用尺规作图作Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的作法如图所示,你认为这种作法能判断∠ACB是直角的依据是( ).
A、52° B、60° C、72° D、76°3. 在Rt△ABC中,∠C=90°,AC=3,BC=4,则它的外心与直角顶点的距离是( ).A、2 B、2.5 C、3 D、44. 数学课上,老师让学生用尺规作图作Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的作法如图所示,你认为这种作法能判断∠ACB是直角的依据是( ). A、勾股定理 B、直径所对的圆周角是直角 C、勾股定理的逆定理 D、90°的圆周角所对的弦是直径5. 如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点).以A为圆心,r为半径作图.选取的格点中,若除A外恰好有3个在圆内,则r的取值范围为( ).
A、勾股定理 B、直径所对的圆周角是直角 C、勾股定理的逆定理 D、90°的圆周角所对的弦是直径5. 如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点).以A为圆心,r为半径作图.选取的格点中,若除A外恰好有3个在圆内,则r的取值范围为( ). A、<r< B、<r< C、<r<5 D、5<r<6. 如图,AB是⊙O的弦,OC⊥AB,交⊙O于点C,连结OA,OB,BC.若∠ABC= 20°,则∠AOB的度数是( ).
A、<r< B、<r< C、<r<5 D、5<r<6. 如图,AB是⊙O的弦,OC⊥AB,交⊙O于点C,连结OA,OB,BC.若∠ABC= 20°,则∠AOB的度数是( ). A、40° B、50° C、70° D、80°7. 如图,BC是⊙O的直径,A是⊙O上的一点.若∠OAC=32°,则∠B的度数是( ).
A、40° B、50° C、70° D、80°7. 如图,BC是⊙O的直径,A是⊙O上的一点.若∠OAC=32°,则∠B的度数是( ). A、58° B、60° C、64° D、68°8. 已知点A,B,C在⊙O上,∠ABC=30°,把劣弧沿着直线CB折叠交弦AB于点D.若BD=9,AD=6,则的长为( )
A、58° B、60° C、64° D、68°8. 已知点A,B,C在⊙O上,∠ABC=30°,把劣弧沿着直线CB折叠交弦AB于点D.若BD=9,AD=6,则的长为( ) A、π B、3π C、π D、π9. 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( ).
A、π B、3π C、π D、π9. 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( ).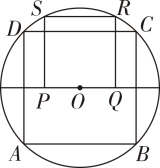 A、1 :2 B、1:3 C、2:3 D、2:510. 如图,AB=4,以O为圆心,AB为直径作半圆,点C是半圆一动点,若BC=2BD,∠CBD=60°,则线段AD的最大值为( )
A、1 :2 B、1:3 C、2:3 D、2:510. 如图,AB=4,以O为圆心,AB为直径作半圆,点C是半圆一动点,若BC=2BD,∠CBD=60°,则线段AD的最大值为( )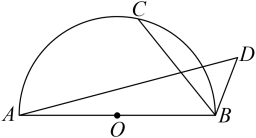 A、2+2 B、+1 C、3 D、2+1
A、2+2 B、+1 C、3 D、2+1二、填空题
-
11. 如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM的度数是
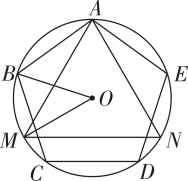 12. 如图,四边形ABDC是⊙O的内接四边形,∠BOC=110°,则∠BDC的大小为
12. 如图,四边形ABDC是⊙O的内接四边形,∠BOC=110°,则∠BDC的大小为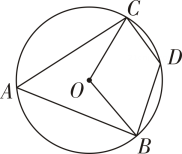 13. 如图,EF是⊙O的直径,把∠A为45°的直角三角尺ABC的一条直角边BC放在直线EF上,斜边AB所在直线与⊙O交于点P,点B,O重合,且AC大于OE.将三角尺ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x°,则x的取值范围是
13. 如图,EF是⊙O的直径,把∠A为45°的直角三角尺ABC的一条直角边BC放在直线EF上,斜边AB所在直线与⊙O交于点P,点B,O重合,且AC大于OE.将三角尺ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x°,则x的取值范围是 14. 已知正六边形的边长为4cm,分别以它的三个不相邻的顶点为圆心,边长为半径作弧(如图),则所得到的三条弧的长度之和为cm.(结果保留π)
14. 已知正六边形的边长为4cm,分别以它的三个不相邻的顶点为圆心,边长为半径作弧(如图),则所得到的三条弧的长度之和为cm.(结果保留π) 15. 如图所示,在中,是线段BC上的一个动点,以AD为直径画分别交AB,AC于E,F,连结EF,则EF的最小值为.
15. 如图所示,在中,是线段BC上的一个动点,以AD为直径画分别交AB,AC于E,F,连结EF,则EF的最小值为. 16. 如图,点P是线段AB上一动点(不包括端点),过点P作PQ⊥AB交以AB为直径的半圆O于点Q,连结AQ,过点P作PC∥AQ交该半圆于点C,连结CB.当△PCB是以PC为腰的等腰三角形时,为
16. 如图,点P是线段AB上一动点(不包括端点),过点P作PQ⊥AB交以AB为直径的半圆O于点Q,连结AQ,过点P作PC∥AQ交该半圆于点C,连结CB.当△PCB是以PC为腰的等腰三角形时,为
三、解答题
-
17. 如图,在正六边形ABCDEF中,AB=2,P是ED的中点,连结AP.求AP的长.
 18. 如图,在半径为5的扇形OAB中,∠AOB=90°,C是上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为点D,E.
18. 如图,在半径为5的扇形OAB中,∠AOB=90°,C是上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为点D,E. (1)、当BC=6时,求线段OD的长.(2)、求DE的长.(3)、在△ODE中,是否存在度数不变的角?若存在,请直接指出是哪个角,并求出它的度数.19. 如图,已知为的直径,是弦,且于点 , 连接、、 .
(1)、当BC=6时,求线段OD的长.(2)、求DE的长.(3)、在△ODE中,是否存在度数不变的角?若存在,请直接指出是哪个角,并求出它的度数.19. 如图,已知为的直径,是弦,且于点 , 连接、、 . (1)、求证:;(2)、若 , , 求的半径.
(1)、求证:;(2)、若 , , 求的半径.四、综合题

