2023年九年级上册数学人教版单元分层测试 第二十四章 圆 A卷
试卷更新日期:2023-11-17 类型:单元试卷
一、选择题
-
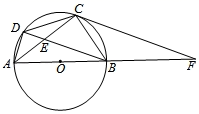
1. 已知圆O的半径为5,同一平面内有一点P,且OP=4,则点P与圆O的关系是( )A、点P在圆内 B、点P在圆外 C、点P在圆上 D、无法确定2. 下列命题为真命题的是( ).A、三点确定一个圆 B、度数相等的弧相等 C、90°的圆周角所对的弦是直径 D、相等的圆心角所对的弧相等,所对的弦也相等3. 已知扇形的面积为30πcm2 , 它的半径为4cm,则扇形的弧长为( ).A、10π cm B、15πcm C、20πcm D、25πcm4. 如图,AB是⊙O的直径,弦CD⊥AB于点E.若OC=5 cm,CD=6 cm,则AE=( ).
 A、4cm B、3cm C、9cm D、8cm5. 如图,点A,B,C是⊙O上的点,且∠ACB=40°,阴影部分的面积为2π,则此扇形的半径为( ).
A、4cm B、3cm C、9cm D、8cm5. 如图,点A,B,C是⊙O上的点,且∠ACB=40°,阴影部分的面积为2π,则此扇形的半径为( ). A、2 B、3 C、4 D、56. 如图,四边形ABCD内接于⊙O,四边形ABCO是平行四边形,则∠ADC的度数是( ).
A、2 B、3 C、4 D、56. 如图,四边形ABCD内接于⊙O,四边形ABCO是平行四边形,则∠ADC的度数是( ). A、45° B、50° C、60° D、75°7. 年北京冬奥会开幕式为世界奉献了一场精彩、简约、唯美、浪漫的中国文化盛宴,其中主火炬台的雪花状创意令人惊叹.如图是一个正六边形雪花状饰品,则它的每一个内角是( )
A、45° B、50° C、60° D、75°7. 年北京冬奥会开幕式为世界奉献了一场精彩、简约、唯美、浪漫的中国文化盛宴,其中主火炬台的雪花状创意令人惊叹.如图是一个正六边形雪花状饰品,则它的每一个内角是( ) A、 B、 C、 D、8. 一块等边三角形木板,边长为1,现将木板沿水平线翻滚(如图),那么点B从开始至结束所经过的路径长为( ).
A、 B、 C、 D、8. 一块等边三角形木板,边长为1,现将木板沿水平线翻滚(如图),那么点B从开始至结束所经过的路径长为( ).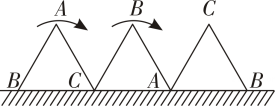 A、 B、 C、4 D、2+9. 如图,BC是半圆O的直径,D,E是上两点,连结BD,CE并延长,交于点A,连结OD,OE.若∠A=70° ,则∠DOE的度数为( ).
A、 B、 C、4 D、2+9. 如图,BC是半圆O的直径,D,E是上两点,连结BD,CE并延长,交于点A,连结OD,OE.若∠A=70° ,则∠DOE的度数为( ). A、35° B、38° C、40° D、42°10. 如图,以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点,交直角边AC于点E,且B,E是半圆弧的三等分点.若的长为 , 则图中阴影部分的面积为( ).
A、35° B、38° C、40° D、42°10. 如图,以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点,交直角边AC于点E,且B,E是半圆弧的三等分点.若的长为 , 则图中阴影部分的面积为( ). A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 与圆有关的角有哪些?。同弧所对的圆周角等于圆心角的。12. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上,点A,B的读数分别为86°,30°,则∠ACB的大小为
 13. 如图,边长为2的等边△ABC,将边BC不改变长度,变为 , 得到以A为圆心,AB为半径的扇形ABC,则此扇形的面积为
13. 如图,边长为2的等边△ABC,将边BC不改变长度,变为 , 得到以A为圆心,AB为半径的扇形ABC,则此扇形的面积为 14. 如图,是的内接三角形,是的直径, , 的平分线交于点 , 则的度数是 .
14. 如图,是的内接三角形,是的直径, , 的平分线交于点 , 则的度数是 .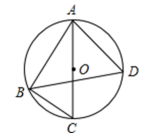 15. 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均落在格点上.用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面的半径是
15. 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均落在格点上.用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面的半径是 16. 如图,⊙O是△ABC的外接圆,BC是⊙O的直径,AB=AC.∠ABC的平分线交AC于点D,交⊙O于点E,连结CE.若CE= , 则BD的长为
16. 如图,⊙O是△ABC的外接圆,BC是⊙O的直径,AB=AC.∠ABC的平分线交AC于点D,交⊙O于点E,连结CE.若CE= , 则BD的长为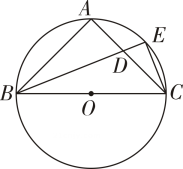
三、作图题
-
17. 如图,已知⊙O,用直尺和圆规作⊙O的内接正三角形.
 18. 如图,在平面直角坐标系中,的三个顶点坐标分别为 , , .
18. 如图,在平面直角坐标系中,的三个顶点坐标分别为 , , .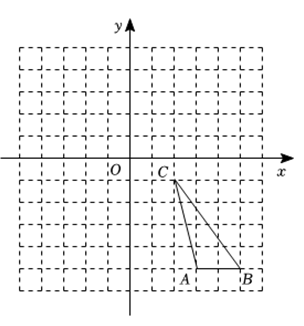
⑴画出关于轴对称的;
⑵画出绕点顺时针旋转后的;⑶在的条件下,求线段扫过的面积结果保留 .
四、解答题
-
19. 如图,△ABC是⊙O的内接三角形,AD是⊙O的直径.若∠ABC=50°,求∠CAD的度数.
 20. 如图,⊙O的直径AB和弦CD相交于点E.已知AE=1,EB=5,∠DEB=60°,求CD 的长.
20. 如图,⊙O的直径AB和弦CD相交于点E.已知AE=1,EB=5,∠DEB=60°,求CD 的长. 21. 已知:如图,OA=OB,AB交⊙O于点C,D.
21. 已知:如图,OA=OB,AB交⊙O于点C,D.求证:AC=BD.
 22. 如图,半圆ACB中,点D是的中点,点E在直径AB上,且AE=AC,半径OD交CE于点F.
22. 如图,半圆ACB中,点D是的中点,点E在直径AB上,且AE=AC,半径OD交CE于点F. (1)、求证:OF=OE:(2)、若OF=6,DF=4,求CF的长.
(1)、求证:OF=OE:(2)、若OF=6,DF=4,求CF的长.五、综合题