2023年九年级上册数学人教版单元分层测试 第二十三章 旋转 B卷
试卷更新日期:2023-11-17 类型:单元试卷
一、选择题
-
1. 下列图案中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 将如图所示的图案绕其中心旋转n°时与原图案重合,则n的最小值是( ).
2. 将如图所示的图案绕其中心旋转n°时与原图案重合,则n的最小值是( ).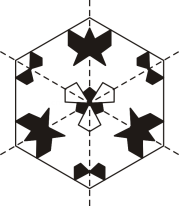 A、60 B、90 C、120 D、1803. 如图所示,Rt的斜边在轴上, , 含角的顶点与原点重合,直角顶点在第二象限,将Rt绕原点按顺时针方向旋转后得到 , 则点的对应点的坐标为( ).
A、60 B、90 C、120 D、1803. 如图所示,Rt的斜边在轴上, , 含角的顶点与原点重合,直角顶点在第二象限,将Rt绕原点按顺时针方向旋转后得到 , 则点的对应点的坐标为( ). A、 B、 C、 D、4. 下列说法中,正确的有( ).
A、 B、 C、 D、4. 下列说法中,正确的有( ).①图形旋转时,图形上的每一个点都绕旋转中心旋转了相同的角度;
②图形旋转时,对应点与旋转中心的距离相等;
③图形旋转时,对应线段相等,对应角相等,图形的形状和大小不变;
④两个图形成中心对称,可看作是一个图形绕着对称中心旋转180°得到另一个图形.A、1个 B、2个 C、3个 D、4个5. 如图所示,已知在6×4的正方形网格中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( ). A、点 B、点 C、点 D、点6. 如图所示,把是直角的绕点按顺时针方向旋转 , 把点转到点得 , 则下列结论中,错误的是( ).
A、点 B、点 C、点 D、点6. 如图所示,把是直角的绕点按顺时针方向旋转 , 把点转到点得 , 则下列结论中,错误的是( ). A、 B、 C、 D、7. 在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1 , 则其旋转中心可能是( )
A、 B、 C、 D、7. 在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1 , 则其旋转中心可能是( ) A、点A B、点B C、点C D、点D8. 如图所示,矩形ABOC的顶点O(0,0),A(-2 , 2),对角线交点为P,若矩形绕点O逆时针旋转,每次旋转90°,则第74次旋转后点P的落点坐标为( )
A、点A B、点B C、点C D、点D8. 如图所示,矩形ABOC的顶点O(0,0),A(-2 , 2),对角线交点为P,若矩形绕点O逆时针旋转,每次旋转90°,则第74次旋转后点P的落点坐标为( ) A、(1,) B、(2,0) C、(1,-) D、( , -1)9. 如图,在△ABC中,AB=AC=4,∠BAC=120°,P为BC边上一动点,连接AP,将线段AP绕点A顺时针旋转120°至AP′,则线段PP′的最小值为( )
A、(1,) B、(2,0) C、(1,-) D、( , -1)9. 如图,在△ABC中,AB=AC=4,∠BAC=120°,P为BC边上一动点,连接AP,将线段AP绕点A顺时针旋转120°至AP′,则线段PP′的最小值为( )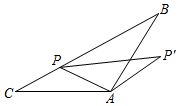 A、 B、 C、 D、10. 已知,矩形中, , , 点是线段上的一个动点,将线段绕点逆时针旋转得到 , 过作于点 , 连接 , 取的中点 , 连接 , . 点在运动过程中,下列结论:
A、 B、 C、 D、10. 已知,矩形中, , , 点是线段上的一个动点,将线段绕点逆时针旋转得到 , 过作于点 , 连接 , 取的中点 , 连接 , . 点在运动过程中,下列结论:
①;②当点和点互相重合时,;③;④ . 正确的有( )个.
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,将绕点顺时针旋转得到 , 点的对应点恰好落在边上,则 .
 12. 如图,已知正方形的边长为 , 为边上一点,以点为中心,把顺时针旋转 , 得 , 连接 , 则的长等于 .
12. 如图,已知正方形的边长为 , 为边上一点,以点为中心,把顺时针旋转 , 得 , 连接 , 则的长等于 .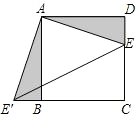 13. 如图,将绕点顺时针旋转角 , 得到 , 若 , , 则的度数为 .
13. 如图,将绕点顺时针旋转角 , 得到 , 若 , , 则的度数为 .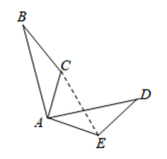 14. 如图1,一款暗插销由外壳AB , 开关CD , 其工作原理如图2,开关CD绕固定点O转动,此时连接点D在线段AB上,如D1位置.开关CD绕点O顺时针旋转180°后得到C2D2 , 锁芯弹回至D2E2位置(点B与点E2重合),此时插销闭合如图4.已知CD=74mm , AD2-AC1=50mm , 则BE1=mm .
14. 如图1,一款暗插销由外壳AB , 开关CD , 其工作原理如图2,开关CD绕固定点O转动,此时连接点D在线段AB上,如D1位置.开关CD绕点O顺时针旋转180°后得到C2D2 , 锁芯弹回至D2E2位置(点B与点E2重合),此时插销闭合如图4.已知CD=74mm , AD2-AC1=50mm , 则BE1=mm . 15. 如图,将边长为的正方形绕点按逆时针方向旋转,得到正方形 , 连接 , , 在旋转角从到的整个旋转过程中,当时,的面积为 .
15. 如图,将边长为的正方形绕点按逆时针方向旋转,得到正方形 , 连接 , , 在旋转角从到的整个旋转过程中,当时,的面积为 .
三、作图题
-
16. 如图,网格中每个小正方形的边长均为1,点、在小正方形的顶点上.
 (1)、画出以为腰的等腰直角(点在小正方形的顶点上)(2)、画出以为一边且面积为的平行四边形 , (点、都在小正方形的顶点上).17. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)、画出以为腰的等腰直角(点在小正方形的顶点上)(2)、画出以为一边且面积为的平行四边形 , (点、都在小正方形的顶点上).17. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4). (1)、请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(1)、请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)、请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)、在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
四、解答题
-
18. 如图,四边形是正方形,点为内一点,将绕点顺时针旋转得到 , 连接、、 , 与交于点 .
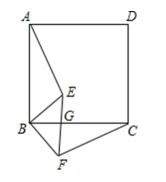 (1)、求证:;(2)、若 , 求的大小.19. 如图,在五边形ABCDE中, , 连接AC , AD , .
(1)、求证:;(2)、若 , 求的大小.19. 如图,在五边形ABCDE中, , 连接AC , AD , . (1)、已知 , 则 .(2)、求五边形ABCDE的周长.
(1)、已知 , 则 .(2)、求五边形ABCDE的周长.【注:五边形的周长指组成五边形的所有边的和】
20. 在Rt△ABC中,∠ABC=90°,∠BAC=α,D为AB的中点,过D作DE⊥AC于E,连接CD,F为CD的中点. (1)、图1中,BF与EF的数量关系是 , ∠BFE=(用含α的式子表示);(2)、将△ADE绕点A逆时针旋转至如图2所示位置,试判断(1)中的两个结论是否依然成立?若成立,请证明你的结论.
(1)、图1中,BF与EF的数量关系是 , ∠BFE=(用含α的式子表示);(2)、将△ADE绕点A逆时针旋转至如图2所示位置,试判断(1)中的两个结论是否依然成立?若成立,请证明你的结论.五、综合题
-
21. 如图,在平面直角坐标系中,直线与x轴、y轴相交于A、B两点,动点C在线段上,将线段绕着点C顺时针旋转得到 , 此时点D恰好落在直线上时,过点D作轴于点E .
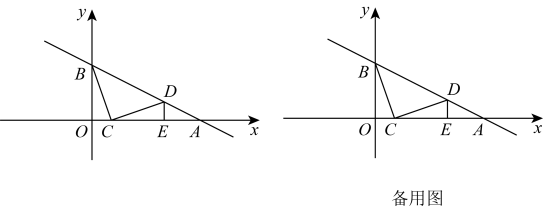 (1)、求证:;(2)、求点D的坐标;(3)、若点P在y轴上,点Q在直线上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标;若不存在,请说明理由.22. 在△ABC中,∠ACB=90°,∠ABC=30°,AC=2cm,△ABC绕点C顺时针旋转,旋转角为α(0°<α<180°),点A、B的对应点分别是D , E .
(1)、求证:;(2)、求点D的坐标;(3)、若点P在y轴上,点Q在直线上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标;若不存在,请说明理由.22. 在△ABC中,∠ACB=90°,∠ABC=30°,AC=2cm,△ABC绕点C顺时针旋转,旋转角为α(0°<α<180°),点A、B的对应点分别是D , E . (1)、如图1,当点D恰好落在边AB上时,旋转角α的度数是 ▲ ;(2)、如图2,当点B , D , E三点恰好在同一直线上时,判断此时直线CE与AB的位置关系,并说明理由;(3)、如图3,当B , D , E三点不在同一直线上时,连接BD , AE , 若△BCD的面积为cm2 , 求此时四边形ABDE的面积.
(1)、如图1,当点D恰好落在边AB上时,旋转角α的度数是 ▲ ;(2)、如图2,当点B , D , E三点恰好在同一直线上时,判断此时直线CE与AB的位置关系,并说明理由;(3)、如图3,当B , D , E三点不在同一直线上时,连接BD , AE , 若△BCD的面积为cm2 , 求此时四边形ABDE的面积.