浙江省杭州绍兴宁波七地八校九年级联考2023-2024学年九年级上册数学期中考试试卷
试卷更新日期:2023-11-17 类型:期中考试
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 的半径为 ,若点 到圆心的距离为 ,点 在( )A、圆内 B、圆上 C、圆外 D、无法确定2. 下列事件中,不可能事件( )A、任意选择某一电视频道,它正播放动画片 B、任意掷一枚硬币,正面朝上 C、在只装有红球的袋子里摸出一个黑球 D、射击运动员射击一次,命中10环3. 已知 , 则的值为( )A、 B、 C、 D、4. 将二次函数y=2x2的图象先向上平移3个单位,再向右平移4个单位所得图象的解析式为( )A、y=2(x-4)2+3 B、y=2(x+4)2-3 C、y=2(x+4)2+3 D、y=2(x-4)2-35. 如图,点A、B、C在⊙O上,∠ACB=40°,弧AB的度数为( )
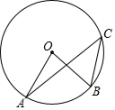 A、80° B、40° C、20° D、60°6. 如图,直线l1∥l2∥l3 , 直线AB,DE分别交l1 , l2 , l3于点A,B,C和D,E,F,若AB:AC=2:5,EF=15,则DF的长等于( )
A、80° B、40° C、20° D、60°6. 如图,直线l1∥l2∥l3 , 直线AB,DE分别交l1 , l2 , l3于点A,B,C和D,E,F,若AB:AC=2:5,EF=15,则DF的长等于( )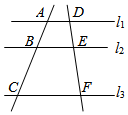 A、18 B、20 C、25 D、307. 下列命题正确的是( )A、三个点确定一个圆 B、平分弦的直径垂直于弦,并且平分弦所对的弧 C、圆内接平行四边形一定是矩形 D、在同圆或等圆中,弦相等则所对的弧相等8. 我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知大小,用锯子去锯这个木材,锯口深DE=1寸,锯道AB=1尺(1尺=10寸),则这根圆柱形木材的直径是( )
A、18 B、20 C、25 D、307. 下列命题正确的是( )A、三个点确定一个圆 B、平分弦的直径垂直于弦,并且平分弦所对的弧 C、圆内接平行四边形一定是矩形 D、在同圆或等圆中,弦相等则所对的弧相等8. 我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知大小,用锯子去锯这个木材,锯口深DE=1寸,锯道AB=1尺(1尺=10寸),则这根圆柱形木材的直径是( )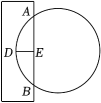 A、12寸 B、13寸 C、24寸 D、26寸9. 如图,在平面直角坐标系xOy中,函数y=ax2+bx+c的图象与对称轴直线x=m交于点A,与x,y轴交于B,C,D三点,下列命题正确的是( )
A、12寸 B、13寸 C、24寸 D、26寸9. 如图,在平面直角坐标系xOy中,函数y=ax2+bx+c的图象与对称轴直线x=m交于点A,与x,y轴交于B,C,D三点,下列命题正确的是( )
①abc>0;②若B的坐标为(-m,0),则C的坐标为(3m,0);
③对于任意x0(x0≠m),始终有ax02+bx0>am2+bm;
④若OD=OC,则ac+b+1=0.
A、①②③ B、①②④ C、①③④ D、②③④10. 如图,点O在线段AB上,OA=2,OB=6,以O为圆心,OA为半径作⊙O,点M在⊙O上运动,连结MB,以MB为一边作等边△MBC,连结AC,则AC长度的最小值为( )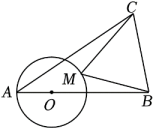 A、22 B、22 C、42 D、42
A、22 B、22 C、42 D、42二、填空题(本题有6小题,每小题4分,共24分)
-
11. 已知,点A(-1,y1),B(-0.5,y2),C(4,y3)都在二次函数y=x2-2x-1的图象上,则y1 , y2 , y3的大小关系是(用“<”连接).12. 某学习小组做抛掷一枚瓶盖的实验,整理的实验数据如表:
累计抛掷次数
50
100
200
300
500
1000
2000
3000
5000
盖面朝上次数
28
54
106
158
264
527
1056
1587
2650
盖面朝上频率
0.5600
0.5400
0.5300
0.5267
0.5280
0.5270
0.5280
0.5290
0.530
随着实验次数的增大,“盖面朝上”的概率接近于(精确到0.01).
13. 将量角器按如图所示的方式放置在三角形纸片上,使点C在半圆圆心上,点B在半圆上,点F、E、B的读数分别为50°、70°、160°,则∠A的度数约为. 14. 如图,抛物线y=ax2+c与直线y=mx+n交于两点A(-2,p),B(5,q),则不等式ax2-mx+c≤n的解集是.
14. 如图,抛物线y=ax2+c与直线y=mx+n交于两点A(-2,p),B(5,q),则不等式ax2-mx+c≤n的解集是. 15. 如图,半圆O的直径AB为15,弦BC为9,弦BD平分∠ABC,则BD的长是.
15. 如图,半圆O的直径AB为15,弦BC为9,弦BD平分∠ABC,则BD的长是. 16. 已知一次函数y1=-x,二次函数y2=x2-2kx+k2-k(k>0).(1)、当x<1时,y2的函数值随x的增大而减小,则k的最小整数值为;(2)、若y=y2-y1 , 若点M(k+2,s),N(a,b)都在函数的y图象上,且s<b,则a的取值范围 . (用含k的式子表示)
16. 已知一次函数y1=-x,二次函数y2=x2-2kx+k2-k(k>0).(1)、当x<1时,y2的函数值随x的增大而减小,则k的最小整数值为;(2)、若y=y2-y1 , 若点M(k+2,s),N(a,b)都在函数的y图象上,且s<b,则a的取值范围 . (用含k的式子表示)三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分,各小题都必须写出解答过程)
-
17. 已知 ,(1)、求;(2)、若2a+b+2c=-30,求a,b,c的值.18. 有一个转盘如图,让转盘自由转动两次,求:
 (1)、第一次指针落在白色区域的概率为.(2)、用画树状图或列表法求指针一次落在白色区域,另一次落在灰色区域的概率.19. 已知二次函数y=2x2-4x-6.(1)、将y=2x2-4x-6化成y=a(x-h)2+k的形式;(2)、写出抛物线的开口方向、对称轴和顶点坐标;(3)、当-1≤x≤2时,直接写出函数y的取值范围.20. 如图,
(1)、第一次指针落在白色区域的概率为.(2)、用画树状图或列表法求指针一次落在白色区域,另一次落在灰色区域的概率.19. 已知二次函数y=2x2-4x-6.(1)、将y=2x2-4x-6化成y=a(x-h)2+k的形式;(2)、写出抛物线的开口方向、对称轴和顶点坐标;(3)、当-1≤x≤2时,直接写出函数y的取值范围.20. 如图,
已知△ABC,∠A=60°
(1)、用尺规作△ABC的外接圆O;(2)、若⊙O的半径为4,求扇形BOC的面积.21. 在2020年新冠肺炎抗疫期间,经营者小明决定在某直销平台上销售一批口罩,经市场调研发现:该类型口罩每袋进价为20元,当售价为每袋25元时,销售量为250袋,销售单价每提高1元,销售量就会减少10袋.(1)、直接写出小明销售该类型口罩的销售量y(袋)与销售单价x(元)之间的函数关系式;(2)、求每天所得销售利润W(元)与销售单价x(元)之间的函数关系式;(3)、若每天销售量不少于200袋,且每袋口罩的销售利润至少为7元,则销售单价定为多少元时,所获利润最大?最大利润是多少?22. 如图,AB为⊙O的直径,点C、D都在⊙O上,且CD平分∠ACB,交AB于点E. (1)、求∠ABD的大小;(2)、若DE=13,AE=17,求⊙O的半径;(3)、DF⊥AC于点F,试探究线段AF、DF、BC之间的数量关系,并说明理由.23. 在平面直角坐标系中,设二次函数y=ax2+bx+2(a,b是常数,a≠0).(1)、若a=2时,图象经过点(1,1),求二次函数的表达式.(2)、写出一组a,b的值,使函数y=ax2+bx+2的图象与x轴只有一个公共点,并求此二次函数的顶点坐标.(3)、已知,二次函数y=ax2+bx+2的图象和直线y=ax+4b都经过点(2,m),求证:a2+b2 .24. 已知:如图1,四边形ABCD内接于O,AC⊥BD于点P,F为BC延长线上一点.
(1)、求∠ABD的大小;(2)、若DE=13,AE=17,求⊙O的半径;(3)、DF⊥AC于点F,试探究线段AF、DF、BC之间的数量关系,并说明理由.23. 在平面直角坐标系中,设二次函数y=ax2+bx+2(a,b是常数,a≠0).(1)、若a=2时,图象经过点(1,1),求二次函数的表达式.(2)、写出一组a,b的值,使函数y=ax2+bx+2的图象与x轴只有一个公共点,并求此二次函数的顶点坐标.(3)、已知,二次函数y=ax2+bx+2的图象和直线y=ax+4b都经过点(2,m),求证:a2+b2 .24. 已知:如图1,四边形ABCD内接于O,AC⊥BD于点P,F为BC延长线上一点.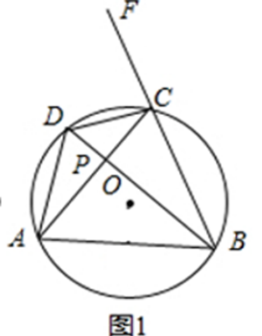
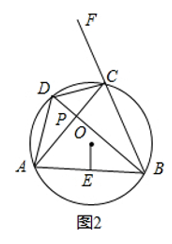
 (1)、求证:∠DCF=∠DAB(2)、过O作OE⊥AB于点E(如图2),试猜想线段OE与DC的数量关系,并证明你的猜想.(3)、当图2中点P运动到圆外时,即AC、BD的延长线交于点P,且∠P=90°时如图所示 , (2)中的猜想是否成立?如果成立请给出你的证明,如果不成立请说明理由.
(1)、求证:∠DCF=∠DAB(2)、过O作OE⊥AB于点E(如图2),试猜想线段OE与DC的数量关系,并证明你的猜想.(3)、当图2中点P运动到圆外时,即AC、BD的延长线交于点P,且∠P=90°时如图所示 , (2)中的猜想是否成立?如果成立请给出你的证明,如果不成立请说明理由.