湖南省娄底市2023-2024学年九年级上学期月考数学试卷(10月)
试卷更新日期:2023-11-17 类型:月考试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列函数中,是的反比例函数的是( )A、 B、 C、 D、2. 如图,点P在反比例函数y= 的图象上,PA⊥x轴于点A,PB⊥y轴于点B,且△APB的面积为2,则k等于( )
 A、-4 B、-2 C、2 D、43. 在同一直角坐标系中,函数与的大致图象可能为( )A、
A、-4 B、-2 C、2 D、43. 在同一直角坐标系中,函数与的大致图象可能为( )A、 B、
B、 C、
C、 D、
D、 4. 某开发公司2021年投入的研发资金为100亿元,为了扩大产品的竞争力,该公司不断增加研发投资,计划2023年投入400亿元研发资金.若2021年到2023年投入的研发资金年平均增长率均为x , 则下列方程中正确的是( )A、100(1+x)=400 B、100(1+2x)=400 C、100(1+x)+100(1+x)2=400 D、100(1+x)2=4005. 若为方程的解,则的值为( )A、 B、 C、 D、6. 已知一元二次方程 , 下列配方正确的是( )A、 B、 C、 D、7. 已知关于的一元二次方程有两个不相等的实数根,则的取值范围是( )A、 B、 C、且 D、且8. 若 , 是方程的两个根,则的值为( )A、 B、 C、 D、9. 已知一个三角形三边长为 , , , 且满足 , , , 则此三角形的形状是( )A、等腰三角形 B、等边三角形 C、直角三角形 D、钝角三角形10. 如图,点是反比例函数与的一个交点,图中阴影部分的面积为 , 则该反比例函数的表达式为( )
4. 某开发公司2021年投入的研发资金为100亿元,为了扩大产品的竞争力,该公司不断增加研发投资,计划2023年投入400亿元研发资金.若2021年到2023年投入的研发资金年平均增长率均为x , 则下列方程中正确的是( )A、100(1+x)=400 B、100(1+2x)=400 C、100(1+x)+100(1+x)2=400 D、100(1+x)2=4005. 若为方程的解,则的值为( )A、 B、 C、 D、6. 已知一元二次方程 , 下列配方正确的是( )A、 B、 C、 D、7. 已知关于的一元二次方程有两个不相等的实数根,则的取值范围是( )A、 B、 C、且 D、且8. 若 , 是方程的两个根,则的值为( )A、 B、 C、 D、9. 已知一个三角形三边长为 , , , 且满足 , , , 则此三角形的形状是( )A、等腰三角形 B、等边三角形 C、直角三角形 D、钝角三角形10. 如图,点是反比例函数与的一个交点,图中阴影部分的面积为 , 则该反比例函数的表达式为( )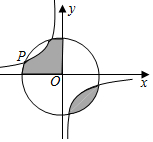 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共8小题,共24.0分)
-
11. 已知y与x成反比例,且当x=-3时,y=4,则当x=6时,y的值为.12. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系是 .13. 如图是函数 , 和在同一个平面直角坐标系中的部分图象,根据图象的位置判断、和间的大小关系为 .
 14. 当三角形的面积为9cm2时,它的底边长a(cm)与底边上的高h(cm)之间的函数表达式为 .15. 方程的解是 .16. 关于的方程的两根分别为 , , 则的值为 .17. 若 , , 则与的大小关系为 .18. 已知 , 是方程的两个实数根,则代数式的值为 .
14. 当三角形的面积为9cm2时,它的底边长a(cm)与底边上的高h(cm)之间的函数表达式为 .15. 方程的解是 .16. 关于的方程的两根分别为 , , 则的值为 .17. 若 , , 则与的大小关系为 .18. 已知 , 是方程的两个实数根,则代数式的值为 .三、解答题(本大题共8小题,共66.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 已知函数 ,(1)、当 , 为何值时是一次函数?(2)、当 , 为何值时,为正比例函数?(3)、当 , 为何值时,为反比例函数?20. 解方程:(1)、;(2)、 .21. 如图,一次函数的图象与反比例函数的图象交于点 , .
 (1)、求反比例函数与一次函数的表达式;(2)、若为轴上一点,的面积为 , 求点的坐标;(3)、结合图象,关于的不等式的解集为 .22. 若 , 是一元二次方程的两个根,求下列式子的值.(1)、;(2)、 .23. 根据物理学知识,在压力不变的情况下,某物体承受的压强是它的受力面积的反比例函数,其函数图象如图所示.
(1)、求反比例函数与一次函数的表达式;(2)、若为轴上一点,的面积为 , 求点的坐标;(3)、结合图象,关于的不等式的解集为 .22. 若 , 是一元二次方程的两个根,求下列式子的值.(1)、;(2)、 .23. 根据物理学知识,在压力不变的情况下,某物体承受的压强是它的受力面积的反比例函数,其函数图象如图所示. (1)、关于的函数关系式为 .(2)、求当时,物体所受的压强是 .(3)、当时,求受力面积的变化范围.24. 已知关于的一元二次方程有两个实数根.(1)、求的取值范围;(2)、设是方程的一个实数根,且满足 , 求的值.
(1)、关于的函数关系式为 .(2)、求当时,物体所受的压强是 .(3)、当时,求受力面积的变化范围.24. 已知关于的一元二次方程有两个实数根.(1)、求的取值范围;(2)、设是方程的一个实数根,且满足 , 求的值.
