甘肃省张掖市高台县部分校联考2023-2024学年九年级上学期月考数学试卷

试卷更新日期：2023-11-17 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列方程中，是关于 $x$ 的一元二次方程的是（）

A、 $a x^{2} + b x + c = 0$ B、 $x^{2} + 1 = 0$ C、 $x^{2} - y - 2 = 0$ D、 $x^{2} - 3 x = x^{2} + 2$

查看试题解析
2. 一元二次方程x²－8x－1＝0配方后可变形为（）

A、（x＋4）²＝17 B、（x＋4）²＝15 C、（x－4）²＝17 D、（x－4）²＝15

查看试题解析
3. 下列图形的性质中，矩形不一定具有的是（）

A、对角线互相垂直平分 B、四个角相等 C、既是轴对称图形，又是中心对称图形 D、对角线互相平分且相等

查看试题解析
4. 根据表格对应值：
$x$
$1.1$
$1.2$
$1.3$
$1.4$
$a x^{2} + b x + c$
$- 0.59$
$0.84$
$2.29$
$3.76$
判断关于 $x$ 的方程 $a x^{2} + b x + c = 3$ 的一个解 $x$ 的范围是（）

A、 $1.1 < x < 1.2$ B、 $1.2 < x < 1.3$ C、 $1.3 < x < 1.4$ D、无法判定

查看试题解析
5. 如图，已知四边形 $A B C D$ 是平行四边形，对角线 $A C 、 B D$ 交于点 $O$ ，则下列结论中错误的是（）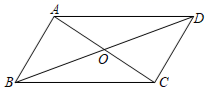

A、当 $A B = B C$ 时，它是菱形 B、当 $∠ A B C = 90 °$ 时，它是正方形 C、当 $A C = B D$ 时，它是矩形 D、当 $A C ⊥ B D$ 时，它是菱形

查看试题解析
6. 不透明的袋子中有两个小球，上面分别写着数字“ $1$ ”，“ $2$ ”，除数字外两个小球无其他差别．从中随机摸出一个小球，记录其数字，放回并摇匀，再从中随机摸出一个小球，记录其数字，那么两次记录的数字之和为 $3$ 的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
7. 若四边形两条对角线相等，则顺次连接其各边中点得到的四边形是（）

A、菱形 B、矩形 C、梯形 D、正方形

查看试题解析
8. 如图：长方形纸片ABCD中，AD＝4cm，AB＝10cm，按如图的方式折叠，使点B与点D重合.折痕为EF，则DE长为（）

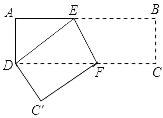A、4.8 cm B、5 cm C、5.8 cm D、6 cm

查看试题解析
9. 共享单车为市民出行带来了方便，某单车公司第一个月投放1000辆单车，计划第三个月投放单车数量比第一个月多440辆．设该公司第二、三两个月投放单车数量的月平均增长率为x，则所列方程正确的为（）

A、1000（1+x）²=1000+440 B、1000（1+x）²=440 C、440（1+x）²=1000 D、1000（1+2x）=1000+440

查看试题解析
10. 如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE=DF；②∠DAF=15°；③AC垂直平分EF；④BE+DF=EF；⑤S_△CEF=2S_△ABE ，其中正确结论有（）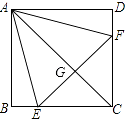

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题（本大题共8小题，共32.0分）

11. 已知关于 $x$ 的方程 $x^{2} + 5 x + m = 0$ 的一根为 $- 1$ ，则方程的另一根为．

查看试题解析
12. 在一个不透明的袋子里有50个除颜色外均相同的小球，每次摸球前先将盒中的球摇匀，随机摸出一个球记下颜色后再放回盒中，通过大量重复实验后，发现摸到红球的频率稳定在0.4，由此估计袋中红球的个数为．

查看试题解析
13. 已知关于x的一元二次方程(k＋1)x²－2x＋1＝0有实数根，则k的取值范围是.

查看试题解析
14. 如图，四边形 $A B C D$ 是正方形，延长 $A B$ 到点 $E$ ，使 $A E = A C$ ，则 $∠ B C E$ 的度数是。

查看试题解析
15. 如图，菱形ABCD的对角线AC、BD相交于点O，且AC=8，BD=6，过点O作OH丄AB，垂足为H，则点0到边AB的距离OH= ．

查看试题解析
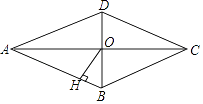16. 扬州某毛绒玩具厂对一批毛绒玩具进行抽检的结果如下：
抽取的毛绒玩具数 $n$
$20$
$50$
$100$
$200$
$500$
$1000$
$1500$
$2000$
优等品的频数 $m$
$19$
$47$
$91$
$184$
$462$
$921$
$1379$
$1846$
优等品的频率 $\frac{m}{n}$
$0.950$
$0.940$
$0.910$
$0.920$
$0.924$
$0.921$
$0.919$
$0.923$
从这批玩具中，任意抽取的一个毛绒玩具是优等品的概率的估计值是 $. ($ 精确到 $0.01)$

查看试题解析
17. 设x₁ ， x₂是一元二次方程x²-3x-2=0的两个实数根，则x₁²+3x₁x₂+x₂²的值为．

查看试题解析
18. 在一幅长 $80 c m$ ，宽 $50 c m$ 的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示．如果要使整个挂图的面积是 $5400 c m^{2}$ ，设金色纸边的宽为 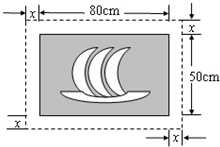$x c m$ ，则可列方程．

查看试题解析

三、解答题（本大题共8小题，共88.0分。解答应写出文字说明，证明过程或演算步骤）

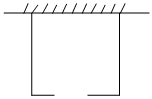
19. 按要求解下列方程：

(1)、 $2 x^{2} - x - 1 = 0$ ； $($ 用配方法解 $)$

(2)、 $2 x^{2} - 7 x + 6 = 0$ ； $($ 用公式法解 $)$

(3)、 $2 y^{2} + 4 y = y + 2$ ； $($ 用因式分解法解 $)$

(4)、 $5 x + 2 = 3 x^{2}$ ．

查看试题解析
20. 附中现要从甲、乙两位男生和丙、丁两位女生中，选派两位同学分别作为 $①$ 号选手和 $②$ 号选手代表学校参加全市汉字听写大赛．

(1)、请用树形图或列表法列举出各种可能选派的结果；

(2)、求恰好选派一男一女两位同学参赛的概率．

查看试题解析
21. 已知关于 $x$ 的方程 $x^{2} - (m + 2) x + (2 m - 1) = 0$ ．

(1)、求证：方程恒有两个不相等的实数根．

(2)、若此方程的一个根是 $1$ ，请求出方程的另一个根，并求以此两根为边长的直角三角形的面积．

查看试题解析
22. 在“乡村振兴”行动中，某村办企业开发了一种成本价为50元/盒的有机产品，如果每盒的售价为60元时，每天可以销售200盒，通过市场调查发现，每盒售价每提高1元，每天少卖出10盒．该村办企业要想每天获得2240元利润，该有机产品的售价可以定为多少元/盒？

查看试题解析
23. 学校计划利用一块空地修建一个学生自行车棚，其中一面靠墙，这堵墙的长度为 $12$ 米，建造车棚的面积为 $80$ 平方米 $.$ 已知新建板墙的木板材料的总长为 $26$ 米 $.$ 为了方便学生出行，学校决定在与墙平行的一面开一个 $2$ 米宽的门，那么车棚的长与宽分别为多少米？

查看试题解析
24. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D ⊥ B C$ ，垂足为点 $D$ ， $A N$ 是 $△ A B C$ 外角 $∠ C A M$ 的平分线， $C E ⊥ A N$ ，垂足为点 $E$ ．

(1)、求证：四边形 $A D C E$ 为矩形；

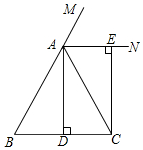(2)、当 $△ A B C$ 满足什么条件时，四边形 $A D C E$ 是一个正方形？请给出证明．

查看试题解析
25. 如图，在四边形 $A B C D$ 中， $A D / / B C$ ，对角线 $B D$ 的垂直平分线与边 $A D$ 、 $B C$ 分别相交于点 $M$ 、 $N$ ．

(1)、求证：四边形 $B N D M$ 是菱形；

(2)、若 $B D = 24$ ， $M N = 10$ ，求菱形 $B N D M$ 的周长．

查看试题解析
26. 如图，在矩形 $A B C D$ 中， $A B = 3 c m$ ， $B C = 6 c m .$ 点 $P$ 从点 $D$ 出发向点 $A$ 运动，运动到点 $A$ 即停止；同时，点 $Q$ 从点 $B$ 出发向点 $C$ 运动，运动到点 $C$ 即停止，点 $P$ 、 $Q$ 的速度都是 $1 c m / s .$ 连接 $P Q$ 、 $A Q$ 、 $C P .$ 设点 $P$ 、 $Q$ 运动的时间为 $t s$ ．

(1)、当 $t$ 为何值时，四边形 $A B Q P$ 是矩形，请说明理由；

(2)、当 $t$ 为何值时，四边形 $A Q C P$ 是菱形，请说明理由；

(3)、直接写出 $(2)$ 中菱形 $A Q C P$ 的周长和面积，周长是 $c m$ ，面积是 $c m^{2}$ ．

查看试题解析

$x$	$1.1$	$1.2$	$1.3$	$1.4$
$a x^{2} + b x + c$	$- 0.59$	$0.84$	$2.29$	$3.76$

抽取的毛绒玩具数 $n$	$20$	$50$	$100$	$200$	$500$	$1000$	$1500$	$2000$
优等品的频数 $m$	$19$	$47$	$91$	$184$	$462$	$921$	$1379$	$1846$
优等品的频率 $\frac{m}{n}$	$0.950$	$0.940$	$0.910$	$0.920$	$0.924$	$0.921$	$0.919$	$0.923$