河北省石家庄市赵县2023-2024学年九年级上学期月考数学试卷（9月份）

试卷更新日期：2023-11-17 类型：月考试卷

进入出卷网下载

一、选择题（本大题共16小题，共38.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列函数是二次函数的是（）

A、 $y = \frac{1}{x^{2}}$ B、 $y = x - 1$ C、 $y = 3 x^{2} + 6 x - 2$ D、 $y = (x - 3)^{2} - x^{2}$

查看试题解析
2. 若抛物线 $y = a x^{2} + 4 x + 5$ 的开口向下，则 $a$ 的值可以是（）

A、 $0$ B、 $1$ C、 $2$ D、 $- 2$

查看试题解析
3. 若 $(a + 1) x^{| a - 1 |} - 4 = 0$ 是关于 $x$ 的一元二次方程，则 $a$ 的值为（）

A、 $3$ B、 $- 1$ C、 $0$ D、 $3$ 或 $- 1$

查看试题解析
4. 将一元二次方程 $2 x^{2} = 5 x - 3$ 化成一般形式之后，若二次项的系数是 $2$ ，则一次项系数和常数项分别为（）

A、 $5$ ， $- 3$ B、 $- 5$ ， $- 3$ C、 $5$ ， $3$ D、 $- 5$ ， $3$

查看试题解析
5. 老师设计了一个用合作的方式完成配方法解一元二次方程的接力游戏，规则如下：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后解出方程，过程如图所示，老师看后，发现有一位同学负责的步骤是错误的，这位同学是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 二次函数 $y = 2 x^{2} - 3 x + □$ 的图象与 $x$ 轴有两个交点，则“ $□$ ”表示的数可以是（）

A、 $1$ B、 $\frac{9}{8}$ C、 $2$ D、 $3$

查看试题解析
7. 某药品经过连续两次降价后，每盒的零售价由 $40$ 元降为 $25.6$ 元，若两次降价的百分率相等，则降价的百分率为（）

A、 $10 %$ B、 $20 %$ C、 $25 %$ D、 $30 %$

查看试题解析
8. 在平面直角坐标系中，将二次函数 $y = (x + 1)^{2} - 2$ 的图象向右平移 $2$ 个单位长度，再向上平移 $1$ 个单位长度，所得函数的解析式为（）

A、 $y = (x + 3)^{2} - 3$ B、 $y = (x - 1)^{2} - 1$ C、 $y = (x + 3)^{2} - 1$ D、 $y = (x - 1)^{2} - 3$

查看试题解析
9. 在平面直角坐标系中，对于二次函数 $y = x^{2} + 2 x - 3$ ，下列说法中错误的是（）

A、函数图象的顶点坐标为 $(- 1 ， - 4)$ B、 $y$ 的最小值为 $- 3$ C、函数图象与坐标轴有三个交点 D、当 $x < - 1$ 时， $y$ 随 $x$ 的增大而减小

查看试题解析

10. 某节数学课上，老师让学生解关于

x

的方程

x (x + 5) = 2 (x + 5)

，下面是三位同学的解答过程：

小逸

小明

小琛

两边同时除以 $(x + 5)$ ，得 $x = 2$ ．

整理得 $x^{2} + 3 x = 10$ ，

配方得 $x^{2} + 3 x + \frac{9}{4} = 10 + \frac{9}{4}$ ，

$∴ (x + \frac{3}{2})^{2} = \frac{49}{4}$ ，

$∴ x + \frac{3}{2} = \pm \frac{7}{2}$ ，

$∴ x_{1} = 2$ ， $x_{2} = - 5$ ．

移项得 $x (x + 5) - 2 (x + 5) = 0$ ，

$∴ (x + 5) (x - 2) = 0$ ，

$∴ x + 5 = 0$ 或 $x - 2 = 0$ ，

$∴ x_{1} = - 5 . x_{2} = 2$ ．

下列选项中说法正确的是（）

A、只有小明的解法正确 B、只有小琛的解法正确 C、只有小逸的解法错误 D、小逸和小琛的解法都是错误的

查看试题解析

11. 已知抛物线 $y = a x^{2} - 4 a x + c$ 经过点 $(- 1 ， 2)$ ，则该抛物线必然还经过点（）

A、 $(- 1 ， - 2)$ B、 $(- 3 ， 2)$ C、 $(3 ， 2)$ D、 $(5 ， 2)$

查看试题解析
12. 一个弹性球从地面竖直向上弹起时的速度为 $6$ 米 $/$ 秒，经过 $t$ 秒时，球距离地面的高度 $h ($ 米 $)$ 满足公式 $h = 6 t - 5 t^{2}$ ，那么球弹起后又回到地面所花的时间 $t$ 是（）

A、 $0.6$ B、 $1$ C、 $1.2$ D、 $2$

查看试题解析
13. 已知 $x_{1}$ ， $x_{2}$ 是一元二次方程 $x^{2} - 2 x - 1 = 0$ 的两根，则 $x_{1}^{2} + x_{2}^{2}$ 的值是（）

A、 $6$ B、 $2$ C、 $- 2$ D、 $4$

查看试题解析
14. 我国古代著作 $《$ 四元玉鉴 $》$ 记载“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽．每株脚钱三文足，无钱准与一株椽．”其大意为：现请人代买一批椽，这批椽的价钱为 $6210$ 文．如果每株椽的运费是 $3$ 文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问 $6210$ 文能买多少株椽？设这批椽的数量为 $x$ 株，则符合题意的方程是（）

A、 $3 (x + 1) x = 6210$ B、 $3$ $(x - 1) = 6210$ C、 $(3 x - 1) x = 6210$ D、 $3 (x - 1) x = 6210$

查看试题解析
15. 如图，这是一块直径为 $a + b$ 的圆形钢板，从中挖去直径分别为 $a$ 和 $b$ 的两个圆，当 $a + b = 4$ 时，剩下的钢板面积的最大值是（）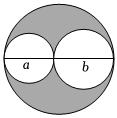

A、 $π$ B、 $2 π$ C、 $4 π$ D、 $6 π$

查看试题解析
16. 嘉琪同学在研究二次函数 $y = - (x - h)^{2} - h + 1 (h$ 为常数 $)$ 的性质时得到以下结论： $①$ 这个函数图象的顶点始终在直线 $y = - x + 1$ 上； $②$ 当 $- 2 < x < 1$ 时， $y$ 随 $x$ 的增大而减小，则 $h$ 的取值范围为 $h \leq - 2$ ； $③$ 点 $A (x_{1} ， y_{1})$ 与点 $B (x_{2} ， y_{2})$ 在函数图象上，若 $| x_{1} - h | > | x_{2} - h |$ ，则 $y_{1} < y_{2}$ ； $④$ 存在一个 $h$ 的值，使得函数图象与 $x$ 轴的两个交点和函数图象的顶点构成等腰直角三角形 $.$ 其中正确的结论有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析

二、填空题（本大题共3小题，共10.0分）

17. 已知关于 $x$ 的方程 $x^{2} + a x - 8 = 0$ 的一个根是 $- 2$ ，则 $a$ 的值是．

查看试题解析
18. 已知抛物线 $y = (a - 1) x^{2} - 2 x + a^{2} - 1$ ，若该抛物线的开口向上，则 $a$ 的取值范围为；若抛物线经过原点，则 $a =$ ．

查看试题解析
19. 如图，这是抛物线 $y = (x - h)^{2} - 9$ 的部分图象，则 $h =$ ；若 $y \leq 0$ ，则自变量 $x$ 的取值范围是．

查看试题解析

三、解答题（本大题共7小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）

20. 请用适当的方法解一元二次方程．

(1)、 $x^{2} - 4 x - 1 = 0$ ；

(2)、 $2 x^{2} + 3 x - 1 = 0$ ．

查看试题解析
21. 已知抛物线 $y = (x + 3)^{2} - 1$ ，点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 落在抛物线上，且满足 $- 3 < x_{1} < x_{2}$ ．

(1)、请比较 $y_{1}$ 与 $y_{2}$ 的大小．

(2)、抛物线经过怎样的变换，可以使其顶点与原点重合？ $($ 只写出一种平移方式即可 $)$

查看试题解析
22. 已知一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ．

(1)、若满足 $a - b + c = 0$ ，则方程必有一个根为．

(2)、若 $a$ ， $b$ ， $c$ 满足 $\sqrt{a - 1} + | b - 2 | + (c + 3)^{2} = 0$ 求一元二次方程的根．

查看试题解析
23. 某纪念品的进价为每件 $40$ 元，售价为每件 $50$ 元，每星期可卖出 $200$ 个 $.$ 经市场调查发现：以不低于现售价的价格销售该商品，售价每上涨 $1$ 元，则每星期少卖 $4$ 个 $($ 每件售价不高于 $68$ 元 $)$ ，设每件商品销售单价为 $x ($ 元 $)$ ，每星期销售量为 $y ($ 个 $)$ ．

(1)、求 $y$ 与 $x$ 之间的函数关系式，并直接写出自变量 $x$ 的取值范围；

(2)、将该纪念品的销售单价定为多少元时，每星期销售这种产品获得的利润最大？最大利润是多少元？

查看试题解析
24. 已知关于 $x$ 的方程 $m x^{2} + (3 m - 4) x - 12 = 0$ ．

(1)、求证：无论 $m$ 取何值，方程总有实数根．

(2)、若方程的根为整数，求 $m$ 的值．

查看试题解析
25. 在平面直角坐标系中，已知抛物线 $y = a x^{2} - 4 a x + 1 (a > 0)$ ．

(1)、若抛物线过点 $A (- 1 ， 6)$ ，求该抛物线的解析式．

(2)、若当 $0 \leq x \leq 5$ 时， $y$ 的最小值是 $- 1$ ，则当 $0 \leq x \leq 5$ 时，求 $y$ 的最大值．

(3)、已知直线 $y = - 2 x + 1$ 与抛物线 $y = a x^{2} - 4 a x + 1$ 存在两个交点，若两交点到 $x$ 轴的距离相等，求 $a$ 的值．

查看试题解析
26. 将小球 $($ 看作一点 $)$ 从距离地面 $3 m$ 高的点 $A$ 处向右发射，建立如图所示的平面直角坐标系，小球沿抛物线 $y = - \frac{1}{4} x^{2} + b x + c$ 运动．

(1)、若当小球运动的水平距离为 $1 m$ 时，小球达到最大高度．
$①$ 求小球达到的最大高度；
$②$ 当小球前方无障碍物时，求小球落地时的水平距离．

(2)、若小球的正前方 $4 m (O C = 4 m)$ 处有一个截面为长方形的球筐 $C D E F$ ，其中长 $C D$ 为 $2 m$ ，宽 $D E$ 为 $1 m$ ，若要使小球落入筐中，求 $b$ 的取值范围．

查看试题解析