浙江省金华市兰溪八中2023-2024学年九年级第一学期数学能力调查（一）试卷

试卷更新日期：2023-11-16 类型：月考试卷

进入出卷网下载

一、单选题(本题有10小题，每小题3分，共30分)

1. ﹣ $\frac{5}{4}$ 的相反数是（）

A、﹣ $\frac{4}{5}$ B、 $\frac{5}{4}$ C、﹣ $\frac{5}{4}$ D、 $\frac{4}{5}$

查看试题解析
2. 电影《满江红》备受观众喜爱，截止到2023年3月初，累计票房45.39亿元，45.39亿用科学记数法表示为（）

A、4.539×10⁷ B、45.39×10⁸ C、4.539×10⁹ D、4.539×10¹⁰

查看试题解析
3. 已知⊙O的半径为6，点P到圆心O的距离为4，则点P在（）

A、⊙O内 B、⊙O外 C、⊙O上 D、无法确定

查看试题解析
4. 以原点为中心，将点P（4，5）按逆时针方向旋转90°，得到的点Q所在的象限为（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 张婷同学将一根绳子进行黄金分割，分割后较短绳子的长度为 $(3 - \sqrt{5})$ 米，则分割前这根绳子的总长度为（）

A、1米 B、1.5米 C、2米 D、4米

查看试题解析
6. 如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD＝55°，则∠BCD的度数为（）

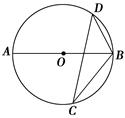A、35° B、45° C、55° D、75°

查看试题解析
7. 由 $y = x^{2}$ 平移得到抛物线 $y = {(x + 1)}^{2} - 2$ ，则下列平移过程正确的是（）

A、先向左平移1个单位，再向上平移2个单位 B、先向左平移1个单位，再向下平移2个单位 C、先向右平移1个单位，再向下平移2个单位 D、先向右平移1个单位，再向上平移2个单位

查看试题解析
8. 如图，⊙O的周长等于4πcm，则它的内接正六边形ABCDEF的面积是（　　）

A、 $\sqrt{3}$ B、 $3 \sqrt{3}$ C、 $6 \sqrt{3}$ D、 $12 \sqrt{3}$

查看试题解析
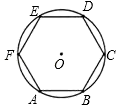9. 已知二次函数 $y = 2 x^{2} - 8 x + 9$ ，当 $1 \leq x \leq 5$ 时，函数 $y$ 的最大值为（）

A、1 B、3 C、9 D、19

查看试题解析
10. 已知二次函数y=ax²+bx+c（a、b、c都是常数，且a≠0）的图象与x轴交于点（﹣2，0）、（x₁ ， 0），且1＜x₁＜2，与y轴交于正半轴，且交点在（0，2）的下方，下列结论①4a﹣2b+c=0； ②a＜b＜0；③2a+c＞0；④2a﹣b+1＞0．其中正确结论的个数是（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题(本题有6小题，每小题4分，共24分)

11. 使 $\frac{\sqrt{x - 1}}{3}$ 在实数范围内有意义的x的取值范围是.

查看试题解析
12. 如果一个扇形的半径是1，弧长是 $\frac{π}{3}$ ，那么此扇形的圆心角的大小为度.

查看试题解析
13. 如图，AB是⊙O的弦，AB＝4，点C是⊙O上的一个动点，且∠ACB＝45°.若点M，N分别是AB，BC的中点，则MN长的最大值是.

查看试题解析
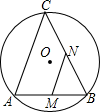14. 如图，在▱ABCD中，点E在DC边上，若 $\frac{D E}{E C} = \frac{1}{2}$ ，则 $\frac{B F}{E F}$ 的值为.

查看试题解析
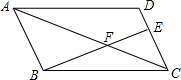15. 已知，AB，CD是⊙O中的两条弦，且AB∥CD。圆的半径为10，AB=12，CD=16，则AB与CD之间的距离是

查看试题解析
16. 定义：在平面直角坐标系中，我们将横、纵坐标都是整数的点称为“整点”.若抛物线y＝ax²﹣2ax+a+3与x轴围成的区域内(不包括抛物线和x轴上的点)恰好有8个“整点”，则a的取值范围是.

查看试题解析

三、解答题(本题有8小题，共66分，各小题都必须写出解答过程)

17. 先化简后求值：（2x+y）²﹣3x（x+y）﹣（x﹣2y）（x+2y），其中x＝ $\frac{1}{2}$ ， y＝﹣2．

查看试题解析
18. 在一个不透明的盒子里有红球、黄球、绿球各一个，它们除了颜色外其余都相同，小颖从盒子里随机摸出一球，记录下颜色后放回盒子里，充分摇匀后，再随机摸出一球，并记录下颜色．请用列表法或画树状图法，求小颖两次摸出的球颜色相同的概率．

查看试题解析
19. 一次函数 $y_{1} = k x + b$ 与反比例函数 $y_{2} = \frac{n}{x} (n > 0)$ 交于点 A (1，3)，B (3，m)，

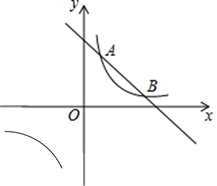(1)、分别求两个函数的解析式；

(2)、根据图像直接写出，当x为何值时， $y_{1} < y_{2}$ ；

查看试题解析
20. 如图，已知△ABC是⊙O的内接三角形，AD是⊙O的直径，连结BD，BC平分∠ABD.

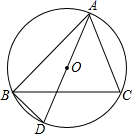(1)、求证：∠CAD=∠ABC；

(2)、若AD=6，求 $\overset{⌢}{C D}$ 的长.

查看试题解析
21. 在△ABC中，AB=AC，在BC上取点E，连结AE并延长至点D，使得∠D=∠C．

(1)、求证：△ABE∽△ADB．

(2)、若DE=1，AE=5，求AC的长.

查看试题解析
22. “新冠肺炎”疫情期间某工厂为支持国家抗击疫情每天连夜生产急缺的消毒液，已知每瓶消毒液的生产成本为20元，为了合理定价，根据市场调查发现，当销售单价为30元时，每天的销售量为6000瓶，若销售单价每降低1元，则每天能多销售1000瓶，但要求销售单价不能低于成本且不高于30元.

(1)、求每天的销售量 $y$ （瓶）与销售单价 $x$ （元）之间的函数关系式；

(2)、求每天的利润 $w$ （元）与销售单价 $x$ （元）之间的函数关系式；

(3)、该工厂负责人决定将每天的利润全部捐献出来进一步支持国家抗击“新冠肺炎”疫情，则当销售单价为多少元时，每天的销售利润最大？最大利润是多少？

查看试题解析
23.
【问题呈现】
已知， $△ C A B$ 和 $△ C D E$ 都是直角三角形， $∠ A C B = ∠ D C E = 90 ° ， C B = m C A ， C E = m C D$ ，连接 $A D$ ， $B E$ ，探究 $A D$ ， $B E$ 的位置关系．

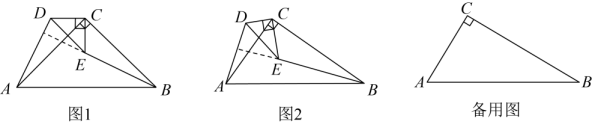(1)、如图1，当 $m = 1$ 时，直接写出 $A D$ ， $B E$ 的位置关系：；

(2)、如图2，当 $m \neq 1$ 时，（1）中的结论是否成立？若成立，给出证明；若不成立，说明理由．

(3)、【拓展应用】
当 $m = \sqrt{3} ， A B = 4 \sqrt{7} ， D E = 4$ 时，将 $△ C D E$ 绕点C旋转，使 $A ， D ， E$ 三点恰好在同一直线上，求 $B E$ 的长．

查看试题解析
24. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与x轴交于A，B两点，与y轴交于点C. $A C = \sqrt{1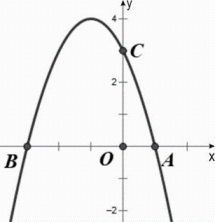0}$ ， OB=OC=3OA.

(1)、求抛物线的解析式；

(2)、在第二象限内的抛物线上确定一点P，使 $Δ P C B$ 的面积最大，求出点P的坐标；

(3)、在（2）的结论下，点M为x轴上一动点，抛物线上是否存在一点Q，使点P，B，M，Q为顶点的四边形是平行四边形，若存在，请求出点Q的坐标；若不存在，请说明理由。

查看试题解析